"Чтение мыслей" по спичкам

Третье видоизменение того же фокуса представляет собой своеобразный способ отгадывания задуманного числа по спичкам. Загадавший должен мысленно делить задуманное число пополам, полученную половину - опять пополам и т. д. (от нечетного числа отбрасывая единицу), и при каждом делении класть перед собой спичку, направленную вдоль стола, если делится число четное, и поперек, если приходится делить нечетное. К концу операции получается фигура вроде показанной на рисунке.

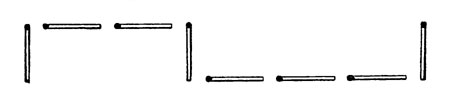
Отгадывание задуманного числа по спичкам: что делает загадывающий

Вы всматриваетесь в эту фигуру и безошибочно называете задуманное число: 137.

Как вы узнаете его?

Способ станет ясен сам собой, если в выбранном примере (137) последовательно обозначить возле каждой спички то число, при делении которого она была положена (см. рисунок).

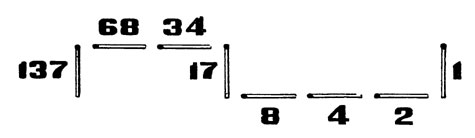
Секрет фокуса: что делает отгадчик

Теперь понятно, что последняя спичка во всех случаях означает число 1, и не составляет труда, восходя от нее к предшествующим делениям, добраться до первоначально задуманного числа. Например, по фигуре рисунка вы можете вычислить, что задумано было число 664. В самом деле, выполняя последовательно удвоения (начиная с конца) и не забывая прибавлять, где надо, единицу, получаем задуманное (см. рисунок).

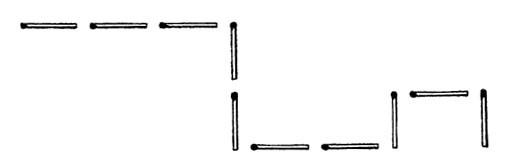
Какое число здесь изображено?

Таким образом, пользуясь спичками, вы прослеживаете ход чужих мыслей, восстанавливаете всю цепь выкладок.

Тот же результат мы можем получить иначе, сообразив, что лежащая спичка должна соответствовать в двоичной системе нолю (деление на 2 без остатка), а стоящая - единице.

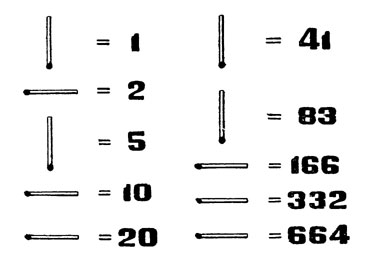
Ответ на вопрос предыдущего рисунка

Таким образом, в первом примере мы имеем (читая справа налево) число:

   1   0    0    0  1  0   0  1 
 128 (64) (32) (16) 8 (4) (2) 1

или в десятичной системе:

128 + 8 + 1 = 137.

А во втором примере задуманное число изображается по двоичной системе так:

   1    0    1   0    0   1 1  0   0   0 
 512 (256) 128 (64) (32) 16 8 (4) (2) (1)

или по десятичной системе:

512 + 128 + 16 + 8 = 664. 

Попробуйте решить, какое число задумано, если получилась фигура (см. рис.).

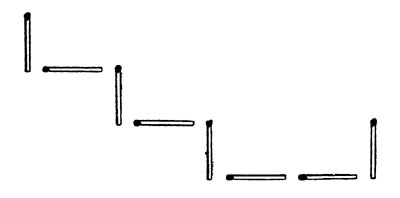
Какое число изображено этой фигурой?

Решение будет такое.

Число "10010101" в двоичной системе соответствует в десятичной:

128 + 16 + 4 + 1 = 149.

Необходимо заметить, что получаемая при последнем делении единица также должна быть отмечаема стоящей спичкой.