Идеальный разновес

У некоторых читателей, вероятно, возник уже вопрос, почему для выполнения описанных раньше опытов мы пользуемся именно двоичной системой? Ведь каждое число можно изобразить в любой системе, между прочим и в десятичной. Чем же объясняется предпочтение здесь двоичной?

Объясняется оно тем, что в этой системе, кроме ноля, употребляется всего одна цифра - единица, а следовательно, число составляется из различных степеней 2, взятых только по одному разу. Если бы в фокусе с кошельками мы распределили деньги, например, по пятеричной системе, то могли бы составить, не раскрывая кошельков, любую сумму лишь в том случае, когда каждый из кошельков повторялся бы у нас не менее 4 раз (в пятеричной системе употребляются ведь, кроме ноля, четыре цифры).

Впрочем, бывают случаи, когда для подобных надобностей удобнее пользоваться не двоичной, а троичной системой, несколько видоизмененной. Сюда относится знаменитая старинная "задача о гирях", которая может послужить сюжетом и для арифметического фокуса.

Представьте, что вам предложили придумать набор из четырех гирь, с помощью которых возможно было бы отвесить любое целое число килограммов, от 1 до 40. Двоичная система подсказывает вам набор:

1 кг, 2 кг, 4 кг, 8 кг, 16 кг,

которым можно отвешивать все грузы от 1 до 31 кг. Но это, очевидно, не удовлетворяет требуемым условиям ни по числу гирь, ни по предельному грузу (31 кг вместо 40). С другой стороны, вы не использовали здесь возможности класть гири не только на одну чашку весов, но и на две, то-есть обходиться не только суммой гирь, но и их разностью. Последнее дает так много разнообразных комбинаций, что вы совершенно теряетесь в поисках, не умея уложить их в какую-либо систему.

Если вам не посчастливится напасть на правильный путь, вы готовы будете даже сомневаться вообще в разрешимости задачи столь малым числом гирь, как четыре.

Посвященный выходит из этого затруднения с волшебной простотой, намечая следующие четыре гири:

1 кг, 3 кг, 9 кг, 27 кг. 

Любое целое число килограммов, до 40 кг, вы можете отвесить такими гирями, кладя их то на одну, то на обе чашки весов. Не приводим примеров, потому что каждый легко может сам убедиться в полной пригодности такого набора гирь для нашей цели. Остановимся лучше на том, почему именно указанный ряд обладает этим свойством. Вероятно, читатели уже заметили, что числа эти - ряд степеней^* числа 3:

30, 31 32, 33.

^* (Единицу можно рассматривать как нулевую степень 3 (вообще - как нулевую степень любого числа).)

Это значит, что мы обращаемся здесь к услугам троичной системы счисления. Гири - цифры этой троичной системы. Но как воспользоваться ею, когда требуемый вес получается в виде разности двух гирь? И как избегнуть необходимости обращаться к удвоению гирь (в троичной системе ведь, кроме ноля, употребляются две цифры: 1 и 2)?

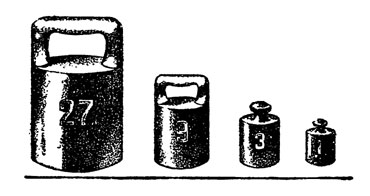
Набор гирь, с помощью которых можно взвесить любой груз от 1 до 40 кг

То и другое достигается введением "отрицательных" цифр. Дело сводится попросту к тому, что вместо цифры 2 употребляют 3 - 1, то-есть единицу высшего разряда, от которой отнимается одна единица низшего. Например, число 2 в нашей видоизмененной троичной системе обозначается не 2, а 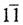, где знак минус над цифрой единиц означает, что единица эта не прибавляется, а отнимается. Точно так же число 5 изобразится не 12, a 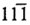(то-есть 9 - 3 - 1 = 5).

Теперь ясно, что если любое число можно изобразить в троичной системе с помощью ноля (то-есть знака отсутствия числа) и одной только цифры, именно прибавляемой или отнимаемой единицы, то из чисел 1, 3, 9, 27 можно, складывая или вычитая их, составить все числа от 1 до 40. Мы как бы пишем все эти числа, употребляя гири вместо цифр. Случай сложения отвечает при взвешивании случаю, когда гири помещаются все на одну чашку, а случай вычитания - когда часть гирь кладется на чашку с товаром и, следовательно, вес ее отнимается от веса остальных гирь. Ноль соответствует отсутствию гири.

Как известно, система эта на практике не употребляется. Всюду в мире, где введена метрическая система мер, применяется набор в 1, 2, 2, 5 единиц, а не 1,3, 9, 27, хотя первым можно отвешивать грузы только до 10 единиц, а вторым - до 40. Не применялся набор 1, 3, 9, 27 и тогда, когда метрическая система еще не была введена. В чем же причина отказа на практике от этого, казалось бы, совершенного разновеса?

Причина кроется в том, что идеальный разновес удобен лишь на бумаге, на деле же пользоваться им весьма хлопотливо. Если бы приходилось только отвешивать заданное число весовых единиц - например, отвесить 400 г масла или 2500 г сахару, - то системой гирь в 100, 300, 900, 2700 можно было бы на практике пользоваться (хотя и тут приходилось бы каждый раз долго подыскивать соответствующую комбинацию). Но когда приходится определять, сколько весит данный товар, то подобный разновес оказывается крайне неудобным: здесь нередко, ради прибавления к поставленным гирям одной единицы, пришлось бы производить полную замену прежней комбинации другой, новой. Отвешивание становится при таких условиях делом крайне медленным и притом утомительным.

Не всякий быстро сообразит, что, например, вес 19 кг получится, если на одну чашку поставить гири в 27 кг и 1 кг, а на другую 9 кг; вес 20 кг - если на одну чашку поставить гири в 27 кг и 3 кг, а на другую - 9 кг и 1 кг. При каждом отвешивании приходилось бы решать подобные головоломки. Разновес 1, 2, 2, 5 таких затруднений не доставляет.