Предсказать сумму ненаписанных чисел

Что можно сказать о человеке, который напишет сумму раньше, чем ему будут названы все слагаемые?

Это, конечно, фокус, и выполняется он в таком виде. Отгадчик предлагает вам написать какое-нибудь многозначное число по вашему выбору. Бросив взгляд на это первое слагаемое, отгадчик пишет на бумажке сумму всей будущей колонны слагаемых и передает вам на хранение. После этого он просит вас (или кого-нибудь из присутствующих) написать еще одно слагаемое - опять какое угодно. А сам затем быстро пишет третье слагаемое. Вы складываете все три написанных числа-и получается как раз тот результат, который заранее был написан отгадчиком на спрятанной у вас бумажке.

Если, например, вы написали в первый раз 83267, то отгадчик пишет будущую сумму 183266. Затем вы пишете, допустим, 27935, а отгадчик приписывает третье слагаемое 72064:

Получается в точности предсказанная сумма, хотя отгадчик не мог знать, каково будет второе слагаемое. Отгадчик может предсказать также сумму пяти или семи слагаемых, но тогда он сам пишет два или три из них. Никакой подмены бумажки с результатом здесь заподозрить вы не можете, так как она до последнего момента хранится в вашем собственном кармане. Очевидно, отгадчик пользуется каким-то неизвестным вам свойством чисел. Каким?

Он пользуется тем, что от прибавления, скажем, к пятизначному числу числа из 5 девяток (99999) это число увеличивается на 100000 - 1, то-есть впереди него появляется единица, а последняя цифра уменьшается на единицу. Например:

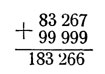
Эту сумму, то-есть сумму написанного вами числа и 99999, отгадчик и пишет на бумажке как будущий результат сложения. А чтобы результат оправдался, он, увидев ваше второе слагаемое, выбирает свое, третье слагаемое так, чтобы вместе со вторым оно составило 99999, то-есть вычитает каждую цифру второго слагаемого из 9. Эти операции вы легко можете теперь проследить на предыдущем примере, а также и на следующих

Легко усмотреть, что вы сильно затрудните отгадчика, если второе ваше слагаемое будет заключать больше цифр, чем первое: отгадчик не сможет написать слагаемое, которое уменьшит второе число для оправдания предсказанного слишком малого результата. Поэтому опытный отгадчик предусмотрительно ограничивает свободу выбора этим условием.

Фокус выходит внушительнее, когда в придумывании слагаемых участвуют несколько лиц. После первого же слагаемого - например, 437 692 - отгадчик уже предсказывает сумму всех пяти чисел, именно записывает 2437690 (здесь будет добавлено дважды 999 999, то-есть 2000000 - 2). Дальнейшее ясно из схемы:

Еще пример:

Читателям небезинтересно будет теперь познакомиться с тем, как описан тот же фокус советским писателем Шишковым в его романе "Странники":

"Иван Петрович вырвал из блокнота страничку, подал мальчонке, спросил:

- Карандаш есть?.. Пиши любое число.

Мальчонка написал. Иван Петрович мельком взглянул на это число, написал на отдельном клочке бумаги

свое какое-то число, сунул бумажку в солому и прикрыл шляпой.

- Пиши под ним другое. Написал?.. Теперь я сам напишу третье. Теперь все три числа складывай. Только тщательней, не ври.

Через две минуты был готов проверенный ответ. Инженер Вошкин (прозвище мальчика. - Я. П.) подал свои выкладки:

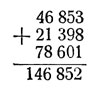
- Сто сорок шесть тысяч восемьсот пятьдесят два, Иван Петрович.

- Долго считаешь. А у меня - вот он ответ. Я уже знал его, когда ты еще первое число написал. Вот. Тяни из-под шляпы.

Мальчонка выхватил бумажку. Там значилось: "146852".

В романе фокус оставляется неразъясненным. Но вам, конечно, вполне понятна его несложная арифметическая основа.