Глава 3. Удивительные функции и линии, или прогулки по математической кунсткамере

Общий фундамент. Через всю историю развития математической науки проходят диалектические противоположность и единство двух ее частей, одна из которых изучает числа, а другая - фигуры. Натуральные числа отличаются друг от друга своими свойствами: одни из них четны, а другие нечетны, одни являются простыми, а другие - составными, одни могут быть представлены в виде суммы двух квадратов, а другие так не представляются. Это бесконечное разнообразие свойств, столь разительно меняющихся при добавлении к числу хотя бы одной единицы, придает прелесть занятиям теорией чисел. Разумеется, столь же разнообразны по своим свойствам геометрические образы - треугольники и квадраты, окружности и параболы, астроиды и кардиоиды. Но все же каждая отдельно взятая линия, например прямая или окружность, состоит из совершенно одинаковых по своим свойствам точек.

По-разному проявляется в этих частях математики и идея бесконечности. В арифметике она воплощается как бесконечность натурального ряда чисел, а в геометрии - как бесконечность пространства и, в то же время как возможность неограниченного деления фигур на части. И все же, несмотря на эту, казалось бы, непреодолимую пропасть, связанную, быть может, с какими-то глубинными свойствами человеческого разума, на протяжении всей истории математики не прекращались попытки связать друг с другом арифметику и геометрию и постараться вывести всю математическую науку из единого основания.

В эпоху, когда математика была не столько наукой, сколько ремеслом, которым занимались египетские и вавилонские писцы, единство между арифметикой и геометрией проявлялось в наивной форме - среди различных задач рассматривали и задачи на вычисление площадей фигур и объемов тел. Первая попытка теоретического объединения арифметики и геометрии была предпринята в VI в. до н. э. в школе древнегреческого математика и философа Пифагора. Одно из дошедших до нас изречений Пифагора гласит: "Все есть число". Он не только пытался "поверить алгеброй гармонию", создав одну из первых математических теорий музыкальной гаммы, но и хотел свести к натуральным числам науку об измерении геометрических величин. Поэтому для всего миросозерцания пифагорейцев оказалось катастрофой сделанное одним из них открытие несоизмеримости стороны и диагонали квадрата (в течение длительного времени они скрывали этот факт от непосвященных).

После того как стала ясной невозможность построить геометрию на основе понятия натурального числа, древнегреческие математики, наоборот, стали выражать в геометрических терминах соотношения между любыми величинами. Хотя дискретное лучше поддавалось логическому анализу, непрерывное лучше охватывалось интуицией. На языке геометрии греческие ученые выражали алгебраические закономерности (именно с тех пор в математике укоренились термины квадрат числа, куб числа, среднее геометрическое, геометрическая прогрессия и т. д.), исследовали квадратические иррациональности, решали кубические уравнения. Саму же геометрию греческие ученые строили на идее о безграничной делимости линий, фигур и тел. Они создали абстрактные понятия о точке, не имеющей размеров, о линии, имеющей лишь длину, о геометрической поверхности. И хотя эти понятия были лишь смелым теоретическим обобщением представлений о реальных точках, линиях и поверхностях, они верно служили ученым в их исследованиях и позволяли получать с их помощью правильные формулы для площадей и объемов.

После падения античной цивилизации центр математических исследований переместился в арабоязычные страны. Ученые этих стран были знакомы не только с наследием древних греков, но и с шедшей от вавилонских писцов традицией, содержавшей общие методы решения арифметических задач. Оказали на них влияние и открытия индийских математиков, которые создали десятичную систему счисления и, в отличие от древнегреческих ученых, свободно пользовались в своих работах отрицательными числами. Все это подготовило почву для создания алгебры, которая возникла в IX в. н. э. как наука о решении уравнений. Математики той эпохи, многие из которых жили в Средней Азии, не слишком задумывались над тонкостями, связанными с несоизмеримыми отрезками, и свободно использовали числа при изучении проблем геометрии.

Через несколько столетий начались исследования по алгебре и в Западной Европе (сначала в Италии), где были получены формулы для решения уравнений третьей и четвертой степеней, начато изучение комплексных чисел и стала развиваться буквенная символика. Буквенное исчисление сначала, в соответствии с древнегреческими традициями, носило геометрическую форму, что препятствовало рассмотрению выражений, содержавших слагаемые различных степеней.

Перед математической наукой возникла необходимость построить алгебру без опоры на геометрические понятия, освободить ее от несвойственной ей геометрической терминологии. Решающий шаг в этом направлении сделал Декарт^*. На первый взгляд в его предложении не было ничего особенного - он просто предложил зафиксировать один отрезок e и назвать его единичным. Но это позволило рассматривать произведение двух отрезков a и b не как площадь прямоугольника с соответствующими сторонами, а как длину такого отрезка c, что a:e = c:b (заметим, что теория пропорций была тщательно разработана еще древнегреческими учеными). А квадратный корень из а получил истолкование как среднее геометрическое отрезков a и e. После Декарта математики могли свободно пользоваться любыми алгебраическими выражениями, не задумываясь над их геометрическим смыслом. С работ Декарта начался длившийся более двухсот лет процесс "арифметизации" математики, ее переноса с геометрического фундамента на арифметический.

^* (Декарт Рене (1596-1650) - французский математик и философ, создатель аналитической геометрии, ввел понятие переменной величины, изучал зависимости между величинами.)

В конце концов было получено свободное от геометрии определение действительных чисел. Это сделали в 70-х годах XIX в. Кантор, Вейерштрасс^*, Дедекинд и Мэре^**. Они определили действительные числа, опираясь лишь на понятие натурального числа. Поскольку со времен Декарта математики умели задавать геометрические объекты наборами действительных чисел (например, точки - их координатами), появилась возможность "арифметизировать" и геометрию. Так возникло новое единство математики, построенной на арифметическом фундаменте. Ученые этой эпохи полагали, что им удалось свести непрерывное к дискретному.

^* (Вейерштрасс Карл (1815-1897) - немецкий математик, один из создателей теории функций комплексного переменного. Построил арифметическую теорию действительных чисел и на ее основе перестроил изложение математического анализа.)

^** (Мерэ Шарль (1835-1911) - французский математик, построил арифметическую теорию действительных чисел одновременно с Вейерштрассом.)

Не случайно одним из создателей арифметического построения действительных чисел был создатель теории множеств Кантор, другим - его учитель и вдохновитель Вейерштрасс, а третьим - Дедекинд, который в своих работах очень близко подошел к идеям теории множеств. Хотя конструкции в предложенных определениях отличались друг от друга, в любой из них действительное число определялось как некоторое бесконечное множество рациональных чисел. Например, в теории Вейерштрасса действительные числа определялись как бесконечные десятичные дроби. Но чтобы задать такую дробь, надо указать десять подмножеств натурального ряда чисел: для каждой цифры - множество номеров мест, на которых она написана. А в теории Дедекинда действительное число а прямо определялось с помощью разбиения всего множества рациональных чисел на два подмножества - одно из них содержит числа, не превосходящие числа α, а второе - большие, чем α.

Одновременно с этим в работах Г. Фреге^* была сделана попытка построить на основе понятия множества саму арифметику натуральных чисел. Тем самым теория бесконечных множеств становилась общей основой как арифметики, так и геометрии, как дискретного, так и непрерывного. Получалось, что сначала надо изучить бесконечные множества, а потом выделить в их теории небольшой уголок, где скромно ютились бы конечные множества, и уже тогда получать натуральные числа. Как сказал Гильберт^**, "благодаря гигантской совместной работе Фреге, Дедекинда и Кантора бесконечное было возведено на трон и наслаждалось временем своего полного триумфа. Бесконечное в своем дерзком полете достигло головокружительной высоты успеха".

^* (Фреге Готлоб (1848-1925) - немецкий математик и логик.)

^** (Гильберт Давид (1862-1943) - крупнейший немецкий математик XX в. Автор замечательных работ в области теории инвариантов, теории алгебраических чисел, вариационного исчисления, оснований математики, функционального анализа. Ввел понятие бесконечномерного пространства.)

Однако не все ученые безоговорочно принимали новую точку зрения на математику. Вначале открытия Кантора натолкнулись на недоверие и даже прямой антагонизм многих математиков и безразличие со стороны подавляющего большинства философов. Оппозицию новым воззрениям возглавил один из виднейших алгебраистов тех лет Л. Кронэкер^*. По его убеждениям, предметом математики могло быть лишь то, что выражалось через натуральные числа за конечное число шагов. Он говорил: "Натуральные числа создал господь бог, а все остальное - дело человеческих рук". Поэтому отвергалась не только теория бесконечных множеств, считавшаяся вообще чем-то сумасбродным, по и новомодная теория действительных чисел.

^* (Кронекер Леопольд (1823-1891) - немецкий математик, работавший в области алгебры и теории чисел.)

Сдержанность, с которой многие математики приняли работы Кантора, объяснялась отчасти тем, что сама идея рассматривать бесконечность как нечто завершенное противоречила установившимся взглядам, и потому многие ученые считали исследования в области бесконечных множеств чем-то далеким от насущных задач науки. Большую роль в этом неприятии сыграл стиль работ Кантора, представлявший собой смесь математических исследований с философско-теологическими отступлениями. Трансфинитные числа настораживали тем, что с их помощью нельзя было ни вычислить какой-нибудь головоломный интеграл, ни просуммировать сложный ряд, ни решить дифференциальное уравнение. Успехи же Кантора в области конкретной математики (например, доказательство существования трансцендентных чисел) не казались слишком впечатляющими.

Но была в математике область, для которой теория множеств явилась хлебом насущным - новейшая для той поры теория функций действительного переменного. Чтобы понять, почему именно в этой области идеи Кантора оказались особенно полезными, нам придется вспомнить ход развития понятия функции.

Как развивалось понятие функции. Большинство математических понятий прошло долгий путь развития. Первоначально они возникали как обобщение каких-то наглядных представлений, повседневного опыта. Потом из этих наглядных представлений путем отбрасывания частностей и случайных черт выкристаллизовывались точные математические определения. Но часто оказывалось, что эти определения охватывают не только те объекты, изучение которых привело к формулировке данного определения, но и многие объекты, о которых раньше и не думали. Начиналось изучение этих новых объектов, переход к абстракции более высокого уровня, а потом на этой базе - расширение первоначально введенных определений. При этом в математические понятия вкладывался все более широкий смысл, они охватывали все большую совокупность объектов, получали все более разнообразные приложения.

Сложный путь прошло и понятие функции. Идея зависимости некоторых величин восходит, по-видимому, к древнегреческой науке, где она применялась в геометрии. В начале XVII в. Галилей, Кеплер и другие ученые стали развивать кинематику - науку о движении тел.^* Исходя из этих работ, Декарт ввел в математику общее понятие переменной величины. Фридрих Энгельс так оценивал значение этого события:

"Поворотным пунктом в математике была Декартова переменная величина. Благодаря этому в математику вошли движение и тем самым диалектика и благодаря этому же стало ... необходимым дифференциальное и интегральное исчисление, которое тотчас и возникает и которое было в общем и целом завершено, а не изобретено, Ньютоном и Лейбницем".

^* (Маркс К., Энгельс Ф, Соч. 2-е изд., т, 20, с. 573.)

С помощью переменных величин ученые XVII в. описывали самые разнообразные движения, в результате чего геометрический язык сменился в математике языком механики. Например, вводя в науку логарифмическую функцию, Непер^* пользовался изучением движения точек по прямой линии, а Ньютон считал, что математический анализ должен изучать зависимость от времени тех или иных величин, характеризующих движение (пути, скорости, ускорения и т. д.). Впрочем, до поры до времени сохранялся и геометрический язык. Например, рассматривали не тригонометрические функции числового аргумента, а длины некоторых отрезков в круге как функции угла. Даже само понятие функции Лейбниц ввел первоначально как связь между собой некоторых отрезков, характеризующих точки на кривой линии (абсциссы и ординаты, абсциссы и отрезка касательной между точкой касания и осью абсцисс и т. д.).

^* (Непер Джон (1550-1617) - шотландский математик, создатель теории логарифмов.)

Но уже в 1718 г. И. Бернулли^* дал определение функции, свободное от геометрических образов: "Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных". А Эйлер^** определял функцию так: "Величины, зависящие от других так, что с изменением вторых меняются и первые, принято называть их функциями". Эйлеру же удалось освободить и тригонометрию от геометрического языка - он ввел общее понятие тригонометрической функции числового переменного.

^* (Бернулли Иоганн (1667-1748) - швейцарский математик, один из создателей математического анализа, внес большой вклад в развитие понятия функции.)

^** (Эйлер Леонард (1707-1783) - математик, физик, механик и астроном. Родился в Швейцарии, большую часть жизни прожил в России. Автор замечательных работ по математическому анализу, в которых он развил общие методы интегрирования и решения дифференциальных уравнений, изучал функции комплексного переменного.)

В эпоху Эйлера считали, что функция должна быть выражена единой формулой, в противном случае ее рассматривали как "сшитую" из нескольких функций. Например, функция

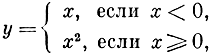
считалась состоящей из двух различных функций.

Вскоре выяснилось, что дело обстоит значительно сложнее. Решая задачу о колебании струны, Д. Бернулли^* получил ответ в виде суммы бесконечного ряда, членами которого были произведения двух тригонометрических функций, одна из которых зависела от момента времени t, а вторая - от координаты точки струны. Согласно принятому в ту эпоху мнению это означало, что отклонение струны является функцией двух переменных, имеющей, как и положено, единое выражение.

^* (Бернулли Даниил (1700-1782) - физик и математик, сын Иоганна Бернулли. Автор ряда работ в области математической физики.)

Ту же самую задачу решил Д'Аламбер, но его решение имело совсем иной вид, чем у Бернулли,- при разных значениях аргументов оно задавалось различными формулами. Перед математикой XVIII в. возникло казавшееся неразрешимым противоречие: для одной и той же зависимости получилось два результата, причем один из них для всех значений аргументов выражался одной и той же формулой, а другой - несколькими формулами. Из-за этого решение Д. Бернулли было подвергнуто сомнению: думали, что он нашел не все решения задачи, а лишь решения, выражающиеся одной формулой. Возник ожесточенный спор, в котором приняли участие все крупнейшие математики XVIII в.- Эйлер, Д'Аламбер и др.

По сути дела, спор шел о понятии функции, о связи между функциональной зависимостью и возможностью выразить эту зависимость формулой. Окончательное решение вопроса было получено в начале XIX в., когда Ж. Фурье^* показал, что сумма бесконечного ряда, состоящего из тригонометрических функций, может на различных участках выражаться различными формулами. После этого он дал новое определение функции, подчеркнув в нем, что главным является задание значений функции, а совершается ли это задание некоторой единой формулой или нет, несущественно.

^* (Фурье Жозеф (1768-1830) - французский математик. Изучал уравнения математической физики, широко используя для их решения тригонометрические ряды.)

Результаты Фурье были уточнены немецким математиком Дирихле, который показал, что графиком суммы тригонометрического ряда может быть любая, произвольно проведенная линия. Требуется лишь, чтобы число максимумов и минимумов на этой линии было конечным и линия не поднималась бесконечно высоко.

После длительного обсуждения, в котором приняли участие многие выдающиеся ученые (в том числе Н. И. Лобачевский), стало общепринятым следующее определение функции: "Переменная величина y называется функцией переменной величины x, если каждому значению величины x соответствует единственное определенное значение величины y".

В этом определении ни слова не говорилось о том, что функция должна задаваться одной и той же формулой на всем отрезке, где она определена. С современной точки зрения недочетом этого определения можно считать лишь то, что в нем идет речь о переменных величинах. Ведь с точки зрения "чистой математики" это понятие не имеет четкого определения. В начале XIX в. ученые ограничивались тем, что давали примеры переменных величин, встречающихся в физике (температура остывающего тела, путь или скорость неравномерного движения и т. д.). Они считали, что этим переменным величинам можно поставить в соответствие некую математическую переменную, изменение которой описывает ход изменения физической величины. Но при этом получалось, что одно из основных понятий математики как бы опирается на физическую идею времени.

Создание во второй половине XIX в. теории действительных чисел и построение теории множеств позволили арифметизировать и расплывчатое понятие переменной величины. Оказалось, что под переменной следует понимать букву, вместо которой можно подставлять числа, принадлежащие некоторому числовому множеству X. Разумеется, такой подход к понятию переменной был более статичным, чем принятый у ученых начала XIX в., в нем не было чувства движения, изменения. Но зато он позволил дать определение функции, свободное от лежащих вне математики понятий: "Функцией f, заданной на числовом множестве X, называется соответствие (правило), которое каждому числу x из этого множества сопоставляет число f(x)"

Столь общее определение позволило связать понятие функции с понятиями отображения, преобразования, оператора и т. д. Например, с этой точки зрения, сопоставляя каждому треугольнику его площадь, мы получаем функцию, заданную на множестве треугольников и принимающую значения в множестве положительных чисел. А сопоставляя треугольнику вписанную в него окружность, мы получаем функцию, заданную на том же множестве треугольников, но принимающую значения в множестве окружностей. Поскольку на координатной плоскости и треугольники, и окружности задаются некоторыми наборами чисел, то эти функции можно свести к некоторым числовым функциям. Вообще, числовые функции - один из важнейших видов функций, и потому в дальнейшем изложении мы ограничимся рассмотрением лишь таких функций, да к тому же заданных лишь на числовых множествах.

Под микроскопом. Уточнение математических понятий - дело обоюдоострое. При этом, конечно, устраняются многие неясности, повышается четкость математической речи, становятся более убедительными доказательства теорем. Но такие достижения влекут за собой и определенные потери. То, что выигрывает наука в строгости, она часто теряет в наглядности. Кроме того, всегда возникает вопрос, соответствуют ли понятия, получившие строгие определения, тем грубым, наглядным образам, которые они призваны моделировать в математике. Тем самым камни преткновения, убранные с поля математики, обычно не исчезают, а лишь оказываются перенесенными на границу между этой наукой и ее приложениями.

Но для математической науки точные определения являются насущной необходимостью. Изучая свойства определяемых ими понятий, ученые узнают свойства тех математических моделей, с помощью которых они пытаются описывать реальный мир. И если эти свойства оказываются непохожими на ожидаемые, то это значит лишь, что модель не вполне удачна, что при ее построении были пропущены какие-то важные стороны объектов, для описания которых она была предназначена.

Поэтому, после того как было уточнено понятие функции, математики начали его изучать со всех сторон. И тут оказалось, что под введенное определение подпадают и объекты, которые математики прошлых столетий вряд ли стали бы рассматривать. Например, уже Дирихле отметил, что функцией является и соответствие, определяемое следующим правилом:

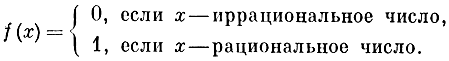
Ни одному математику XVIII в. не пришло бы в голову рассматривать такие соответствия. Они изучали лишь функции, которые описывали зависимости между физическими или геометрическими величинами. Но любое измерение конкретных величин производится с некоторой погрешностью, и потому для таких величин бессмысленно ставить вопрос, является ли их значение рациональным или иррациональным числом. Разумеется, на это можно возразить, что и значение функции

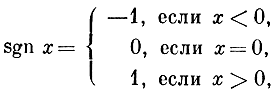
не слишком точно определено вблизи точки x = 0 - небольшая ошибка в измерении может превратить отрицательный ответ в положительный, резко изменив значение функции. По математики XVIII в. знали, что такие функции, как sgn x, являются лишь идеализированным представлением непрерывной функции, круто поднимающейся вверх на участке вблизи точки x = 0. Функция же Дирихле не годилась для самого идеализированного описания какого-либо реального процесса.

Даже добавление условия непрерывности не слишком помогало. Пользуясь обретенной свободой, математики начали строить замысловатые примеры непрерывных функций, которые противоречили всем привычным для их предшественников представлениям. Изменение, произошедшее во взглядах ученых на понятие функции в конце XIX в., Анри Пуанкаре^* охарактеризовал следующими словами: "Некогда при нахождении новых функций имелась в виду какая-нибудь практическая цель. Теперь функции изобретают специально для того, чтобы обнаружить недостаточность рассуждений наших отцов; никакого иного вывода, кроме этого, из них извлечь нельзя".

^* (Пуанкаре Анри (1854-1912) - французский математик, физик, астроном и философ, один из крупнейших математиков XX в. Ему принадлежат выдающиеся работы почти во всех областях математической науки.)

Дальнейший ход развития математики показал, что мнение Пуанкаре было односторонним - в современной физике приходится иметь дело с функциями и линиями, обладающими весьма странными свойствами. Но путь до этих приложений был еще весьма далек, и в конце XIX в. математики с увлечением последовали свойства самых чудовищных функций, которые их предшественники поместили бы разве что в кунсткамеру; не зря новую теорию функций некоторые из математиков классического направления называли "тератологии функций" (тератология - учение об уродствах).

Математики конца XIX в. как бы положили функции под микроскоп логического анализа, в то время как их предшественники смотрели невооруженным глазом и не могли открыть тонкости "микроскопического строения" этих функций. Хотя математики XVIII в. теоретически понимали, что график функции, как и всякая линия, толщины не имеет, они, думая о функциях, воспринимали их графики как начерченные на бумаге карандашом или рейсфедером, то есть имеющие некоторую толщину. А такие линии были кусочно-монотонными, то есть их графики состояли из конечного числа кусков, на которых они либо поднимались, либо опускались. Всюду, за исключением нескольких точек, к этим графикам можно было провести касательную, любые две линии в ограниченной части плоскости имели лишь конечное число общих точек и т. д.

Математики той эпохи не подозревали, что существуют функции и линии, свойства которых совсем не похожи на свойства таких "добропорядочных" функций, как многочлены, тригонометрические, показательные функции и т. д. Но в разработанном ими математическом аппарате уже содержался динамит, который впоследствии и взорвал кажущееся благополучие. Этим динамитом оказалась теория бесконечных рядов. Первоначально такие ряды возникли, чтобы облегчить вычисление значений функций. Но потом они превратились в способ получения новых функций. И тут оказалось, что при сложении столь хороших функций, как многочлены, по мере добавления новых членов начинают выступать все более мелкие дрожания будущей бесконечной суммы, и в конце концов получается функция, совсем не похожая по своим свойствам нате, которыми занимался классический анализ. Поведение таких функций напоминало математикам-классикам сумасшедший дом. Так что и здесь понятие бесконечности, идея о возможности сложить бесконечно много слагаемых, оказало революционизирующее влияние на развитие науки.

А теперь позвольте пригласить вас на прогулку по математической кунсткамере, где собраны некоторые экспонаты, которые столь же отличаются от знакомых со школьных или вузовских времен математических образов, как ихтиозавры или какие-нибудь трицератопсы от современных животных.

Джинн выходит из бутылки. Необычной является уже сама функция Дирихле, о которой говорилось выше. Ведь на самом маленьком отрезке оси абсцисс бесконечно много и рациональных чисел и иррациональных чисел. Но функция Дирихле для рациональных чисел равна единице, а для иррациональных - нулю. Поэтому когда x пробегает ось абсцисс, то значение функции все время прыгает от 0 к 1 и обратно. Построить график этой функции совершенно невозможно, потому что эта функция во всех точках разрывна.

Но и среди непрерывных функций есть функции с неожиданными свойствами. Например, может ли непрерывная функция иметь на конечном отрезке бесконечно много максимумов и минимумов? На первый взгляд это совершенно невозможно. Ведь функция должна успеть опуститься из точки максимума в точку минимума, потом опять подняться в точку максимума и т. д. Как же ей сделать все это на конечном отрезке? Тем не менее оказалось, что такие странные функции существуют, причем построить их совсем нетрудно.

Построим такую функцию на отрезке [0, 1]. Для этого разделим отрезок пополам и построим на левой половине равносторонний треугольник. Теперь разделим оставшуюся правую половину снова на две равные части и на части [¹/₂, ³/₄] построим второй равносторонний треугольник. Выполним описанную операцию бесконечно много раз. У нас получится "горная цепь", состоящая из бесконечного числа вершин, постепенно опускающаяся к точке 1 (рис. 12). Примем полученную ломаную за график функции f(x). Тогда функция будет определена в каждой точке отрезка [0, 1], за исключением крайней правой точки 1. В этой точке положим f(1) = 0.

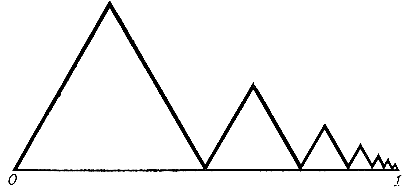
Рис. 12

Так как при приближении к точке 1 высоты вершин стремятся к нулю, полученная нами функция непрерывна во всех точках отрезка [0, 1]. А число максимумов и минимумов на этом отрезке бесконечно велико!

Математику XVIII в., чтобы построить такую странную функцию, понадобилось бы долго комбинировать различные функции, прежде чем он догадался бы, что функция

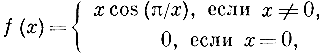
имеет бесконечно много максимумов и минимумов на отрезке [0, 1].

Но функции с бесконечным числом максимумов и минимумов были лишь началом неприятностей, ожидавших математиков. Джинн только начал выходить из бутылки.

"Мокрые точки". У функции, которую мы построили в предыдущем пункте, есть лишь одна точка, около которой бесконечно много максимумов и минимумов, а именно точка 1. Сейчас мы построим другую функцию, у которой таких точек будет куда больше.

Предположим, что на отрезок [0, 1] оси абсцисс падает сверху дождь. Для защиты от дождя поступим следующим образом. Разделим отрезок [0, 1] на три равные части и возведем над средней частью палатку в форме равностороннего треугольника. Она защитит от дождя все точки средней части (кроме концов этой части, то есть точек ¹/³ и ²/₃). Теперь каждую из оставшихся двух частей снова разделим на три равные части и защитим средние части палатками той же формы (но втрое меньшего размера).

У нас получится линия, изображенная на рис. 13. На третьем шаге процесса мы построим еще четыре палатки, потом еще восемь и т. д.

Рис. 13

Возникает вопрос: все ли точки отрезка защищены получившейся пилообразной линией или остались точки, которые дождь намочит? Некоторые из таких "мокрых" точек указать легко - ими являются концы защищаемых отрезков (то есть такие, как ¹/₃, ²/₃, ¹/₉, ²/₉, ⁷/₉, ⁸/₉ и т. д.). Все эти точки остаются без защиты при возведении соответствующей палатки, а последующие палатки их тоже не защищают. Легко видеть, что таких концов будет бесконечное, но счетное множество.

Оказывается, что кроме этого счетного множества "мокрых" точек найдется еще целый континуум таких точек. Чтобы описать их, удобно прибегнуть к троичной системе счисления, в которой все числа записываются с помощью всего лишь трех цифр: 0, 1 и 2. В этой системе счисления число "семь" записывается в виде 21, а дробь ¹/₄ - в виде 0,02020202... (чтобы убедиться в этом, надо вспомнить правило суммирования геометрической прогрессии).

Теперь мы уже можем точно сказать, какие точки останутся "мокрыми" после того, как все защитные палатки будут построены. Первая палатка защищает точки, лежащие между ¹/₃ и ²/₃. Но это те самые точки, которые в троичной системе имеют запись вида

где точками обозначена любая комбинация цифр 0, 1 и 2 (точно так же, как в десятичной системе счисления между точками ¹/₁₀ и ²/₁₀ лежат все точки, десятичная запись которых начинается с цифры 1, то есть имеет вид 0,1...). После первого шага "мокрыми" останутся точки, троичная запись которых имеет вид

или вид

Точно так же доказывается, что после возведения двух палаток на втором шаге мокрыми остаются лишь точки, троичная запись которых начинается с одной из следующих четырех комбинаций:

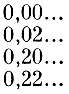
Итак, шаг за шагом защищаются от дождя точки, в троичную запись которых входят единицы. В конце концов останутся "мокрыми" лишь точки, которые можно записать в троичной системе счисления, не используя 1.

А теперь уже ясно, почему множество "мокрых" точек имеет мощность континуума. Ведь это множество можно поставить во взаимно однозначное соответствие с множеством бесконечных телеграмм. Для этого нужно лишь каждой точке вида

поставить в соответствие бесконечную телеграмму, заменив 0 на точку, а 2 - на тире. При этом разным числам будут соответствовать разные телеграммы. Мы знаем, что множество бесконечных телеграмм имеет мощность континуума. Поэтому и множество "мокрых" точек имеет ту же мощность.

Множество точек, которые мы назвали "мокрыми", впервые построил Кантор, и его называют канторовым множеством. Из построения палаток видно, что около каждой точки канторова множества есть бесконечно много максимумов и минимумов пилообразной линии.

Чертова лестница. С тем же самым канторовым множеством связана еще одна интересная функция. Она строится следующим образом. Снова разделим отрезок [0, 1] на три равные части и положим, что во всех точках средней части наша функция равна ¹/₂. Потом левую и правую трети снова разделим на три равные части и положим, что от ¹/₉ до ²/₉ функция равна ¹/₄, а от ⁷/₉ до ⁸/₉ она равна ³/₄. Теперь у нас остались четыре отрезка, на которых функция еще не определена:

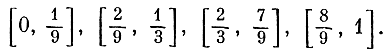
Разделим каждый из них на три равные части и на каждой из средних частей положим функцию равной соответственно

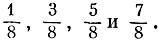
Продолжая этот процесс, мы получим функцию, которая определена во всех "сухих" точках, то есть во всех точках, не принадлежащих канторову множеству. Ее легко определить и в точках этого множества так, чтобы она стала после этого непрерывной и неубывающей. График получившейся функции приближенно изображен на рис. 14. Он имеет вид лестницы с бесконечным числом ступенек (на графике изображены не все ступени).

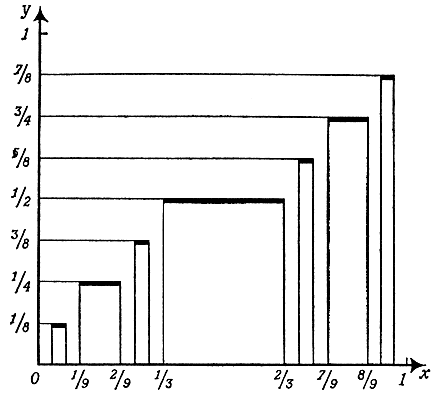
Рис. 14

Впрочем, после того как мы познакомились с линиями, имеющими бесконечно много максимумов и минимумов, лестницей с бесконечным числом ступенек вряд ли кого удивишь. Но удивительно другое. Подсчитаем общую длину всех ступенек нашей лестницы. Первая ступень имеет длину ¹/₃, две вторые - по ¹/₉, следующие четыре ступени имеют длину по ¹/₂₇ и т. д. Таким образом, сумма длин всех ступеней выражается бесконечной геометрической прогрессией

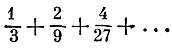
Сумма этой прогрессии равна 1:

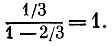
Таким образом, общая длина всех ступеней равна 1.

Но на этих ступеньках функция совсем не поднимается вверх, весь ее подъем сосредоточен в точках канторова множества. А на долю этого множества осталось очень "мало" точек: хотя его мощность и равна континууму, но длина равна нулю! (Длина всего отрезка [0, 1] равна 1, и общая длина ступенек тоже равна 1, так что на долю канторова множества остается лишь нулевая длина.) Таким образом, наша функция умудряется подняться вверх на 1, хотя растет только на множестве нулевой длины и не делает нигде скачков! Не правда ли, удивительно?

Колючая линия. На протяжении многих столетий математики имели дело лишь с линиями, почти в каждой точке которых можно было провести касательную. Если и встречались исключения, то только в нескольких точках. В этих точках линия как бы ломалась, и потому их называли точками излома. Линия, изображенная на рис. 15, а, имеет две точки излома, а линия, изображенная на рис" 15, б,- десять точек излома.

Рис. 15

Но линии, которые мы только что построили, имеют уже бесконечно много точек излома, например линия на рис. 13 ломается во всех точках канторова множества, а кроме того, в вершинах всех треугольников. Однако даже линия на рис. 13 имеет изломы на сравнительно "маленьком" множестве точек, длина которого равна нулю.

В течение долгого времени никто из математиков не верил, что может существовать непрерывная линия, целиком состоящая из зубцов, изломов и колючек. Велико было изумление, когда удалось пои строить такую линию, более того, функцию, график которой был такой колючей изгородью. Первым сделал это Больцано. Но его работа осталась неопубликованной, и впервые такой пример опубликовал Вейерштрасс. Однако пример Вейерштрасса очень трудно изложить - он основан на теории тригонометрических рядов. Пример же Больцано напоминает линии, которые мы строили раньше.

Вот этот пример с небольшими изменениями. Разделим отрезок [0, 1] на четыре равные части и над двумя средними частями построим равнобедренный прямоугольный треугольник (рис. 16, а). Получившаяся линия является графиком некоторой функции, которую обозначим через y = f₁(x).

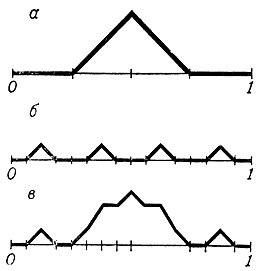
Рис. 16

Разделим теперь каждую из четырех частей еще на четыре равные части и в соответствии с этим построим еще четыре равнобедренных прямоугольных треугольника (рис. 16, б). Мы получим график второй функции y = f₂(x). Если сложить эти две функции, то график суммы y = f₁(x) + f₂(x) будет иметь вид, изображенный на рис. 16, в. Видно, что получившаяся линия имеет уже больше изломов и эти изломы гуще расположены. На следующем шаге мы снова разделим каждую часть еще на четыре части, построим 16 равнобедренных прямоугольных треугольников и прибавим соответствующую функцию y = f₃(x) к функции y = f₁(x) + f₂(x).

Продолжая этот процесс, мы будем получать все более и более изломанные линии. В пределе получится линия, у которой излом в каждой точке и ни в одной точке к ней нельзя провести касательную.

Рис. 17

Похожий пример линии, нигде не имеющей касательной, построил голландский ученый Ван-дер-Варден^*. Он взял равносторонний треугольник,разделил каждую его сторону на три равные части и на средних частях построил новые равносторонние треугольники, смотрящие наружу. У него получилась звезда. Теперь каждую из двенадцати сторон этой звезды он разделил еще на три части и снова на каждой из средних частей построил правильный треугольник. Получилась еще более колючая линия, изображенная на рис. 17. После бесконечного числа делений и построений правильных треугольников получилась линия, в каждой точке которой есть излом, колючка.

^* (Ван-дер-Варден Бартел (р. 1903) - голландский математик, работал в области алгебры, статистики, истории математики.)

Математики построили много непрерывных функций, графики которых не имели касательной ни в одной точке, и начали изучать их свойства. Эти свойства совсем не походили на свойства "добропорядочных" гладких функций, с которыми они до тех пор имели дело. Поэтому математики, воспитанные в классических традициях, с изумлением смотрели на новые функции. Более того, виднейший представитель классического математического анализа Шарль Эрмит^* так писал своему другу, голландскому математику Стилтьесу^**. "Я с ужасом отворачиваюсь от этой достойной сожаления язвы непрерывных функций, не имеющих производной ни в одной точке" (то есть, как мы их называли, всюду колючих линий).

^* (Эрмит Шарль (1822-1901) - французский математик, автор многочисленных исследований по математическому анализу, алгебре, теории чисел.)

^** (Стилтьес Томас (1856-1894) - голландский математик, автор ряда работ по математическому анализу.)

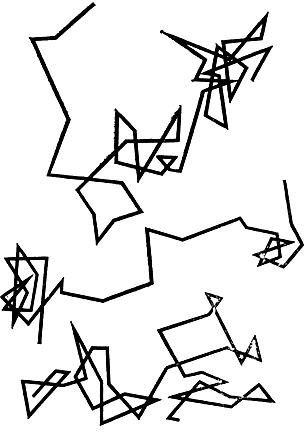
Рис. 18

В физике встречаются линии, очень напоминающие колючие линии Ван-дер-Вардена и других. Это - траектории частиц, совершающих под ударами молекул броуновское движение. Французский ученый Ж. Перрен^* сделал; зарисовки движения таких частиц. Он наблюдал их положения через каждые полминуты и соединял полученные точки прямолинейными отрезками. В результате у него получились запутанные ломаные, вроде изображенных на рис. 18. Но не следует думать, что в действительности между отдельными наблюдениями частица двигалась по прямой. Если бы Перрен наблюдал ее не через полминуты, а через полсекунды, то каждый прямолинейный отрезок пришлось бы заменить ломаной, столь же сложной, как и ломаные на рис. 18. И чем меньше были бы промежутки между наблюдениями, тем сложнее и "колючее" становилась бы ломаная. Американский математик Н. Винер^** показал, что движение броуновской частицы, настолько малой, что ее инерцией можно пренебречь, совершается по линии, нигде не имеющей касательной.

^* (Перрен Жан (1870-1942) - французский физик и физико-химик, экспериментально изучал броуновское движение.)

^** (Винер Норберт (1894-1964) - американский ученый, "отец кибернетики". Ряд его работ посвящен функциональному анализу и изучению бесконечномерных пространств.)

Замкнутая линия бесконечной длины. С линиями бесконечной длины мы встречаемся часто - бесконечную длину имеют прямая линия, парабола, гипербола и т. д. Все эти линии уходят в бесконечность, а потому и неудивительно, что их длина бесконечна. Впрочем, нетрудно построить и линию, целиком лежащую в конечной части плоскости, но имеющую бесконечную длину. Для этого надо взять окружность и намотать на нее спираль с бесконечным числом оборотов. Так как число оборотов бесконечно, а длина каждого витка больше длины окружности, то длина всей спирали бесконечна.

Но может ли существовать замкнутая линия бесконечной длины? Обычные замкнутые линии: окружность, эллипс, кардиоида - имеют конечную длину. Длина же колючей линии Ван-дер-Вардена бесконечна.

В самом деле, легко подсчитать, что после n-го шага получается линия, имеющая периметр 3*(⁴/_3ⁿ). Но при возрастании n это выражение стремится к бесконечности. Отсюда и вытекает, что длина линии Ван-дер-Вардена бесконечна.

Математический ковер. Рассказывают, что Екатерина II однажды спросила какого-то генерала, в чем разница между мортирой и гаубицей. Растерявшийся генерал ответил: "А видишь ли, государыня-матушка, мортира-то она особь статья, а гаубица - особь статья". Примерно столь же содержательный ответ можно получить, если спросить далекого от математики человека, в чем разница между линией, поверхностью и телом. Более того, он удивится, как можно спрашивать о столь очевидных вещах. Ведь всякому ясно, что линия, поверхность и тело - совсем разные вещи, и никто не назовет окружность поверхностью или сферу линией.

Но один остроумный шахматный гроссмейстер сказал, что разница между мастером и начинающим шахматистом состоит в том, что начинающему все ясно в позиции, где для мастера все полно тайны. Так же обстоит дело и с нашим вопросом. Конечно, относительно таких геометрических фигур, как квадрат или окружность, ни у кого не возникает сомнений, линии они или поверхности. Но в ходе развития науки после открытий Кантора появилось много самых причудливых геометрических фигур, относительно которых не только школьник, но и умудренный знаниями профессор математики не сразу ответит, что это такое - линия, поверхность или тело.

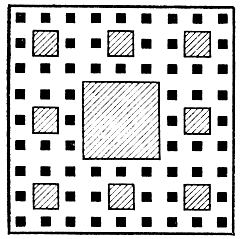
Рис. 19

Вот некоторые из этих фигур. Возьмем квадрат со стороной 1, разделим его на 9 равных квадратиков и выкинем среднюю часть (оставив ее стороны). После этого разделим каждый из оставшихся квадратов снова на 9 равных квадратиков и снова удалим центральные квадратики. Еще один такой шаг приведет к фигуре, изображенной на рис. 19, где заштрихованы все выброшенные квадратики. Ясно, что эта фигура еще является поверхностью. Но мы не остановимся и будем бесконечно много раз делить квадратики на 9 равных частей, после чего выбрасывать среднюю часть. В конце концов у нас получится геометрическая фигура, которую называют ковром Серпинского по имени придумавшего ее польского ученого.

Эта фигура похожа на ткань, сотканную сумасшедшим ткачом. Вдоль и поперек идут нити основы и утка, сплетаясь в очень симметричные и красивые узоры. Но сама получившаяся ткань весьма дырява - ни одного целого куска в ней нет, каждый самый маленький квадратик подвергался вырезанию центральной части. И совсем неясно, чем является этот ковер - линией или поверхностью? Ведь, с одной стороны, он не содержит ни одной целой части, а потому вряд ли является поверхностью, а с другой - образующие его нити сплелись в настолько сложный узор, что вряд ли кто-нибудь без колебаний назовет ковер Серпинского линией. Во всяком случае, нарисовать эту "линию" было бы невозможно.

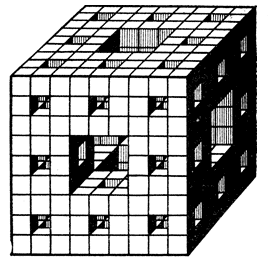
Рис. 20

А ковер Серпинского - не самая сложная из геометрических фигур. Вместо квадрата мы разделим кубик на 27 равных кубиков и выбросим центральный кубик вместе о шестью прилегающими к нему кубиками. После этого разделим каждый оставшийся кубик еще на 27 частей и продолжим операцию выбрасывания (на рис. 20 изображено тело, остающееся после двух выбрасываний). Проделаем эту операцию бесконечно много раз. Чем является оставшаяся после всех выбрасываний геометрическая фигура - линией, поверхностью или телом?

Евклид отказывает в помощи. Когда перед математиками прежних времен вставал сложный геометрический вопрос, они в первую очередь отправлялись смотреть, что написано об этом у Евклида. Ведь на протяжении почти двух тысячелетий Евклид был эталоном математической строгости и энциклопедией геометрической мудрости. Не зря даже философы, стремясь обезопасить себя от упреков в нестрогости рассуждений, прибегали к языку Евклида и формулировали свои утверждения как аксиомы, леммы и теоремы.

Но как раз по интересующему нас вопросу у Евклида написано нечто совсем невнятное. Первые строки книги Евклида "Начала" гласят следующее:

1. Точка есть то, что не имеет частей.
2. Линия же - длина без ширины.
3. Оконечность же линии - точка.
4. Поверхность есть то, что имеет только длину и ширину.
5. Оконечность же поверхности - линия.
6. Граница есть то, что является оконечностью чего-либо.
7. Фигура есть то,- что содержится внутри какой-нибудь или каких-нибудь границ.

Нет, как хотите, а это что угодно, но не строгие математические определения. Человек, не знающий, что такое точка, линия, поверхность, вряд ли почерпнет полезные для себя сведения из этих "определений", напоминающих ответ растерявшегося генерала ("Линия - это особь статья, а поверхность - особь статья"). И уж во всяком случае из этих определений не удастся узнать, что такое ковер Серпинского - линия или поверхность,; есть ли у него только длина без ширины или и длина, и ширина.

Но во времена Евклида таких сложных фигур, как ковер Серпинского, не знали, а для простых фигур определения были не слишком нужны: всякий и так мог увидеть, где на чертеже линия, а где поверхность. Впрочем, и сам Евклидг по-видимому, чувствовал, что с определениями основных понятий у него не все ладно. Во всяком случае, приведя эти определения в начале книги, он потом начисто о них забыл и ни разу на протяжении всего труда ими не воспользовался.

Нужны ли строгие определения? На протяжении двух тысячелетий авторитет Евклида стоял совершенно незыблемо. Усомниться в каком-нибудь его положении означало окончательно и бесповоротно подорвать свою математическую репутацию. Один из величайших математиков XIX в. Карл Фридрих Гаусс, еще до Лобачевского пришедший к идеям неевклидовой геометрии, не решился опубликовать свои исследования, опасаясь, как он писал одному другу, крика беотийцев^*. И только научный подвиг великого русского геометра Николая Ивановича Лобачевского, который опубликовал свои открытия, невзирая на насмешки не понимавших его ученых, сделал неевклидову геометрию всеобщим достоянием.

^* (Беотийцы - греческое племя, которое считалось весьма экономно наделенным умственными способностями.)

После появления трудов Н. И. Лобачевского стало ясно, что существуют две геометрии, одинаково безупречные логически, но приводящие к совершенно различным теоремам. Но если это так, то всякие ссылки на "геометрическую очевидность" полностью потеряли цену. Каждое геометрическое утверждение надо было основывать на строгих определениях, безупречных логических утверждениях. И уж во всяком случае основным геометрическим понятиям - линии, фигуре, телу - надо было дать точные определения, ничем не напоминающие определения типа "это - особь статья, а то - особь статья".

Стремление к строгим определениям характеризовало не только геометрию, но и математический анализ XIX в.

С помощью дифференциального и интегрального исчислений, созданных трудами Ньютона, Лейбница, Эйлера, Лагранжа^* и других великих математиков XVII и XVIII вв., удалось решить самые разнообразные задачи - от расчета траектории артиллерийского снаряда до предсказания движений планет и комет. Но основные понятия, с помощью которых достигались эти замечательные результаты, были определены крайне нестрого. Основа тогдашнего математического анализа - понятие бесконечно малой величины казалось чем-то стоящим на грани бытия и небытия, чем-то вроде нуля, но не совсем нуля. И математики XVIII в. были вынуждены ободрять своих сомневающихся учеников словами: "Работайте, и вера к вам придет".

^* (Лагранж Жозеф (1736-1813) - французский математик и механик, один из создателей вариационного исчисления, автор ряда работ в области математического анализа и его приложений.)

Но ведь математика не религия, строить ее на вере нельзя. А самое главное - методы, дававшие столь замечательные результаты в руках великих мастеров, стали приводить к ошибкам и парадоксам, когда ими стали пользоваться менее талантливые ученики. Мастеров оберегала от ошибок их абсолютная математическая интуиция, то подсознательное чувство, которое часто приводит к правильному ответу скорее, чем длинные логические рассуждения. Ученики же такой интуицией не обладали, и конец XVIII в. ознаменовался неслыханным скандалом в математике - наплывом формул, стоивших меньше, чем бумага, на которой они были напечатаны, и сомнительных теорем, область приложимости которых была совершенно неясна.

И, подобно детям, ломающим красивую игрушку, чтобы посмотреть, как она устроена, математики XIX в. подвергли жестокой критике все применявшиеся до того понятия, стали перестраивать математику на базе строгих определений. Ссылки на наглядность отвергались, вместо нее требовали строжайшей логики. Но требованиям логики не удовлетворяли самые простые фразы из курса математического анализа, например такие, как:

"Рассмотрим область G₁ ограниченную замкнутой линией Г".

Что такое замкнутая линия? Почему она является границей области? На сколько частей замкнутая линия разбивает плоскость и какую из этих частей рассматривают?

На все эти вопросы математики XVIII в. не давали ответа. Они просто рисовали овал и думали, то этим все сказано. А в XIX в. рисункам уже не верили. Для аналитиков вопрос "что такое линия?" тоже стал одним из самых жгучих.

Однако прошло много времени, прежде чем удалось дать на него исчерпывающий ответ.

Линия - след движущейся точки. Для того чтобы дать строгое определение линии, надо было исходить из тех наглядных образов, которые привели к созданию этого математического понятия: длинных и тонких нитей, лучей света, длинных и узких дорог. Во всех этих случаях длина настолько больше ширины, что шириной можно пренебречь. В результате математической идеализации мы и приходим к понятию линии, не имеющей ширины.

Первым попытался дать строгое определение того, что такое линия, Камилл Жордан^*. Линией он называл траекторию движущейся точки. При этом точка должна была двигаться непрерывно, не делая скачков.

^* (Жордан Камилл (1838-1922) - французский математик, один из создателей теории групп.)

Более точно определение Жордана звучало следующим образом. Для того чтобы задать положение движущейся точки, надо задать ее координаты в каждый момент движения. Так как движение продолжается какой-то конечный промежуток времени, то, не теряя общности, можно считать, что этим промежутком является [0, 1]. Иными словами, точка начинает двигаться в некоторый момент времени, принимаемый за начало отсчета, и кончает движение по истечении некоторой единицы времени (одной секунды, минуты, года и т. д.). В каждый момент времени t в течение этого промежутка задаются координаты движущейся точки. Таким образом, координаты точки зависят от момента времени t, являются его функциями. Обозначим эти функции (для случая, когда движение точки происходит в одной плоскости) через f(t) и g(t): x = f(t), y = g(t). Условие, что точка движется непрерывно, означает, что функции f(t) и g(t) непрерывны в каждой точке отрезка [0, 1]. Грубо говоря, при малом изменении t функции f(t) и g(t) должны мало изменяться.

Определение Жордана оказалось довольно удачным. Дуги всех линий, с которыми имели дело математики того времени, оказались кривыми в смысле Жордана, или, как говорят, жордановыми кривыми. Даже линии, составленные из дуг различных кривых, относятся к этому классу.

Теорема очевидна, доказательство - нет. Жордану удалось, используя введенное им понятие кривой, уточнить смысл той самой фразы из учебников математического анализа, о которой мы уже говорили: "Пусть замкнутая линия Г ограничивает область G". Замкнутая жорданова кривая - это кривая, которая при t = 1 попадает в ту же точку, где она была при t = 0. Если при этом различным моментам времени t₁ и t₂, лежащим между 0 и 1, соответствуют разные точки кривой, то эта кривая не пересекает саму себя.

Жордан доказал следующую теорему.

Замкнутая жорданова кривая Г, не имеющая точек самопересечения, разбивает всю плоскость на две части. Две точки, принадлежащие одной и той же части, можно соединить ломаной, не пересекающей кривую Г, а точки из разных частей нельзя соединить такой ломаной, любая соединяющая их ломаная пересекает кривую Г (рис. 21).

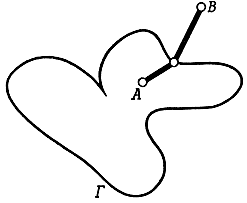
Рис. 21

Эта теорема кажется совершенно очевидной. Однако ее доказательство потребовало очень тонких рассуждений. Даже в случае, когда линия Г является замкнутым многоугольником, доказательство остается очень сложным.

Две части, на которые замкнутая жорданова линия разбивает плоскость, называют внутренней и внешней областями, ограниченными этой линией. Таким образом, понятие области, ограниченной замкнутой линией, приобрело точный смысл.

Кривая проходит через все точки квадрата. Когда Жордан дал свое определение кривой, то сначала казалось, что цель достигнута, получено строгое определение понятия линии, не опирающееся на наглядность. Но вскоре оказалось, что это не так. Определение Жордана охватывало не только привычные для математиков линии, но и фигуры, которые никто бы линиями не назвал. Уж со всюду колючими линиями математики как-нибудь примирились бы. Но назвать линией квадрат, на это ни у кого не хватило бы духу. А оказалось, что и квадрат, и треугольник (не периметр треугольника, а сам треугольник со всеми его внутренними точками), и круг являются линиями в смысле Жордана. Доказал это итальянский математик Пеано^*.

^* (Пеано Джузеппе (1858-1932) - итальянский математик, занимался теорией дифференциальных уравнений и формальнологическим обоснованием математики.)

Мы уже рассказывали, что Кантор установил взаимно однозначное соответствие между точками отрезка и квадрата, то есть показал, что отрезок содержит ровно столько же точек, что и квадрат. Построенное им соответствие не было непрерывным. Когда точка двигалась по отрезку, соответствующая ей точка на квадрате не ползла подобно жуку, а прыгала как блоха. В самом деле, возьмем на отрезке точки

Эти точки довольно близки друг к другу. Но соответствующие им точки на квадрате далеки друг от друга. Ведь первой из них соответствует точка (0,50000... , 0,0000...), лежащая на нижней стороне квадрата, а второй - точка (0,4999000... , 0,9999000...), лежащая у самой верхней стороны квадрата. И если мы будем увеличивать число девяток у второй точки, приближая ее к первой, то соответствующие точки квадрата и не подумают приближаться друг к другу.

Таким образом, канторово отображение отрезка на квадрат хотя и было взаимно однозначным, но не было непрерывным. Оно не давало, таким образом, жордановой кривой. Пеано удалось построить другое отображение множества точек отрезка на множество точек квадрата, при котором близким точкам на отрезке соответствовали близкие точки квадрата. Иными словами, Пеано удалось построить кривую линию (в смысле Жордана), которая прошла через все точки квадрата!

Разумеется, мы не можем нарисовать кривую Пеано, разве что, подражая художнику-абстракционисту, нарисуем черный квадрат. Но ведь на этом квадрате все равно нельзя будет понять, где начинается кривая, где она кончается, как она обходит квадрат. Поэтому последуем примеру не художника-абстракциониста, а физика Перрена и будем приближенно изображать путь точки в виде ломаной. Чем меньше будут промежутки времени между отдельными "наблюдениями", тем точнее получившаяся ломаная изобразит кривую Пеано.

Сначала будем отмечать положение движущейся точки через каждые ¹/₄ с. Иными словами, отметим ее положение в начале движения, через ¹/₄ с после начала движения, через ¹/₂ с после начала движения, через ³/₄ с и в конце движения. Мы получим 5 точек. Соединив их, получаем линию ABCDE, изображенную на рис. 22, а.

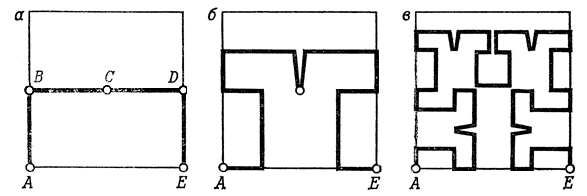
Рис. 22

Разумеется, эта линия не проходит через все точки квадрата. Но мы уменьшим промежутки времени между отдельными наблюдениями и будем отмечать положение точки каждые ¹/₁₆ с. Линия станет более извилистой, увеличится число изломов, и она примет вид, изображенный на рис. 22, б. Если еще чаще отмечать положение движущейся точки, то получим линию, изображенную на рис. 22, в. Мы видим, что линия все плотнее и плотнее заполняет квадрат, все ближе и ближе подходит к каждой его точке. В пределе, если все время наблюдать за движущейся точкой, мы получим линию, проходящую через все без исключения точки квадрата.

Надо отметить, что, выиграв по сравнению с Кантором в том, что его линия оказалась непрерывной, Пеано потерял в другом. Его линия уже не задавала взаимно однозначного отображения отрезка на квадрат. Через некоторые точки квадрата она проходила по нескольку раз. Позже было доказано, что невозможно сохранить одновременно и непрерывность, и взаимную однозначность соответствия: не существует жордановой кривой, проходящей через все точки квадрата в точности по одному разу!

Все лежало в развалинах. Трудно передать словами впечатление, произведенное на математический мир результатом Пеано. Казалось, что все рухнуло, что самые основные математические определения потеряли всякий смысл, не было видно различия между линией и поверхностью, поверхностью и телом (результат о невозможности взаимно однозначного и непрерывного соответствия между отрезком и квадратом еще не был известен). Пуанкаре с горечью воскликнул: "Как могла интуиция до такой степени обмануть нас!"

Стало ясно, что жорданово определение кривой не безупречно. С одной стороны, оно слишком широко: под него подходит и кривая Пеано. А с другой стороны, оно слишком узко - даже окружность с намотанной на нее спиралью уже не является жордановой кривой.

Итак, снова встал вопрос: что же такое линия и чем она отличается от поверхности? Ответ на него был связан с общими исследованиями Кантора о геометрических фигурах.

Как делают статуи. Создав теорию множеств, Кантор перешел к вопросу о том, что такое геометрическая фигура? Самый общий ответ на этот вопрос гласил: геометрическая фигура - это любое множество точек пространства. Если это множество лежит на плоскости, то получается плоская геометрическая фигура. Но такой ответ был бы слишком общим - у "фигур" в этом смысле нет почти никаких достаточно интересных свойств.

Поэтому надо было в первую очередь ограничить совокупности изучаемых множеств, выделить из них те, которые ближе всего по своим свойствам к обычным геометрическим фигурам.

Чтобы выделить такой класс фигур, выясним, что общего имеют друг с другом обычные фигуры, такие, как квадрат, круг, отрезок прямой, астроида и т. д. Оказывается, все эти фигуры можно получить единообразным процессом.

Про многих знаменитых скульпторов рассказывают, что на вопрос, как удается делать столь замечательные статуи, следовал ответ: "Я беру глыбу мрамора и отсекаю от нее все лишнее". В разных книгах это можно прочитать о Микеланджело, о Торвальдсене, о Родене.

Тем же самым способом можно получить любую ограниченную плоскую геометрическую фигуру: надо взять какой-нибудь квадрат, в котором она лежит, а потом отсечь все лишнее. Однако отсекать надо не сразу, а постепенно, на каждом шагу отбрасывая кусочек, имеющий форму круга. При этом сам круг выбрасывается, а его граница - окружность - остается в фигуре.

Рис. 23

На первый взгляд кажется, что так можно получить лишь фигуры такого вида, как на рис. 23. Но все дело в том, что отбрасывают не один и не два круга, а бесконечное, точнее говоря, счетное множество кругов. Таким путем можно получить любую фигуру. Чтобы убедиться в этом, достаточно принять во внимание, что множество кругов, у которых рациональны и радиус и обе координаты центра, счетное (это легко доказывается описанными во второй главе методами). А теперь, чтобы получить любую фигуру, достаточно взять содержащий ее квадрат ("глыбу мрамора") и отбросить все круги указанного выше вида, которые не содержат ни одной точки нужной нам фигуры. Если же выбрасывать круги не из квадрата, а из всей плоскости, то описанным приемом можно получить и неограниченные фигуры.

С помощью описанного выше метода можно получить круги и квадраты, эллипсы и астроиды, любые правильные многоугольники и звезды. Но получить таким путем квадрат с выброшенной вершиной не удастся - при попытке вырезать эту вершину придется удалить и какую-то ее окрестность. В математике фигуры, получаемые из плоскости вырезанием счетного множества кругов (напомним, что при этом граница выбрасываемого круга остается нетронутой), называют замкнутыми.

Континуумы. Оказывается, что кроме обычных геометрических фигур с помощью выбрасывания счетного множества кругов (квадратов и т. д.) можно получать и другие множества, не слишком похожие на обычные фигуры, но все же обладающие многими интересными свойствами. Например, ковер Серпинского, о котором мы уже говорили, получается именно таким путем: из квадрата со стороной 1 выбрасывают один за другим маленькие квадратики, причем их стороны остаются.

Рис. 24

Однако путем выбрасывания можно получить и "фигуры", не состоящие из одного куска. Например, если удалять "кресты"^*, как на рис. 24, то получится в конце концов множество, не содержащее ни одного целого куска (как говорят, вполне несвязное). Поэтому мы введем ограничение, что после каждого выбрасывания должно оставаться множество, состоящее из одного куска. Тогда и после всех выбрасываний останется множество из одного куска (то есть, как говорят математики, связное). Кроме того, получающееся множество ограничено, то есть целиком лежит в некотором квадрате.

^* (При этом вместе с каждым крестом удаляются его концевые промежутки, например промежутки AB, CD, EF, GH.)

Итак, рассматриваемые множества удовлетворяют следующим условиям:

1. множество F получается из квадрата выбрасыванием счетного множества кругов с оставлением их границ, то есть замкнуто;
2. множество F состоит из одного куска, то есть связно.

Эти множества Кантор и назвал континуумами (напомним, что латинское слово continuum означает непрерывный). Континуумы и оказались наиболее общими множествами, свойства которых очень близки к свойствам обычных геометрических фигур.

Канторовы линии. Теперь мы уже готовы ответить на вопрос, что же такое плоская линия. Так как плоские линии должны быть геометрическими фигурами, то ясно, что искать их надо среди континуумов. Но континуумами являются и круг, и квадрат, а эти фигуры никак не назовешь линиями. Поэтому надо добавить еще какое-то условие, которое отмело бы такие фигуры.

Заметим, что и круг, и квадрат содержат "сплошные" куски плоскости. А линии сплошных кусков плоскости не содержат; какой бы маленький квадратик мы ни взяли, всегда на нем найдутся точки, не принадлежащие линии (рис. 25). Вот это и является нужным нам дополнительным условием: плоской линией в смысле Кантора называют лежащий на плоскости континуум, не заполняющий ни одного сплошного куска плоскости (то есть такой, что в каждом квадрате есть точки, не принадлежащие этой линии).

Рис. 25

Например, отрезок, контур треугольника, окружность, четырехлепестковая роза - все это линии. Линией является и ковер Серпинского. Так как при его построении мы продырявили все квадраты, получавшиеся при делении, то ни одного целого куска плоскости он не содержит. Канторовой линией является и окружность вместе с намотанной на нее спиралью, и пилообразная линия на рис. 26 вместе с отрезком [0, 1] оси ординат. Вообще все фигуры, являющиеся линиями в наглядном, наивном понимании, являются линиями и в смысле Кантора. А фигуры, содержащие хоть один целый кусок плоскости, не относятся к числу канторовых линий.

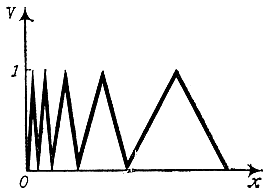
Рис. 26

Но и среди канторовых линий есть такие, что их свойства совершенно непохожи на свойства обычных линий. Сейчас мы расскажем о некоторых таких линиях.

Всегда ли площадь линии равна нулю? Конечно, после того как читатель познакомился с линиями, проходящими через все точки квадрата, он может ожидать чего угодно. Но все же, может ли линия иметь площадь? Ведь еще Евклид говорил, что линия - это длина без ширины. А там, где нет ширины, нет, казалось бы, и площади. Да и в определении канторовой линии сказано, что она не содержит ни одного целого куска плоскости. Откуда же в этом случае взяться площади? Но мы уже много раз видели, что применение бесконечных процессов приводит к совсем неожиданным результатам.

Прежде чем исследовать вопрос, надо договориться о точном смысле употребляемых слов. Что значат слова "линия имеет нулевую площадь" или "линия имеет ненулевую площадь"? Возьмем самую обычную линию - прямолинейный отрезок. Так как его ширина равна нулю, то отрезок можно поместить внутрь прямоугольника сколь угодно малой площади, нужно лишь выбрать ширину этого прямоугольника достаточно малой. Точно так же и окружность можно поместить внутрь многоугольника со сколь угодно малой площадью. Для этого достаточно вписать в нее правильный многоугольник с очень большим числом сторон и описать аналогичный многоугольник. Область, заключенная между этими двумя многоугольниками, будет иметь малую площадь (тем меньшую, чем больше сторон у наших многоугольников), а окружность целиком лежит в этой области (рис. 27).

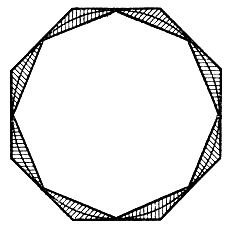
Рис. 27

Теперь уже ясно, что означают слова линия имеет нулевую площадь. Они значат, что, какое бы маленькое положительное число ε мы ни взяли, найдется многоугольная область, содержащая линию и такая, что площадь области меньше, чем ε. А если хоть для одного положительного ε такой области не удастся найти, тогда площадь линии не равна нулю.

Применим теперь это определение не к таким простым линиям, как отрезок или окружность, а к более сложным, например к ковру Серпинского. Простой подсчет показывает, что после n выбрасываний остается фигура, площадь которой равна (⁸/₉)ⁿ. Но ⁸/₉ - правильная дробь, а при возведении такой дроби в степень с увеличением показателя результат уменьшается и стремится к нулю. Это означает, что для любого ε>0 после достаточно большого числа шагов получится многоугольная область, площадь которой меньше, чем ε. А эта область целиком накрывает ковер Серпинского. Выходит, площадь ковра Серпинского равна нулю.

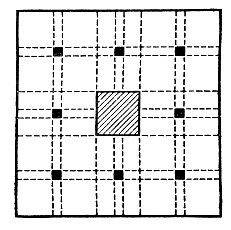
Рис. 28

Казалось бы, полный триумф определения Евклида. Даже у такой сложной линии, как ковер Серпинского, площадь равна нулю. Но праздновать победу преждевременно. Ведь никто не заставлял нас выбрасывать такие большие куски. На рис. 28 изображен более экономный способ выбрасывания квадратиков. Подбирая должным образом их размеры, можно добиться того, чтобы общая площадь выброшенных фигур не превышала ¹/₂. Но тогда на каждом шагу описанного процесса будет оставаться многоугольная область, площадь которой никак не меньше, чем ¹/₂. Отсюда легко следует, что остаток, получающийся после всех выбрасываний, не удастся покрыть многоугольной областью, если ее площадь окажется меньше, чем ¹/₂. Значит, о нем нельзя сказать, что его площадь равна нулю. А ведь этот остаток, как и ковер Серпинского, является кривой (в смысле Кантора) - при его построении мы дырявили каждый прямоугольник и ни одного целого прямоугольника не оставили.

Выходит, таким образом, что кривая в смысле Кантора может иметь ненулевую площадь!

Области без площади. Все же разобранный пример еще не слишком убедителен: полученная линия сплошь состоит из точек самопересечения и не ограничивает никакой области. Поэтому возникает вопрос: а может ли "хорошая" кривая, не имеющая точек самопересечения, то есть замкнутая жорданова кривая без самопересечений, иметь ненулевую площадь? Оказывается, может!

Чтобы построить такую кривую, изменим немного проводившееся построение. Сначала построим множество, в котором не только что целого куска плоскости, а и целого куска линии не найдешь, но площадь которого не равна нулю. Для этого надо выбрасывать не только центральные квадратики, а целые кресты, как это показано на рис. 29. При этом размеры удаляемых фигур подберем так, чтобы общая площадь их оказалась меньше половины площади всего квадрата. Тогда на долю остатка придется по крайней мере половина всей площади квадрата. Но при построении остатка мы выбрасывали целые кресты, безжалостно кромсая квадрат. Никакие две точки этого остатка нельзя соединить линией, даже линией в смысле Кантора; всякая связь между его точками отсутствует. Как говорят математики, остаток является вполне несвязным множеством. А площадь этого множества, не содержащего ни целого куска плоскости, ни дуги кривой, отлична от нуля; никакой многоугольной областью, площадь которой меньше ¹/₂, это множество не накроешь.

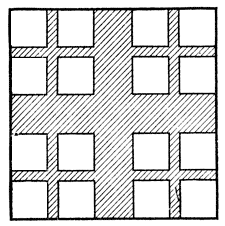
Рис. 29

Теперь уже легко построить пример несамопересекающейся замкнутой кривой, имеющей ненулевую площадь. Для этого нужно соединить полученные точки точно так же, как мы проводили кривую через все точки квадрата. Из-за того, что на каждом шагу мы выбрасывали целые кресты, получающаяся линия не имеет самопересечений (этим она и отличается от кривой Пеано). Но так как она проходит через все точки множества, площадь которого по крайней мере равна ¹/₂, то и площадь полученной линии по крайней мере равна ¹/₂.

Теперь уже ничего не стоит построить область, не имеющую площади. Для этого надо соединить точки А и В полученной кривой какой угодно линией, например полуокружностью. Тогда полученная линия Г ограничивает какую-то область G. Чему же равна ее площадь? Ответ получится разный в зависимости от того, присоединим мы к этой области ее границу или нет - ведь сама граница имеет площадь, по крайней мере равную ¹/₂. Ясно, что обычной площади наша область не имеет. Такие области, не имеющие обычной площади, в математике называют неквадрируемыми.

А все-таки их можно измерить. Над тем, что такое площадь фигуры, математики задумались еще до открытия неквадрируемых областей. До этого на протяжении многих тысячелетий ученые пользовались понятиями длины, площади, объема, не подвергая их строгому критическому анализу. Рассказывают, что когда один французский генерал принес в Парижскую академию наук свое "решение" проблемы квадратуры круга, его спросили, а что именно он понимает под площадью круга. "Площади не определяют, их вычисляют!" - воскликнул бравый генерал. И такая точка зрения была распространена тогда даже среди математиков. Они считали, что площадь - это число, сопоставленное геометрической фигуре и обладающее очевидными свойствами (площадь целого равна сумме площадей частей, конгруэнтные фигуры имеют равные площади и т. д.). Ни на одну минуту они не сомневались в том, что любая плоская геометрическая фигура имеет площадь (быть может, равную нулю или бесконечности).

Но характерной чертой математики является то, что наряду с созданием новых методов решения практических задач она изучает и оттачивает применяемый ею инструментарий, для каждого возникающего понятия ищет наиболее широкую и естественную область его применимости, для каждой доказанной теоремы - наиболее общие условия, при которых она справедлива. И это не пустые занятия математических снобов, а необходимость. Только установив понятия и теоремы в наибольшей общности, освободив их от ненужных ограничений, связанных с той конкретной задачей, из которой они возникли, можно увидеть связи между далекими друг от друга областями науки, научиться применять созданные методы в ситуациях, не имеющих на первый взгляд ничего общего с первоначальными источниками этих методов.

Поэтому столь очевидные, казалось бы, понятия, как длина, площадь, объем (позднее все эти понятия стали называть одним словом - мера), были подвергнуты тщательнейшему анализу. Одна из первых работ по уточнению понятия меры принадлежала Жордану. В течение многих десятилетий он читал в Париже курс математического анализа, построенный на самых точных определениях, безупречных доказательствах и строжайшей логике. И, конечно, он не мог пользоваться в этом курсе расплывчатым понятием площади. Придуманное им определение площади можно сформулировать так: площадь фигуры - это число, которое лежит между множеством площадей многоугольников, содержащихся в этой фигуре, и множеством площадей многоугольников, содержащих ту же фигуру. Оказалось, что площадь по Жордану имеют те и только те плоские фигуры, граница которых имеет нулевую площадь. К сожалению, слишком много фигур не поддавалось измерению по Жордану; в частности, нельзя было измерить описанные выше неквадрируемые области.

За решение возникших проблем взялись молодые ученые, вдохновленные лекциями Жордана. Одно из первых определений, применимых к весьма широкому классу фигур, предложил в конце XIX в. Эмиль Борель^*. Он заметил, что все возникавшие в науке фигуры на прямой, плоскости и в пространстве могли быть получены из простейших фигур - отрезков, квадратов и кубов с помощью двух основных операций: образования дополнения к множеству и объединения счетной совокупности множеств (в частности, как мы видели выше, таким путем получаются все замкнутые множества). Чередуя эти операции и продолжая такой процесс трансфинитным образом, можно получать на каждом шагу все более сложные множества, названные в честь Бореля борелевскими, или, иначе, B-множествами (отметим, что, применяя идею Зенона, можно получить каждое такое множество за конечный промежуток времени, удваивая на каждом шагу скорость применяемых операций).

^* (Борель Эмиль (1871-1956) - французский математик, автор работ по теории функций действительного переменного n многим областям математического анализа.)

Оказалось, что любому борелевскому множеству можно приписать меру исходя из следующих двух принципов:

• если множество A представило в виде объединения счетной совокупности подмножеств, имеющих меру, причем никакие два из них не имеют общих точек, то мера всего множества равна сумме ряда, составленного из мер подмножеств;
• мера дополнения к подмножеству, имеющему меру, получается путем вычитания меры этого подмножества из меры целого.

Из принципов Бореля вытекало, в частности, что любое счетное множество имеет нулевую меру - ведь оно является объединением счетной совокупности точек, а мера каждой из этих точек равна нулю.

К сожалению, позднее выяснилось, что предложенный Борелем процесс измерения множеств обладал существенным недостатком. Дело в том, что одно и то же множество может быть разными способами составлено из простейших, а потому предстояло доказать, что все эти способы дадут одно и то же значение для меры данного множества. Такого доказательства Борель не смог получить.

Иначе подошел к проблеме измерения множеств начинавший в те годы свою научную деятельность Анри Лебег^*. Уже первые работы Лебега разгневали математиков классического направления. Само название одной из них "О нелинейчатых развертывающихся поверхностях" казалось им столь же противоестественным, как, например, название "О газообразном льде" для физика или "О рыбообразных слонах" для биолога. Самый слабый студент знал, что любая поверхность, которую можно развернуть на плоскость (цилиндр, конус и т. д.), соткана из прямых линий, то есть может быть получена движением прямолинейной образующей. Но все дело было в том, что молодой автор по-иному понимал развертывающиеся поверхности, чем геометры-классики. Он считал такими не только поверхности, получаемые аккуратным изгибанием листа бумаги, но и поверхности, которые получатся, если этот лист бумаги скомкать (поясняя свою работу одному из друзей, Лебег сказал: "Представь себе скомканный носовой платок"). Он доказал, что кусок плоскости можно так "скомкать", чтобы после этого на нем не оказалось ни одного прямолинейного отрезка. Разумеется, получившаяся поверхность вся состояла из складок и изломов. Поэтому ее и пропустили геометры, классифицировавшие развертывающиеся поверхности: они занимались лишь гладким случаем.

^* (Лебег Анри (1875-1941) - французский математик. Ввел обобщение понятия интеграла, широко используемое в современной математике.)

От изучения произвольных развертывающихся поверхностей Лебег перешел к общему вопросу, как определить площадь поверхности, если эта поверхность не является гладкой, если к ней нигде нельзя провести касательную плоскость. Для скомканной развертывающейся поверхности задача решается просто: надо расправить ее и подсчитать площадь получившегося куска плоскости. Но этот ответ нельзя было получить по формулам, которые давала классическая математика: они годились лишь для гладких поверхностей.

Не удалась бы и попытка измерять площади поверхностей, вписывая в них многогранники и переходя к пределу при уменьшении размеров всех граней. Немецкий математик Г. Шварц^* показал, что таким путем нельзя найти площадь самого обычного цилиндра - вписанный в него многогранник может оказаться настолько складчатым, что площадь его поверхности куда больше площади цилиндра. Лебегу удалось придумать определение площади поверхности, которое не требовало проведения касательных плоскостей, но в то же время обходило все трудности, связанные с "гармошкой Шварца". Решая эту частную задачу, Лебег пришел к общим идеям о том, что такое мера множества, как измерять длины, площади и объемы самых причудливых фигур.

^* (Шварц Герман (1843-1921) - немецкий математик, автор работ в области математического анализа.)

Взяв от Бореля идею суммирования рядов, он видоизменил определение меры, предложенное Жорданом, разрешив использовать кроме многоугольников и фигуры, получаемые из них с помощью объединения счетных совокупностей. Именно, назовем фигуру ε-покрываемой по Лебегу, если существует счетная система многоугольников, объединение которых покрывает эту фигуру, причем сумма ряда, составленного из их площадей, меньше, чем ε. Далее, назовем множество X измеримым по Лебегу, если для любого ε>0 его можно представить в виде многоугольника Δε, к которому присоединено одно ε-покрываемое множество и от которого отброшено другое ε-покрываемое множество. Если меру многоугольника A обозначить через |A|, то ясно, что мера множества X должна быть заключена между числами |A_ε|-ε и |A_ε|+ε. Оказалось, что для измеримых по Лебегу множеств всегда существует одно и только одно число, обладающее этим свойством, какое бы ε>0 мы ни выбрали и какой приближающий многоугольник A_ε ни взяли. Это-то число и называют мерой Лебега множества X.

После создания понятия меры Лебега оказалось, что для нее нет никаких осложнений, причем по Лебегу можно измерить все встретившиеся до того в науке множества. Позднее были построены примеры неизмеримых множеств, но они используют так называемую аксиому выбора, о которой будет идти речь ниже. Построенные с ее помощью примеры не являются конструктивными. Поэтому можно сказать, что Лебег решил проблему измерения всех множеств, которые могут встретиться в практической работе математиков.

С помощью введенного им понятия меры Лебег сумел найти интегралы всех разрывных функций, которые можно было построить известными в то время методами (интеграл Лебега).

Триумф идей Лебега привел к тому, что даже один из вождей математиков-классиков Гастон Дарбу^* изменил свое мнение и, выступая в 1908 г. на Математическом конгрессе в Риме, говорил о пламенном и пытливом духе математики XX в., о науке, ведущей свои изыскания в абсолютно новой области с неизведанными перспективами. Он подчеркнул, что наука XX в. не боится атаковать основы построений, которые столь долго казались непоколебимыми.

^* (Дарбу Гастон (1842-1917) - французский математик, автор работ по дифференциальной геометрии, теории дифференциальных уравнений и другим областям математики.)

Позднее идеи, приведшие к созданию меры и интеграла Лебега, позволили А. Н. Колмогорову построить аксиоматику теории вероятностей, а Норберту Винеру - определить понятия меры и интеграла для пространств, состоящих из функций. Всюду, куда проникали идеи меры, использовались конструкции и теоремы, восходящие к Лебегу. После упомянутых выше работ А. Н. Колмогорова эти идеи стали широко использоваться в теории вероятностей и ее приложениях, в частности в статистической физике. Применялись они и при изучении динамических систем. А уж о теоретической математике не приходится и говорить - без интеграла Лебега многие ее важнейшие результаты невозможно даже и сформулировать. Недаром в гимне "Лузитании" - группы молодых советских математиков, посвятивших себя в 20-е годы изучению новейшей теории функций, пелось: "Наш бог - Лебег, Кумир наш - интеграл". Но о "Лузитании" названной в честь общего учнтеля этих математиков, основателя русской школы теории функций действительного переменного Николая Николаевича Лузина, надо сказать подробнее - ее роль в изучении математических проблем, связанных с бесконечными множествами, трудно переоценить.

"Лузитания". После описанных выше работ, приведших к созданию новой теории функций, интерес к этой теории необычайно возрос во всем мире. В Геттингене Д. Гильберт и его ученики применяли новое понятие интеграла для изучения круга вопросов, связанных с так называемыми интегральными уравнениями, ряд интереснейших теорем доказали итальянские математики.

В XIX в. общепризнанным центром русской науки был Петербург, где в стенах Петербургской академии наук свято хранили традиции Эйлера и Д. Бернулли, где трудились замечательные русские математики М. В. Остроградский^* и П. Л. Чебышев^**, А. А. Марков^*** и А. М. Ляпунов^****, В. А. Стеклов^***** и А. Н. Коркин^******. Всех их объединяла искренняя любовь к исследованиям в области математического анализа и его приложений, к решению трудных конкретных проблем математики. А вот новомодные исследования по теории множеств и теории разрывных функций никакого отклика в их сердцах не находили. Слишком далекими казались им эти исследования от тех задач, которыми они занимались (хотя впоследствии полученные на этих новомодных путях результаты оказались полезными как раз во многих традиционных областях математики).

^* (Остроградский Михаил Васильевич (1801-1862) - русский математик, один из основателей петербургской математической школы, автор выдающихся работ по уравнениям математической физики, математическому анализу, теоретической механике.)

^** (Чебышев Пафнутнй Львович (1821-1894) - русский математик и механик, основатель петербургской математической школы, автор замечательных работ по математическому анализу, теории чисел, теории вероятностей, теории механизмов.)

^*** (Марков Андрей Андреевич (1856-1922) - русский математик, автор выдающихся работ по теории чисел, математическому анализу, теории вероятностей.)

^**** (Ляпунов Александр Михайлович (1857-1918) - русский математик и механик, автор выдающихся работ в области теории потенциала, устойчивости движения, теории равновесия фигур вращающейся жидкости, теории вероятностей.)

^***** (Стеклов Владимир Андреевич (1864-1926) - русский и советский математик, автор выдающихся работ по математической физике.)

^****** (Коркин Александр Николаевич (1837-1908) - русский математик, автор работ по теории чисел и по уравнениям в частных производных.)

Иначе сложилось дело в древней столице России. Здесь в стенах прославленного Московского университета уже в начале XX в. стали читаться курсы по теории множеств, а в 1907 г. московский ученый И. И. Жегалкин^* защитил магистерскую диссертацию по трансфинитным числам. Внимание этому кругу вопросов уделил и один из крупнейших московских математиков того времени Д. Ф. Егоров^**, хотя основным делом его жизни были исследования по дифференциальной геометрии. Ему удалось доказать теорему о сходимости рядов, которая стала одним из важнейших орудий во всех исследованиях по теории функций. По самое главное было в том, что он привлек к этим исследованиям своих молодых учеников и в том числе начинавшего в те годы свою научную карьеру Н. Н. Лузина.

^* (Жегалкин Иван Иванович (1869-1947) - советский математик, автор работ по математической логике, основаниям математики, теории множеств.)

^** (Егоров Дмитрий Федорович (1869-1931) - советский математик, автор работ по дифференциальной геометрии, теории интегральных уравнений и теории функций действительного переменного.)

В это время многие ученые пытались понять, как связаны "дикие" функции, открытые Дирихле и Риманом, Борелем и Лебегом, с функциями, которыми занимались предшествующие поколения ученых. Лузин доказал, что путем "исправления" разрывной функции на множестве сколь угодно малой меры из нее можно получить непрерывную функцию. А непрерывную функцию можно с любой степенью точности приблизить многочленом. Тем самым наиболее запутанно устроенные функции в некотором смысле слова сводились к наиболее изученным - многочленам.

Одновременно с этим Лузин изучал проблемы, связанные с тригонометрическими рядами,- вопросом, который традиционно интересовал специалистов по теории функций действительного переменного еще со времен самых первых работ Кантора. Здесь он также доказал ряд интереснейших теорем, выявивших тонкие механизмы, управляющие сходимостью таких рядов. Эти и многие другие доказанные Лузиным теоремы легли в основу представленной им на соискание ученой степени магистра чистой математики диссертации "Интеграл и тригонометрический ряд". Научные достоинства этой диссертации были настолько высоки, что, несмотря на сопротивление некоторых математиков классического направления, ему была присуждена сразу ученая степень доктора чистой математики - случай, весьма редкий в практике русских университетов.

Научный энтузиазм Лузина, новизна его идей, незаурядный педагогический талант привлекали к нему многих наиболее талантливых молодых математиков, большинство из которых примкнуло к нему еще на студенческой скамье. Многие из них еще до окончания университета получили крупные научные результаты. Многие годы ученые пытались доказать, что если тригонометрический ряд сходится к нулю почти всюду (то есть всюду, кроме множества нулевой меры), то все его коэффициенты равны нулю. Ко всеобщему изумлению студент Дмитрий Евгеньевич Меньшов^* показал, что это не так. Построенный им пример был весьма замысловат, как и многие примеры, которые с таким блеском строил и сам Николай Николаевич, и его ученики. С работы Меньшова начался ряд исследований по открытой им проблематике. Сильные результаты получила в этой области Нина Карловна Бари^**, которая позднее написала прекрасную книгу о тригонометрических рядах. Рядом вопросов теории таких рядов занимался в студенческие годы Андрей Николаевич Колмогоров. Ему принадлежит удивительный пример интегрируемой по Лебегу функции, для которой соответствующий тригонометрический ряд всюду расходится.

^* (Меньшов Дмитрий Евгеньевич (р. 1892) - советский математик, автор выдающихся работ по теории тригонометрических и ортогональных рядов.)

^** (Бари Нина Карловна (1901-1961) - советский математик, автор работ по теории тригонометрических рядов.)

Другое направление работ учеников Лузина было связано с исследованием строения борелевских множеств. Чтобы доказать, что любое такое множество либо счетно, либо содержит подмножество мощности континуума, Павел Сергеевич Александров придумал еще на студенческой скамье остроумнейшую конструкцию, с помощью которой можно было получить любое такое множество (в его честь ее называют теперь A-операцией). Через некоторое время другой молодой ученик Лузина, Михаил Яковлевич Суслин^*, доказал, что с помощью A-операций можно получать и некоторые множества, не являющиеся борелевскими. Возник вопрос об описании этого класса множеств, называемых теперь суслинскими. К сожалению, безвременная смерть от сыпного тифа в 1919 г. прервала исследования Суслина. Решением возникших проблем занялся сам Лузин, к которому потом примкнули Петр Сергеевич Новиков^** и Людмила Всеволодовна Келдыш^***. Полученные ими результаты стали основой, на которой выросло новое направление математики - дескриптивная теория множеств. Дальнейшие исследования в этом направлении гутронули самую сущность основ теории множеств, показали границы теоретико-множественного мышления. Многие из проблем, решенных в настоящее время, были поставлены в работах Лузина, причем получаемые результаты подтверждают его глубокие предвидения.

^* (Суслин Михаил Яковлевич (1894-1919) - русский математик, один из создателей дескриптивной теории множеств.)

^** (Новиков Петр Сергеевич (1901-1975) - советский математик, автор выдающихся работ по дескриптивной теории множеств и математической логике.)

^*** (Келдыш Людмила Всеволодовна (1904-1976) - советский математик, автор работ по дескриптивной теории множеств.)

Большое внимание уделял Лузин приложению своих идей к вопросам классического анализа, в частности, к теории функций комплексного переменного.

В результате деятельности Лузина и его учеников Москва стала общепризнанным центром научных исследований в области теории функций действительного переменного. Этому не смогли помешать ни первая мировая и гражданская войны, ни интервенция, ни блокада. В Польше идеи Лузина развивал Вацлав Серпинский^*, который в годы первой мировой войны жил в Москве и общался с Лузиным.

^* (Серпинский Вацлав (1882-1969) - польский математик, основатель польской математической школы. Автор работ по теории функций действительного переменного, топологии, теории чисел.)

Можно было бы назвать многих и многих учеников Лузина, большинство из которых являются славой и гордостью советской науки. Многие из них стали впоследствии действительными членами и членами-корреспондентами АН СССР, математиками с мировой известностью. Так возникла одна из самых замечательных научных школ, которая, как уже говорилось выше, получила по имени своего основателя и главы название "Лузитания". Это было сообщество молодых математиков, связанных друг с другом горячей любовью и живым бескорыстным интересом к математической науке.

Следует отметить, что из-за чрезмерной поглощенности проблемами теории множеств и функций действительного переменного лузитане иногда недооценивали важность классических направлений в математике. Но впоследствии научные интересы многих из них сдвинулись в области, лежавшие гораздо ближе к практическим задачам. Например, как уже упоминалось, А. Н. Колмогоров применил идеи лебеговой меры в теории вероятностей, а потом стал заниматься практическими приложениями этой теории. Даже такой видный представитель прикладной математики, как Михаил Алексеевич Лаврентьев^*, в молодые годы занимался тончайшими исследованиями по теории множеств.

^* (Лаврентьев Михаил Алексеевич (1900-1980) - советский математик и механик, один из основателей Сибирского отделения АН СССР. Автор выдающихся работ в области теории функций, квазиконформных изображений, аэро- и гидродинамики.)

Большие ирригационные работы. Проследить в рамках этой книги за всеми областями математики, которыми стали заниматься бывшие лузитане, совершенно невозможно - для этого надо было бы написать книгу по истории советской математики. Мы расскажем лишь о том, как идеи теории бесконечных множеств были применены в топологии - науке о свойствах фигур, остающихся неизменными при преобразованиях самого общего вида. Надо только, чтобы эти преобразования были взаимно однозначными и чтобы не было ни разрывов, ни склеек. Первоначально топологи изучали лишь фигуры, которые можно разбить на конечное число простейших фигур, называемых симплексами (точек, отрезков, треугольников, тетраэдров). Но потом они применили свои идеи к множествам гораздо более сложного строения. И тут выяснилось, что геометрическая интуиция, верно служившая им раньше, дает неверные ответы на многие вопросы.

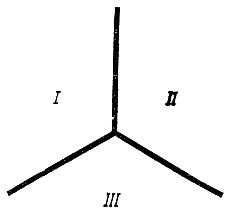
Рис. 30

Несколько удивительных примеров кривых и областей на плоскости построил голландский математик Брауэр^*. Мы расскажем сейчас об одном из самых удивительных среди этих примеров. Нарисуем карту какой-нибудь страны и сопредельных с ней стран. Почти каждая точка границы этой страны принадлежит двум и только двум странам: данной и одной из сопредельных. Поэтому в каждой точке границы стоят два пограничника: один из этой страны, а другой - из сопредельной. Есть на карте несколько точек, где сходятся три страны (рис. 30). В таких точках стоят уже три пограничника. Но таких мест на карте лишь конечное число. И кажется совершенно очевидным, что такие точки не могут заполнить всю границу страны, то есть что не может быть трех областей (трех стран), имеющих одну и ту же общую границу. Иными словами, кажется очевидным, что три пограничника из трех разных стран не могут стоять в каждой точке границы.

^* (Брауэр Лёйтзен (1881 - 1966) - голландский математик, автор важных результатов в области топологии, функционального анализа, математической логики.)

А Брауэр построил такие три области. Чтобы понять этот пример, представим себе, что в океане есть остров, на котором находятся два озера с пресной водой. Только в одном озере вода холодная, а в другом - теплая. Теперь проведем следующие ирригационные работы. В течение первых суток проведем каналы от океана и от обоих озер так, чтобы каждый из этих каналов был "слепым" (то есть только заливом соответствующего водоема), чтобы эти каналы нигде не соприкасались друг с другом и чтобы в результате расстояние каждой точки суши до океанских вод, а также до вод обоих озер было меньше 1 километра (рис. 31).

Рис. 31

В следующую половину суток продолжим эти каналы так, что они по-прежнему остаются "слепыми" и не соприкасаются между собой, а расстояние от каждой точки суши до любого из трех каналов становится меньше, чем ¹/₂ километра. При этом, конечно, каналы должны стать более узкими, чем ранее. В следующую четверть суток каналы продолжаются дальше так, чтобы каждая точка суши отстояла от любого канала меньше, чем на ¹/₄ километра, и т. д. С каждым шагом каналы становятся все извилистее и извилистее, все уже и уже. Через двое суток такой работы весь остров будет пронизан этими тремя каналами и превратится в канторову линию. Стоя в любой точке этой линии, можно зачерпнуть, по желанию, соленой, теплой пресной или холодной пресной воды. При этом воды не смешиваются друг с другом, Если бы вместо океана и озер мы взяли три страны, то получили бы ту удивительную картину, о которой говорили вначале,- в каждой точке границы можно поставить трех пограничников - по одному от каждой страны.

"Недиссертабельная" тема. У канторова определения линии был один недостаток - оно совсем не годилось для пространственных кривых. А уж что такое поверхность в пространстве, определить таким образом было весьма сложно, так как и кривые, и поверхности являются континуумами без внутренних точек. Эту задачу - выяснить, чем отличаются в пространстве кривые от поверхностей,- поставил летом 1921 г. Д. Ф. Егоров перед П. С. Урысоном^* (как видно, он больше думал о математической значительности проблемы, чем, как теперь иногда говорят, о "диссертабельности" темы - задача-то была одной из труднейших!).

^* (Урысон Павел Самуилович (1898-1924) - советский математик, автор важных работ в области теоретико-множественной топологии, один из создателей общей теории размерности.)

Вскоре Урысон понял, что задача Егорова лишь частный случай гораздо более общей проблемы: что такое размерность геометрической фигуры, то есть сколько измерений она имеет, почему надо говорить, что отрезок или окружность имеют размерность 1, квадрат - размерность 2, а куб или шар - размерность 3? Вот как вспоминает об этом периоде жизни П. С. Урысона его ближайший друг П. С. Александров: "...Все лето 1921 года прошло в напряженных попытках найти "настоящее" определение (размерности), причем П. С. переходил от одного варианта к другому, постоянно строя примеры, показывавшие, почему тот или иной вариант надо отбросить. Это были два месяца действительно всепоглощающих размышлений. Наконец, в одно утро в конце августа II. С. проснулся с готовым, окончательным и всем теперь хорошо известным индуктивным определением размерности... В то же утро во время купания в Клязьме П. С. Урысон рассказал мне свое определение размерности и тут же, во время этого разговора, затянувшегося на несколько часов, набросал план всего построения теории размерности с целым рядом теорем, бывших тогда гипотезами, за которые неизвестно было, как и взяться, и которые затем доказывались одна за другой в течение последующих месяцев. Никогда потом я не был участником или свидетелем математического разговора, который состоял бы из такого сплошного потока новых мыслей, как в то августовское утро. Вся набросанная тогда программа полностью осуществилась в течение зимы 1921/22 года; к весне 1922 года вся теория размерности была готова...".

Основная идея определения размерности по Урысону заключается в следующем. Чтобы отделить часть линии от всей остальной линии обычно достаточно двух или нескольких точек (на рис. 32 часть четырехлепестковой розы, содержащая центр, отделяется от остальной розы восемью точками). Но часть поверхности уже невозможно отделить от всей поверхности несколькими точками - для этого обязательно потребуется целая линия: сколько бы точек ни взять на поверхности, их всегда можно обойти. Точно так же часть трехмерного пространства отделяется от всего остального пространства поверхностью.

Все это надо было еще уточнить: на некоторых линиях для отделения части требуется бесконечно много точек, но эти точки не образуют в совокупности никакой линии. Урысону удалось точно сформулировать все нужные определения. В каком-то смысле его определения напоминали определения Евклида (оконечность линии - точки, оконечность поверхности - линии). Но это сходство примерно такое же, как между греческой триерой и современным океанским лайнером.

Уточним эти определения. Назовем границей точечного множества A в объемлющем его точечном множестве X совокупность всех точек на X, сколь угодно близко к которым есть как точки, принадлежащие A, так и точки из X, которые A не принадлежат. Например, для квадрата на плоскости граница совпадает с его обычной границей, а для того же квадрата в пространстве - с ним самим. Множество A называется открытым в X, если оно не содержит ни одной точки своей границы в X. Примером такого множества может служить круг на плоскости, если отбросить граничную окружность.

Множество X имеет размерность нуль, если любая его тонка содержится в сколь угодно малом множестве, граница которого в X пуста. Примерами таких множеств могут служить любое конечное множество точек, точки с рациональными координатами на прямой, канторово множество и т. д.

Далее, множество X имеет размерность один, если оно не является нуль-мерным, но любая его точка может быть заключена в сколь угодно малое открытое в X множество, граница которого в X нуль-мерна.

Оказалось, что не только все обычные линии (окружности, отрезки прямых, эллипсы и т. д.) имеют размерность единица по Урысону, но и все каиторовы линии имеют ту же размерность. Поэтому можно было определить понятие не только плоской, но и пространственной линии:

Линией называется континуум размерности единица.

А теперь было уже ясно, как определять поверхности, трехмерные тела и вообще множества любой размерности. Поскольку Урысон дает сначала определение размерности 0, затем с помощью этого определения - определение размерности 1, затем точно так же - определение размерности 2 и т. д., введенное Урысоном общее определение размерности называют индуктивным.

Работу надо не рецензировать, а печатать! Урысон доказал много интереснейших теорем, связанных с введенным им понятием размерности. Но одну самую главную теорему ему никак не удавалось доказать: не получалось доказательство того, что самый обычный куб имеет размерность 3. После длительных усилий он нашел замечательный выход из положения, придумав новое определение размерности. Мы не будем детально излагать это определение, а поясним его на простейших фигурах.

Рис. 33

Если взять отрезок или окружность, то их можно разбить на сколь угодно малые части так, что каждая точка принадлежит не более чем двум кусочкам (рис. 33). При этом надо брать кусочки вместе с их границами (то есть конечными точками). Квадрат уже так разбить нельзя. На первый взгляд кажется, что при разбиении квадрата на куски всегда будут точки, принадлежащие четырем частям (рис. 34, а). Но если уложить части так, как кладут кирпичи на стройке, то удается добиться, чтобы каждая точка принадлежала не более чем трем различным частям (рис. 34, б). Точно так же у куба есть разбиение на маленькие параллелепипеды, при котором каждая точка принадлежит не более чем четырем параллелепипедам.

Рис. 34

Именно это свойство и принял Урысои за новое определение размерности. Фигура называется имеющей размерность n, если ее можно разбить на сколь угодно малые замкнутые части так, чтобы ни одна точка не принадлежала n+2 различным частям, но при любом достаточно мелком разбиении найдутся точки, принадлежащие n+1 различным частям.

Используя это определение размерности, Урысон доказал, что размерность квадрата равна 2, куба - 3 и т. д. А потом он показал, что это определение равносильно первоначально данному.

Построенная Урысоном теория размерности произвела глубокое впечатление на весь математический мир. Об этом ярко говорит следующий эпизод. Во время заграничной командировки Урысон сделал доклад о своих результатах в Геттингене. До прихода нацистов к власти Геттингенский университет был одним из основных математических центров. После доклада руководитель геттингенской математической школы знаменитый Давид Гильберт сказал, что эти результаты надо опубликовать в журнале "Mathematische Annalen" - одном из главных математических журналов того времени. Через несколько месяцев Урысон снова делал доклад в Геттингене и Гильберт спросил у своего помощника по журналу, напечатана ли уже работа Урысона. Тот ответил, что работа рецензируется. "Но я же ясно сказал, что ее надо не рецензировать, а печатать!" - воскликнул Гильберт. После столь недвусмысленного заявления статья была немедленно напечатана,

В течение трех лет продолжалась не имеющая равных по глубине и напряженности научная деятельность Урысона (за это время он опубликовал несколько десятков научных работ). Трагический случай оборвал его жизнь - он утонул 17 августа 1924 г., купаясь во время шторма в Бискайском заливе. За день до смерти он закончил очередную научную работу.

После смерти П. С. Урысона остались многочисленные черновики и наброски неопубликованных результатов. Его ближайший друг (и соавтор по многим работам) Павел Сергеевич Александров, отложив на некоторое время свои исследования, подготовил эти работы к печати, сделав тем самым и эти результаты Урысона достоянием всех математиков. В настоящее время теория размерности стала важной главой математики.