Глава 2. Тайны бесконечных множеств

Понятие без определения. О многом и едином рассуждали Пифагор и Зенон, Платон и Аристотель. Еще пифагореец Модерат определял число (разумеется, натуральное), как собрание единиц, а Евклид в VII книге "Начал" прямо пишет, что "Число же - множество, составленное из единиц" (в древнегреческой математике единица числом не считалась).

Но "теоретико-множественный бум", то есть широкое использование теории множеств в самых разных областях науки и техники, возник только в XX в. Почему же раньше обходились без этого понятия? Ответ на этот вопрос весьма несложен: те, кто раньше не знал о множествах, были подобны мольеровскому герою, не знавшему, что он говорит прозой. Они имели дело с множествами на каждом шагу, не называя их лишь по имени.

Экономист, планировавший взаимосвязи между цехами завода, не думал о каждом отдельном станке, он размышлял о всей совокупности токарных или фрезерных станков и об их производительности. Точно так же офицер, готовивший военную операцию, должен был в зависимости от своего ранга обдумывать действия роты или батальона, полка или дивизии, но не действия каждого солдата в отдельности.

Всем им приходилось работать с совокупностями некоторых объектов, изучая их как нечто целое, объединенное в один коллектив. Математик сказал бы, что они имели дело со множествами элементов, а не с отдельными элементами. К сожалению, он не смог бы ответить на вопрос, что же такое множество. Дело в том, что математики привыкли, определяя новое понятие, сводить его к другим, уже известным ранее. Но откуда-то надо начинать, а понятия более первичного, чем множество, в математике нет.

Это и неудивительно, если вспомнить, что почти любая наука начинается с классификации, с объединения в одно целое похожих объектов или понятий и с разграничения непохожих вещей. До того, как возникла биология, люди должны были научиться отличать друг от друга волков и шакалов, зайцев и кроликов. А до создания минералогии надо было много столетий собирать камни и отличать друг от друга граниты и кремни, малахиты и яшмы. Но каждая классификация с точки зрения математики сводится к образованию множеств по некоторым признакам. Поэтому и нельзя свести понятие множества к более простым. Мы ограничимся лишь тем, что приведем еще несколько примеров множеств.

Можно говорить, например, о множестве стульев в данной комнате, о множестве всех протонов на Юпитере, о множестве слов, встречающихся в произведениях А. С. Пушкина, о множестве всех клеток человеческого тела, о множестве всех рыб в океане, о множестве всех натуральных чисел, о множестве всех точек на плоскости, о множестве всех сфер в пространстве и т. д.

Объекты или понятия, из которых составлено данное множество, называются его элементами. Приведенные выше примеры показывают, что этими элементами могут быть как реальные объекты (стулья, протоны, рыбы и т. д.), так и абстрактные понятия (числа, точки, геометрические фигуры и т. д.). В качестве элементов множеств могут выступать даже такие создания человеческой фантазии, как мифологические герои, привидения и боги всевозможных религий.

Если множество состоит из реальных объектов, оно, как правило, конечно, то есть содержит конечное число элементов. Конечные множества обычно задают списком их элементов. Например, множество дней недели задается списком

{понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}.

Разумеется, конечные множества, содержащие слишком много элементов, задать списком невозможно - вряд ли кому-нибудь удастся "переписать" всех рыб в океане или все песчинки на берегу моря.

Конечными могут быть и множества, состоящие из абстрактных понятий или мифологических героев и богов (например, конечны множества четных простых чисел, олимпийских богов и т. д.). А множество натуральных чисел бесконечно, так же как и множество точек на плоскости.

Фигурные скобки, в которые заключен список элементов множества, символизируют объединение этих элементов в одно целое. При этом принадлежность элемента а множеству А записывают с помощью знака ∈: а∈А. Если нее элемент а не принадлежит множеству А, то пишут, что а∈А. Например, если обозначить буквой N множество натуральных чисел, то 6∈N, а ³/₄∉N и крокодил ∉N. Если А - множество всех месяцев в году, то май ∈A, а среда ∉A.

Итак, говоря о множестве, мы объединяем некоторые элементы или понятия в одно целое и в дальнейшем оперируем этим целостным понятием. Основатель теории множеств немецкий математик Георг Кантор^* выразил это так: "Множество есть многое, мыслимое нами как единое".

^* (Кантор Георг (1845-1918) - немецкий математик, создатель теории множеств.)

Для того чтобы наглядно представить себе понятие множества, один из основателей русской теоретико-множественной школы академик Н. Н. Лузин^* предложил следующий образ. Представим прозрачную непроницаемую оболочку, нечто вроде плотно закрытого прозрачного мешка. Предположим, что внутри этой оболочки заключены все элементы данного множества А и что, кроме них, никаких элементов там не находится. Эта оболочка с находящимися внутри нее предметами и может служить образом множества А, состоящего из этих элементов. Сама же прозрачная оболочка, охватывающая все элементы множества, и только их, изображает тот акт объединения элементов, в результате которого создается множество А.

^* (Лузин Николай Николаевич (1883-1950) - советский математик, один из основателей Московской математической школы, автор ряда выдающихся работ по теории множеств и теории функций действительного переменного.)

Множества и свойства объектов. Ни бесконечные множества, ни конечные множества, содержащие очень много элементов, невозможно задать с помощью списков. Чтобы определить такое множество, прибегают к указанию свойства, присущего всем его элементам, но не присущего ни одному элементу, не принадлежащему определяемому множеству. Это свойство элементов множества называется для него характеристическим.

Например, для множества простых чисел характеристическим является то, что все его элементы - натуральные числа, имеющие ровно два делителя. Пользуясь этим свойством, можно сразу сказать, что ни число 1, ни число 18, ни, наконец, число ²/₃ не являются простыми. Число 1 потому, что оно имеет лишь один, а не два различных делителя, число 18 потому, что у него шесть различных делителей: 1, 2, 3, 6, 9, 18, а число ²/₃ потому, что оно не является натуральным. Число же 7 является простым, так как оно имеет ровно два делителя: числа 1 и 7.

В древности философы усиленно искали характеристические свойства различных множеств. Например, знаменитому древнегреческому философу Платону приписывали следующее определение: "Человеком называется двуногое живое существо, лишенное перьев". Рассказывают, что его современник Диоген ощипал петуха и сказал: "Вот человек Платона". Пришлось Платону добавить к своему определению слова "и с широкими ногтями". Теперь уже получилось характеристическое свойство для множества людей, которое, впрочем, никак не раскрывало истинную сущность понятия человек.

Если слова "элемент x обладает свойством P>> обозначить для краткости P(x), то множество элементов, обладающих этим свойством, обозначают {x| P(x)}. Например, множество A = {x|x²-3x+2 = 0} состоит из всех корней уравнения x²-3x+2 = 0, а множество B = {x|x∈N и 0<x<3} - из натуральных чисел, удовлетворяющих неравенству 0<x<3. Оба эти множества состоят из чисел 1 и 2, то есть состоят из одних и тех же элементов. Такие множества называют равными и пишут A = B = {1, 2}. Этот пример показывает, что, хотя понятия множества и его характеристического свойства тесно связаны друг с другом, они отнюдь не являются тождественными - одно и то же множество может задаваться различными характеристическими свойствами. Характеристические свойства, задающие одно и то же множество, называют обычно равносильными.

Во многих математических теоремах речь идет о совпадении двух множеств, например множества натуральных чисел, делящихся на 3, и множества натуральных чисел, сумма цифр десятичной записи которых делится на 3, или множества равносторонних треугольников и множества равноугольных треугольников. В некоторых случаях проблема совпадения или различия двух множеств, заданных своими характеристическими свойствами, не решена до сих пор. Например, неизвестно, совпадает ли множество натуральных чисел n, для которых уравнение xⁿ + yⁿ = zⁿ имеет решение в натуральных числах, с множеством {1,2} (так называемая великая теорема Ферма), совпадает ли множество простых чисел p, для которых 2^p-1 делится на p², с множеством {1093, 3511} и т. д.

Множества и реальный мир. Мы уже говорили, что элементами множеств могут быть объекты самого различного вида. Специалисты в тех или иных областях науки имеют дело с множествами предметов и понятий, рассматриваемых в этих науках. Сейчас теоретико-множественные методы используются и в лингвистике, и в этнографии, и в физике. Лингвисты рассматривают, например, множество глаголов или множество падежей данного языка, этнографы - множество видов родственных отношений для членов данного племени, физики - множество молекул газа в данном объеме.

Все эти множества конечны и потому во многих случаях могут быть заданы своими перечнями. Например, учитель, изучая успеваемость в каком-нибудь классе средней школы, задает множество учеников этого класса их списком в классном журнале, библиотекарь задает списком (каталогом) множество книг в библиотеке, географ задает списком множество государств на земном шаре.

По мере развития физики элементарных частиц оказывается все более сложным делом описывать эти частицы на языке теории множеств, поскольку они все время превращаются друг в друга, причем из протона может получиться нейтрон, а из нейтрона - снова протон, так что слова "состоит из" утрачивают свой наглядный смысл.

При составлении множеств из объектов реального мира приходится обычно отождествлять те или иные предметы или понятия. Например, говоря о множестве слов русского языка, составитель словаря пренебрегает тем, что эти слова по-разному произносятся в разных областях страны. Для него эти варианты произношения несущественны и задают один и тот же элемент множества русских слов. По-иному подходят к тому же множеству диалектологи, для которых наиболее интересны именно различные варианты произношения.

Таким образом, говоря об элементах того или иного множества (как состоящего из реальных объектов, так и составленного из абстрактных понятий), мы осуществляем некоторую операцию отождествления, интуитивно чувствуя, что в данном случае она не приведет к противоречию. Иными словами, множества возникают из более расплывчатых понятий путем отождествления тех или иных элементов.

Другие осложнения при использовании теоретико-множественных понятий для изучения реального мира возникают из-за расплывчатости, нечеткости многих понятий, недостаточной определенности многих свойств предметов, трудности расчленения действительности на отдельные объекты. О некоторых из этих осложнений будет рассказано далее.

Разумеется, все указанные осложнения не могут послужить причиной для отказа от использования теоретико-множественного языка при описании действительности, при построении научных теорий. Они указывают лишь на то, что теоретико-множественная трактовка той или иной области наук налагает серьезные ограничения на наш подход к изучаемым явлениям, приводит во многих случаях к определенному "огрублению" этих явлений.

В то же время, как указывает Ю. И. Манин^*, понятия теории множеств весьма полезны при построении математических моделей явлений реального мира, так как они дают универсальную базу для определения всех математических конструкций на основе "обобщенно геометрических образов". Он пишет, что эти образы представляют собой вместилище смысла математических формализмов и в то же время средство для отбора содержательных утверждений из всего необозримого моря выводимых математических формул. Поэтому такие образы выступают в роли естественного посредника между математикой и физикой. По его мнению, теоретико-множественный язык хорош тем, что он не вынуждает говорить ничего лишнего.

^* (Манин Юрий Иванович (р. 1937) - советский математик, автор работ по алгебре и приложениям математики к современной физике.)

Множества и язык. Мы уже отмечали, что задание множеств реальных объектов с помощью их характеристических свойств наталкивается на затруднения. Эти затруднения связаны как с большим числом промежуточных форм, так и с недостаточной четкостью обыденного языка. Казалось бы, например, что множество русских слов однозначно определено и всем ясно, что ему принадлежат слова воин, конь, стоять и не принадежат слова table, legen, απειρον. Однако, раскрыв семнадцатитомный словарь русского языка, многие читатели встретят там незнакомые слова, принадлежность которых этому множеству им не была ранее известна. Кроме того, на протяжении веков в русском языке появлялись новые слова, иногда заимствованные из других языков, например хозяин или амбар - из тюркских языков, зонтик - из голландского, периферия - из греческого, другие же слова отмирали и исчезали.

Никто теперь не скажет кмети вместо воины, забыто и не применяется слово смерды, долгие споры ведут ученые о том, что значило слово харалужный. И всегда существовали слова, относительно которых не было уверенности, вошли ли они уже в словарный состав русского языка или, наоборот, сохранились ли они еще в нем. Например, в начале XIX в. адмирал А. С. Шишков отвергал такие слова, как галоши и , предлагая заменить их на мокроступы и окоем, а в середине того же века много спорили о том, следует ли сохранять в литературной речи слова сей и оный или они уже устарели. Как пишет в своих воспоминаниях писатель Юрий Трифонов, тонкий знаток русской речи К. А. Федин употреблял слова заочный и заочник, лишь взяв их в кавычки, поскольку считал, что они чересчур новомодны.

По указанным причинам многие ученые предпочитают не считать совокупность русских слов множеством. В то же время русские слова, содержащиеся в том же семнадцатитомном словаре, несомненно, образуют множество - о каждом слове можно наверняка сказать, встречается оно в этом словаре или нет.

Не является вполне определенным термин множество планет Солнечной системы. Не говоря уже о том, что мы не знаем сейчас, существуют ли планеты за Плутоном, надо иметь в виду, что кроме больших планет - Меркурия, Венеры, Земли, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона - вокруг Солнца обращается около 1600 малых планет, так называемых астероидов. Поперечники некоторых из них, например Цереры, Паллады, Юноны, измеряются сотнями километров, но есть и астероиды, поперечники которых не превышают 1 км. По мере улучшения методов наблюдения астрономы будут открывать небесные тела все меньших размеров, и наконец возникнет вопрос, где же кончаются планеты и начинаются метеориты и космическая пыль.

Впрочем, разница между планетами и метеоритами интересует в основном астрономов и не столь уже важна. Но для юриста разница между грабежом, кражей со взломом, похищением и другими видами преступлений является существенно важной - от той или иной квалификации преступления зависит приговор суда. Поэтому при формулировке законов и постановлений всегда стремятся к четким и недвусмысленным определениям для всех встречающихся в них понятий. Например, определяя, кто имеет право бесплатного проезда по железным дорогам СССР, пишут не "маленькие дети", а "дети до пяти лет". Тем самым четко определено, кто из детей имеет это право, а кто нет. Единственным исключением является случай, когда малолетнему пассажиру доведетcя праздновать день рождения в пути^* но это настолько маловероятно, что правила об этом ничего не говорят. Правда, рассказывают, что один пунктуальный отец включил стоп-кран в момент, когда его сыну исполнилось пять лет, чтобы точно определить оставшийся отрезок пути, за который следовало уплатить.

^* (Заде Лотфи (р. 1918) - американский математик, создатель теории нечетких множеств.)

Нечеткие множества. Оригинальный выход из описанных выше затруднений предложил американский ученый Л. Заде^*: он ввел понятие нечеткого (или иначе размытого) множества и тесно связанное с ним понятие лингвистической переменной. Подобно тому как четким свойствам (быть простым числом, быть треугольником) соответствуют обычные или, иначе, четкие множества (множество простых чисел, множество треугольников), нечетким свойствам (например, быть молодым человеком, быть длинной улицей) соответствуют нечеткие множества (молодых людей, длинных улиц). Ведь, например, почтенный академик назовет молодым и сорокалетнего коллегу, а студенту-первокурснику профессор такого возраста кажется пожилым. Каждому человеку (или, точнее, каждому эксперту) соответствует четкое множество людей, которых он считает молодыми. Но тогда каждому человеку x соответствует число m/n, где n - общее число экспертов, а m - число экспертов, считающих, что x молод. Обозначим m/n через p (x) и скажем, что x входит в нечеткое множество молодых людей с коэффициентом принадлежности p(x), который, конечно, принимает значения от 0 до 1.

^* (Заде Лотфи (р. 1918) - американский математик, создатель теории нечетких множеств.)

Четкие множества отличаются от нечетких тем, что для них p(x) может принимать лишь два значения: 0 и 1, причем p(x) = 1, если x∈A, и p(x) = 0, если x∉A. Наличие экспертов позволяет из совокупности четких множеств составить нечеткое множество. Конечно, при всей нечеткости полученного множества можно с уверенностью сказать, что для некоторых x имеем p(x) = 1 (например, никто не усомнится в молодости новорожденного ребенка), а для некоторых x имеем p(x) = 0 (например, вряд ли кто-нибудь назовет молодым восьмидесятилетнего старца). Впрочем, рассказывают, что когда гроссмейстеру Тартаковеру было 65 лет, он победил 70-летнего гроссмейстера Бернштейна и воскликнул: "Молодость побеждает!".

Разумеется, созывать каждый раз консилиум экспертов для определения "коэффициентов принадлежности" вряд ли целесообразно. Чаще коэффициенты вводят иным путем, например на основе статистических данных. Но после того, как они выбраны, с их помощью можно получить коэффициенты принадлежности и для других множеств.

На основе понятия нечеткого множества были введены нечеткие отношения и нечеткие алгоритмы. С нечеткими алгоритмами люди имели дело задолго до того, как их определил Л. Заде. В любой поваренной книге найдутся алгоритмы, содержащие советы вида: "Сливки сперва особо взбить, чтобы были весьма густы, потом всыпать в них муку и еще все вместе венчиком хорошенько взбить...". И хотя авторы этих книг не определяли точно, когда сливки надо считать весьма густыми и какое взбивание венчиком надо считать достаточным, надо думать, что блюда по этим рецептам получались совсем неплохими. Любопытно, что теперь нечеткие алгоритмы начали встречаться и в таких разделах науки, как вычислительная математика. Однако только будущее покажет, был ли удачен предложенный Заде метод введения нечетких множеств и какая из него получится польза.

Бесконечные множества. Все то, что говорилось о множествах выше, относилось в основном к множествам, содержащим конечное число элементов. На протяжении тысячелетий изучение бесконечных множеств было изгнано из науки авторитетом Аристотеля. Впрочем, преподававший в Оксфордском университете в XIII в. схоласт Роберт Гроссетет (он был, между прочим, учителем знаменитого Роджера Бэкона) считал, что актуально-бесконечное - это определенное число, которое хотя и не познаваемо для нас, но существует актуально. Более того, Гроссетет считал возможным сравнивать друг с другом две бесконечности. Он полагал, что больше моментов в большем времени, чем в меньшем, и больше точек в большей величине, чем в меньшей. Число "точек в отрезке длиной в локоть" он считал истинной мерой этого отрезка. Тем самым потенциальной бесконечности Аристотеля снова была противопоставлена актуальная бесконечность единиц.

Использование актуальной бесконечности в математике исподволь начинается в XVIII в. (бесконечные ряды фактически рассматривались как суммы бесконечного множества слагаемых), а в XIX в. Гаусс, столь резко возражавший против использования актуальной бесконечности в математике, фактически использует ее в своих теоретико-числовых исследованиях. В более явном виде использование этих же понятий встречается в работах последователей Гаусса немецких математиков Л. Дирихле^* и Р. Дедекинда^**.

^* (Дирихле Лежен (1805-1859) - немецкий математик, автор работ по теории чисел, математической физике, теории рядов.)

^** (Дедекинд Рихард (1831-1916) - немецкий математик, один из создателей современной алгебры. В своих работах близко подошел к идеям теории множеств.)

Однако систематически свойства бесконечных множеств почти не изучались. Лишь в 1851 г. была посмертно опубликована книга чешского математика и философа Б. Больцано^* "Парадоксы бесконечности", в которой он сделал первую попытку исследовать свойства актуальной бесконечности. В этой книге были предвосхищены многие понятия теории бесконечных множеств, однако они не получили еще той точности и ясности, которая была придана им через два десятилетия в работах Г. Кантора.

^* (Больцано Бернард (1781-1848) - чешский математик, философ и логик, автор ряда работ по основам математического анализа и теории бесконечных множеств.)

Занимаясь теорией бесконечных рядов, составленных из тригонометрических функций, Кантор пришел к необходимости разобраться в том, какие множества можно составлять из точек прямой линии (эти множества называют теперь точечными). В частности, его заинтересовал вопрос, всегда ли можно перенумеровать все точки таких множеств. Исследуя его, он обнаружил, что свойства конечных и бесконечных множеств совершенно непохожи друг на друга: многие операции, невозможные для конечных множеств, без труда выполняются для бесконечных. Попробуйте, например, поместить в гостиницу, каждый номер которой занят одним постояльцем, еще жильцов, да так, чтобы в каждом номере снова жил лишь один человек. Не получается? Так это только потому, что число номеров в гостинице конечно! А если бы в ней было бесконечно много номеров?.. Но такие гостиницы могут встретиться разве что в рассказах межзвездного скитальца Иона Тихого. Итак, предоставим ему слово.

Необыкновенная гостиница или тысяча первое путешествие Иона Тихого. Домой я вернулся довольно поздно - вечер воспоминаний в клубе "Туманность Андромеды" затянулся далеко за полночь. Всю ночь меня мучили кошмары. То мне снилось, что меня проглотил огромный курдль, то грезилось, что я снова лечу на планету Дурдиотов и не знаю, как избежать тамошней страшной машины, превращающей людей в шестиугольники, то... Неожиданный телефонный звонок вернул меня в мир реальности. Звонил старый друг и коллега по межзвездным странствиям профессор Тарантога.

"Срочное задание, дорогой Йон,- услышал я.- Астрономы обнаружили в космосе какой-то странный объект - от одной галактики до другой тянется таинственная черная линия. Никто не понимает, в чем дело. Самые лучшие радиотелескопы, нейтриноскопы и гравитоскопы пе могут помочь в раскрытии тайны. Осталась надежда лишь на тебя. Срочно вылетай в направлении туманности АЦД-1587".

На другой день я получил из ремонта свою старую фотонную ракету, установил на нее ускоритель времени и электронного робота, знавшего все языки космоса и все рассказы о звездопроходцах (это гарантировало от скуки), и вылетел по заданию.

Когда робот исчерпал весь свой запас рассказов и начал повторяться (нет ничего хуже, чем электронный робот, десятый раз повторяющий старую историю), вдали показалась цель моего путешествия. Туманности, застилавшие таинственную линию, оказались позади, и предо мною предстала... гостиница "Космос".

Выяснилось, что межзвездные скитальцы выгонты, которым я когда-то соорудил небольшую планету, растащили и ее на мелкие части и вновь остались без пристанища. Тогда, чтобы больше не скитаться по чужим галактикам, они решили построить грандиозное сооружение - гостиницу для всех путешествующих по космосу. Эта гостиница протянулась через почти все галактики. Говорю "почти все", потому что выгонты демонтировали некоторые необитаемые галактики, а из каждой оставшейся утащили по нескольку плохо лежавших созвездий.

Но гостиницу они отстроили на славу. В каждом номере были краны, из которых текла холодная и горячая плазма. При желании можно было на ночь распылиться, а утром портье собирал постояльцев по их атомным схемам.

А самое главное, в гостинице было бесконечно много номеров. Выгонты надеялись, что теперь никому больше не придется слышать порядком надоевшую им за время скитаний фразу: "Свободных номеров нет".

Тем не менее мне не повезло. Когда я вошел в вестибюль гостиницы, первое, что бросилось в глаза, был плакат: "Делегаты съезда космозоологов регистрируются на 127-м этаже".

Так как космозоологи приехали из всех галактик, а их бесконечное множество, то все номера оказались занятыми участниками съезда. Для меня места уже не хватило. Администратор пытался, правда, поселить меня с кем нибудь из космозоологов. Но когда я выяснил, что один предполагаемый сосед дышит фтором, а другой считает нормальной для себя температуру окружающей среды 860°, то вежливо отказался от столь "приятного" соседства.

К счастью, директором гостиницы был выгонт, хорошо помнивший услуги, которые я когда-то оказал этому племени. Он постарался устроить меня в гостинице - ведь, ночуя в межзвездном пространстве, можно было схватить воспаление легких. После некоторых размышлений он обратился к администратору и сказал:

- Поселите его в № 1.

- Куда же я дену жильца этого номера? - удивленно спросил администратор.

- А его переселите в №2. Жильца же из № 2 отправьте в № 3, из № 3 - в № 4 и т. д.

Тут только я оценил необыкновенные свойства гостиницы. Если бы в ней было лишь конечное число номеров, то жителю последнего номера пришлось бы перебраться в межзвездное пространство. А из-за того, что гостиница имела бесконечно много номеров, всем хватило места, и мне удалось вселиться, не лишив жилища никого из космозоологов.

Я не удивился, когда на другое утро мне предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить еще 999 999 жильцов. Но когда на третий день пребывания в гостинице я зашел к администратору заплатить за номер, у меня потемнело в глазах. К окошку тянулась очередь, конец которой терялся где-то около Магеллановых облаков. Слышались голоса:

"Меняю две марки туманности Андромеды на марку Сириуса!"

"У кого есть марка Кита 57-го года космической эры?"

В недоумении я обратился к администратору и спросил:

- А это кто такие?

- Межгалактический съезд филателистов.

- И много их?

- Бесконечное множество - по одному представителю от каждой галактики.

- Но как же их разместят, ведь космозоологи выедут только завтра?

- Не знаю, об этом сейчас будут говорить на пятиминутке у директора.

Однако задача оказалась весьма сложной, и пятиминутка (как это часто бывает и на Земле) затянулась на целый час. Наконец администратор вышел от директора и приступил к расселению. В первую очередь он приказал переселить жильца из № 1 в № 2. Мне это показалось странным, так как по имевшемуся опыту я знал, что такое переселение освобождало лишь один номер, а разместить надо было ни много ни мало, а бесконечное множество филателистов. Но администратор продолжал командовать:

- А жильца из № 2 переселите в № 4, из № 3 - в № 6, вообще из номера n - в номер 2n.

Теперь стал ясен его план: таким путем он освободил бесконечное множество нечетных номеров и мог расселять в них филателистов. В результате четные номера оказались занятыми космозоологами, а нечетные - филателистами (о себе не говорю - за два дня знакомства я так подружился с космозоологами, что был выбран почетным председателем их съезда; вместе со всеми космозоологами мне пришлось покинуть обжитый номер и переехать из № 1000000 в № 2000000). А мой знакомый филателист, стоявший в очереди 574-м, занял № 1147. Вообще филателисты, стоявшие в очереди n-ми, занимали номер 2n-1.

На другой день положение с номерами стало легче - съезд космозоологов окончился, и они разъехались по домам. Я же переехал к директору гостиницы, в квартире которого освободилась одна комната. Но то, что хорошо для постояльцев, не всегда устраивает администрацию. Через несколько дней мой гостеприимный хозяин загрустил.

- В чем дело? - спросил я его.

- Половина номеров пустует. Финансовый план не выполняется.

Я, правда, не совсем понял, о каком финансовом плане шла речь, ведь плата поступала с бесконечного множества номеров, но тем не менее дал совет:

- А Вы переселите постояльцев так, чтобы все номера оказались занятыми.

Это оказалось совсем просто сделать. Филателисты занимали лишь нечетные номера: 1, 3, 5, 7, 9 и т. д. Жильца из № 1 оставили в покое. Из № 3 переселили в № 2, из № 5 - в № 3, из № 7 - в № 4 и т. д. В результате все номера вновь оказались заполненными, хотя ни один новый жилец не въехал.

Но неприятности директора на этом не кончились. Выяснилось, что выгонты не ограничились возведением гостиницы "Космос". Неугомонные строители соорудили еще бесконечное множество гостиниц, каждая из которых имела бесконечно много номеров. При этом они демонтировали так много галактик, что нарушилось межгалактическое равновесие, а это могло повлечь за собой весьма тяжкие последствия. Поэтому им было предложено закрыть все гостиницы, кроме нашей, и вернуть использованный материал на место. Но выполнение этого приказа было затруднено, поскольку все гостиницы (в том числе и наша) были заполнены. Предстояло переселить жильцов из бесконечного множества гостиниц, каждая из которых имела бесконечно много постояльцев, в одну гостиницу, да и та была уже заполнена.

- С меня хватит! - воскликнул директор.- Сначала я в полную гостиницу поместил одного постояльца, потом еще 999 999, потом еще бесконечно много жильцов; а теперь от меня хотят, чтобы в нее вместилось еще бесконечное множество бесконечных множеств жильцов. Нет, гостиница не резиновая, пусть где хотят, там и помещают!

Но приказ есть приказ, и через пять дней надо было все подготовить к встрече новых постояльцев. Эти дни в гостинице никто не работал - все думали, как решить задачу. Был объявлен конкурс с премией - туристическим путешествием по одной из галактик. Но все предлагавшиеся решения отвергались как неудачные. Так, младший повар предложил оставить жильца из первого номера нашей гостиницы в том же № 1, из второго номера переселить в № 1001, из третьего номера - в № 2001 и т. д. После этого поселить жильцов второй гостиницы в № 2, 1002, 2002 и т. д. нашей гостиницы, жильцов третьей гостиницы - в № 3, 1003, 2003 и т. д. Проект был отвергнут, так как уже жители первых 1000 гостиниц займут все номера и некуда будет поселить жителей 1001-й гостиницы.

Мне вспомнилось по этому поводу, что, когда раболепные римские сенаторы предложили императору Тиберию переименовать в его честь месяц сентябрь в "тиберий" (предыдущие месяцы уже получили имена императоров Юлия и Августа), он язвительно спросил их: "А что же вы предложите тринадцатому цезарю?"

Неплохой вариант предложил бухгалтер гостиницы. Он посоветовал воспользоваться свойствами геометрической прогрессии и расселить постояльцев так: жителей первой гостиницы - в № 2, 4, 8, 16, 32 и т. д. (эти числа образуют геометрическую прогрессию со знаменателем 2). Жителей второй гостиницы - в № 3, 9, 27, 81 и т. д. (а эти числа образуют геометрическую прогрессию со знаменателем 3). Так же предложил он расселять и жителей остальных гостиниц. Но директор спросил его:

- А для третьей гостиницы надо использовать прогрессию со знаменателем 4?

- Конечно,- ответил бухгалтер.

- Тогда ничего не получится, ведь в четвертом номере уже живет обитатель первой гостиницы, а теперь туда же надо вселить и жителя третьей гостиницы.

Настала моя очередь показать, что не зря в Звездной академии пять лет изучают математику.

- Воспользуйтесь простыми числами! Поселите жителей первой гостиницы в № 2, 4, 8, 16,..., второй - в № 3, 9, 27, 81,..., третьей - в № 5, 25, 125, 625,..., четвертой - в № 7, 49, 343,... .- А не получится ли опять, что в один номер придется помещать двух постояльцев? - спросил директор.

- Нет! Ведь если взять два простых числа, то никакие их степени с натуральными показателями не могут оказаться равными. Если p и q - простые числа, причем p≠q, а m и n - натуральные числа, то p^m≠qⁿ.

Директор согласился со мной и тут же нашел усовершенствование предложенного способа, при котором использовались лишь два простых числа: 2 и 3. Именно, он предложил поселить жильца из m-го номера n-й гостиницы в номер 2^m3ⁿ. Дело в том, что если m≠p или n≠q, то 2^m3ⁿ≠2^p3^q. Поэтому в один и тот же номер пе поселятся двое.

Это предложение привело всех в восторг. Была решена задача, всем казавшаяся неразрешимой. Но премии не получил ни я, ни директор - при наших решениях слишком много номеров оставались пустыми (у меня такие номера, как 6, 10, 12, и вообще все номера, которые не были степенями простых чисел, а у директора номера, которые нельзя записать в виде 2^m3ⁿ). Самое лучшее решение предложил один из филателистов - президент Математической академии галактики Лебедя.

Он посоветовал сначала составить таблицу, занумеровав ее строки номерами гостиниц, а столбцы - номерами комнат. Например, на пересечении четвертой строки и шестого столбца записывается шестая комната четвертой гостиницы. Вот эта таблица (вернее, ее левая верхняя часть, так как для записи всей таблицы надо бесконечно много строк и столбцов):

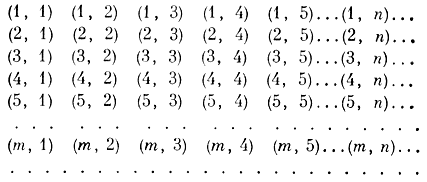
- А теперь расселяйте обитателей по квадратам,- сказал математик-филателист.

- Как?- не понял директор.

- По квадратам! В № 1 поселяется жилец из (1,1), то есть из первого номера первой гостиницы; в № 2 - из (1,2), то есть из второго номера первой гостиницы; в № 3 - из (2,2) - второго номера второй гостиницы и в № 4 - из (2,1) - первого номера второй гостиницы. Тем самым будут расселены жильцы из верхнего левого квадрата со стороной 2. После этого в № 5 поселяем жильца из (1,3), в № 6 - из (2,3), в № 7 - из (3,3), в № 8 - из (3,2), в № 9 - из (3,1). (Эти номера образуют квадрат со стороной 3.)

И, взяв листок бумаги, он набросал на нем следующую схему расселения:

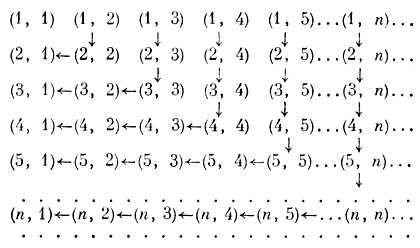
- Неужели для всех хватит места?- усомнился директор.

- Конечно. Ведь в первые n² номеров мы поселяем при этой схеме жильцов из первых п номеров первых п гостиниц. Поэтому рано или поздно каждый жилец получит номер. Например, если это жилец из № 136 гостиницы № 217, то он получит номер на 217-м шагу. Легко даже сосчитать этот номер. Он равен 217² - 136 + 1. Вообще, если жилец занимает номер n в m-й гостинице, то при n≥m он займет номер (n-1)² + m, а при n<m - номер m² - n + 1.

Предложенный проект и был признан наилучшим: все жители из всех гостиниц были поселены в нашей гостинице и ни один ее номер не пустовал. Математику-филателисту досталась премия - туристическая путевка в галактику ЛЦР-287.

В честь столь удачного размещения директор гостиницы устроил прием, на который пригласил всех ее жильцов. Этот прием также не обошелся без осложнений. Обитатели комнат с четными номерами задержались на полчаса, и, когда они появились, оказалось, что все стулья заняты, хотя гостеприимный хозяин поставил по стулу на каждого гостя. Пришлось подождать, пока все пересели на новые места и освободили необходимое количество стульев (разумеется, ни одного нового стула в зал не внесли). Зато когда стали подавать мороженое, то каждый гость получил по две порции, хотя повар заготовил в точности по одной порции на гостя. Надеюсь, что теперь читатель сам поймет, как все это случилось.

После конца приема я сел в свою фотонную ракету и полетел на Землю. Мне нужно было рассказать всем земным космонавтам о новом пристанище в космосе. Кроме того, я хотел проконсультироваться с виднейшими математиками Земли и моим другом профессором Тарантогой о свойствах бесконечных множеств.

От автора. На этом мы временно расстанемся с нашим героем. Многое в его рассказе вызывает сомнения - ведь по законам теории относительности невозможно передавать сигналы со скоростью, большей чем 300 000 ^км/_с. Поэтому даже самая первая команда администратора потребовала бы для своего выполнения бесконечно большого промежутка времени. Но не будем требовать слишком многого от Иона Тихого - в его путешествиях бывали куда более невероятные приключения.

Дальнейшая часть книги посвящается рассказу о теории бесконечных множеств. И хотя события будут развертываться не в межзвездном пространстве, а на отрезке [0, 1] или квадрате со стороной 1, многие из них окажутся не менее необычайными.

Как сравнивать множества. В начале главы мы занимались вопросами, общими для конечных и для бесконечных множеств. Теперь мы займемся свойствами, характерными только для бесконечных множеств. Из рассказа Иона Тихого уже известно, что эти свойства сильно отличаются от свойств конечных множеств - вещи, невозможные для конечных множеств, оказываются возможными для бесконечных.

Первый вопрос, который мы сейчас разберем, это вопрос о сравнении друг с другом бесконечных множеств. Для конечных множеств самой разной природы всегда можно сказать, какое из них содержит больше элементов, а какое меньше. Для бесконечных же множеств этот вопрос становится гораздо более сложным. Например, чего больше, натуральных чисел или рациональных, рациональных или действительных? Где больше точек, на отрезке или на всей прямой, на прямой или в квадрате?

На первый взгляд кажется, что ответить на эти вопросы совсем просто. Ведь множество натуральных чисел является частью множества рациональных чисел, а отрезок-частью прямой. Не ясно ли, что поэтому натуральных чисел меньше, чем рациональных, а точек на отрезке меньше, чем точек на всей прямой? Оказывается, не ясно. Ведь ниоткуда не следует, что при переходе к бесконечным множествам сохранятся .законы, выведенные из рассмотрения конечных множеств, например закон о том, что "часть меньше целого".

А самое главное, попытка сравнения бесконечных множеств по тому признаку, что одно является частью другого, заранее обречена на неудачу. Например, где больше точек, в квадрате или на всей бесконечной прямой? Ведь ни квадрат нельзя вложить в прямую линию, пи прямую линию нельзя, не ломая ее, поместить в квадрат. Разумеется, можно разломать прямую линию на отрезки, длина которых равна стороне квадрата, и после этого каждый отрезок поместить в квадрат так, чтобы они не пересекались друг с другом. Но вдруг и квадрат можно как-то разбить на части, а потом эти части положить на прямую, чтобы они не задевали друг друга? А сколько есть бесконечных множеств, не являющихся частями друг друга! Множество квадратов на плоскости и множество кругов на той же плоскости не имеют ни одного общего элемента. Как же сравнить их? Как узнать, чего больше во Вселенной - атомов азота или кислорода?

Итак, задача поставлена. В первую очередь мы выясним, в каком случае надо говорить, что одно множество содержит столько же элементов, сколько и второе. Иными словами, выясним, в каких случаях два бесконечных множества имеют "поровну" элементов.

На танцплощадке. Для конечных множеств задача сравнения решается просто. Чтобы узнать, одинаково ли число элементов в двух множествах, достаточно пересчитать их. Если получатся одинаковые числа, то, значит, в обоих множествах поровну элементов. Но для бесконечных множеств такой способ не годится, ибо, начав пересчитывать элементы бесконечного множества, мы рискуем посвятить этому делу всю свою жизнь и все же не закончить начатого предприятия.

Но и для конечных множеств метод пересчета не всегда удобен. Мы на танцплощадке. Как узнать, поровну ли здесь юношей и девушек? Конечно, можно попросить юношей отойти в одну сторону, а девушек в другую и заняться подсчетом как тех, так и других. Но, во-первых, мы получим при этом избыточную информацию, нас не интересует, сколько здесь юношей и девушек, а интересует лишь, поровну ли их. Во-вторых, не для того собралась молодежь на танцплощадке, чтобы стоять и ждать конца пересчета, а для того, чтобы потанцевать. Удовлетворим их желание и попросим оркестр сыграть какой-нибудь танец, который все умеют танцевать. Тогда юноши пригласят девушек на танец и наша задача будет решена. Ведь если окажется, что все юноши и все девушки танцуют, то есть если вся молод ежь разбилась на танцующие пары, то ясно, что на площадке ровно столько же юношей, сколько и девушек.

Совершенно тем же способом можно узнать, что число зрителей в театре равно числу театральных кресел. Если во время спектакля все места заняты, причем никто из зрителей не стоит в проходах и на каждом месте сидит один зритель, то можно быть уверенным, что зрителей ровно столько же, сколько и театральных кресел.

На каждый прилив - по отливу. Мы познакомились с тем, как узнать, что два конечных множества имеют поровну элементов, не прибегая к пересчету этих множеств. Этот способ можно применить и для бесконечных множеств. Только здесь уж не удастся прибегнуть к помощи "оркестра", а придется самим располагать элементы двух сравниваемых множеств в "танцующие пары".

Итак, пусть у нас даны два множества А и В. Говорят, что между ними установлено взаимно однозначное соответствие, если элементы этих множеств объединены в пары (a, b) так, что:

1. элемент a принадлежит множеству A, а элемент b - множеству B;
2. каждый элемент обоих множеств попал в одну и только одну пару.

Например, если множество A состоит из юношей на танцплощадке, а множество B - из девушек на той же площадке, то пары (a, b) образуются из танцующих друг с другом юноши и девушки. Если множество A состоит из зрителей, а множество B - из театральных кресел, то пара (a, b) образуется из зрителя и кресла, на котором он сидит. Читатель сам легко придумает разнообразные примеры таких соответствий между множествами равной численности.

Разумеется, не всякое соответствие между множествами является взаимно однозначным. Если множество A состоит из всех деревьев на Земле, а множество B - из растущих на них плодов, то между этими множествами можно установить соответствие: каждому плоду сопоставить дерево, на котором он растет. Но это соответствие не будет взаимно однозначным: на некоторых деревьях растет помногу плодов, а другие сейчас не плодоносят. Поэтому одни элементы a (деревья) будут участвовать во многих парах, а другие элементы a не войдут ни в одну пару.

Существование взаимно однозначного соответствия для конечных множеств равносильно тому, что у них поровну элементов. Важнейшим поворотным пунктом в теории множества был момент, когда Кантор решил применить идею взаимно однозначного соответствия для сравнения бесконечных множеств.

Иными словами, по Кантору, два (быть может, и бесконечных) множества A и B имеют поровну элементов, если между элементами этих множеств можно установить взаимно однозначное соответствие.

Обычно математики не говорят, что "множества A и B имеют поровну элементов", а говорят, что "A и B имеют одинаковую мощность" или "множества A и B эквивалентны".

Таким образом, для бесконечных множеств слово мощность значит то же самое, что для конечных множеств "число элементов".

Еще до Кантора к понятию взаимно однозначного соответствия пришел чешский ученый Б. Больцано. Но он отступил перед трудностями, к которым вело это понятие. Как мы вскоре увидим, после принятия принципа сравнения бесконечных множеств с помощью взаимно однозначного соответствия пришлось расстаться со многими догмами.

Равна ли часть целому? Основной догмой, которую пришлось отбросить, было положение, установленное на самой заре развития математики: часть меньше целого. Это положение безусловно верно для конечных множеств, но для бесконечных множеств оно уже теряет силу. Вспомните, как расселил директор необыкновенной гостиницы космозоологов по четным номерам. При этом расселении жилец из № n переезжал в № 2n. Иными словами, расселение шло по следующей схеме:

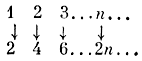
Но эта схема устанавливает взаимно однозначное соответствие между множеством натуральных чисел

и его частью - множеством четных чисел

А мы договорились считать, что множества, между которыми можно установить взаимно однозначное соответствие, содержат поровну элементов. Значит, множество натуральных чисел содержит столько же элементов, сколько и его часть - множество четных чисел.

Точно так же можно установить взаимно однозначное соответствие между множеством натуральных чисел и множеством чисел вида

Для этого надо сопоставить каждому натуральному числу n число 10ⁿ:

Этим желаемое взаимно однозначное соответствие и устанавливается. Аналогично устанавливается взаимно однозначное соответствие между множеством натуральных чисел и множеством всех квадратов натуральных чисел:

или множеством всех кубов натуральных чисел:

и т. д.

Вообще между множеством всех натуральных чисел и любой его бесконечной частью всегда можно установить взаимно однозначное соответствие. Для этого достаточно перенумеровать по порядку числа из этой части.

Впрочем, пе зря говорят, что ничто не ново под лупой, а новое - это только хорошо забытое старое. Еще в начале XVII в. Галилей размышлял о противоречиях бесконечного и обнаружил возможность взаимно однозначного соответствия между множеством натуральных чисел и множеством их квадратов. В его книге "Беседы и математические доказательства, относящиеся к механике по местному движению" (1638 г.) приведен диалог, в котором Сальвиати, выражающий мысли самого Галилея, говорит:

"Сказанное нами относится к числу затруднений, происходящих вследствие того, что, рассуждая нашим ограниченным разумом о бесконечном, мы приписываем последнему свойства, известные нам по вещам конечным и ограниченным. Между тем это неправильно, так как такие свойства, как большая и меньшая величина и равенство, неприменимы к бесконечному, относительно которого нельзя сказать, что одна бесконечность больше или меньше другой или равна ей".

В подтверждение своей мысли Сальвиати отмечает, что, с одной стороны, "квадратов столько же, сколько существует корней, так как каждый квадрат имеет свой корень и каждый корень - свой квадрат; ни один квадрат не может иметь более одного корня, и ни один корень - более одного квадрата...^* При этом число корней равно количеству всех чисел вообще, потому что нет ни одного числа, которое не могло бы быть корнем какого-нибудь квадрата; установив это, приходится сказать, что число квадратов равно общему количеству всех чисел..."

^* (Здесь имеются в виду только натуральные числи.)

С другой стороны, Сальвиати отмечает, что "количество всех чисел вместе - квадратов и неквадратов - больше, нежели одних только квадратов", причем "числа квадратов непрерывно и в весьма большой пропорции убывают по мере того, как мы переходим к большим числам". В качестве единственного выхода из обнаруженного противоречия Сальвиати предлагает следующее:

"Я не вижу возможности никакого другого решения, как признать, что бесконечно количество чисел вообще, бесконечно число квадратов, бесконечно и число корней. Нельзя сказать, что число квадратов меньше количества всех чисел, а последнее больше: в конечном выводе свойства равенства, а также большей и меньшей величины не имеют места там, где дело идет о бесконечности, и применимы только к конечным количествам".

Мы видим, что Галилей, по сути дела, владел идеей взаимно однозначного соответствия и видел, что такое соответствие можно установить между множеством всех натуральных чисел и множеством квадратов, а потому эти множества можно считать имеющими одинаковое количество элементов. Понимал он и то, что для бесконечных множеств часть может быть равной целому. Но отсюда он сделал неверный вывод, что все бесконечности одинаковы: он имел дело лишь с бесконечными подмножествами натурального ряда, а их можно перенумеровать.

Галилей не мог себе представить, что множество всех точек отрезка перенумеровать нельзя (это вскоре будет показано). Подобно атомистам древности, он полагал, что отрезок складывается из поддающейся пересчету бесконечной совокупности атомов.

Счетные множества. Все множества, которые имеют столько же элементов, сколько имеет множество натуральных чисел, называют счетными. Иными словами, множество называется счетным, если оно бесконечно, но его элементы можно перенумеровать натуральными номерами. Например, множество четных чисел, множество нечетных чисел, множество простых чисел, да и вообще любая бесконечная часть множества натуральных чисел являются счетными множествами.

Иногда, для того чтобы установить счетиость того или иного множества, надо проявить изобретательность. Возьмем, например, множество всех целых чисел (как положительных, так и отрицательных):

Если мы попробуем нумеровать его по порядку, начиная с какого-нибудь места, то никогда эту нумерацию не закончим. Поэтому все числа до выбранного места останутся незанумерованными. Чтобы не пропустить при нумерации ни одного числа, надо записать это множество в виде двух строк

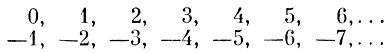
и нумеровать по столбцам. При этом 0 получит № 1, -1 - № 2, 1 - № 3, -2 - № 4 и т. д. Иными словами, все положительные числа и нуль нумеруются нечетными числами, а все отрицательные целые числа - четными. Это похоже на то, как директор гостиницы поместил всех филателистов в гостиницу, заполненную космозоологами.

Но если в то, что множество всех целых чисел счетно, легко поверить, то в счетность множества рациональных чисел поверить труднее. Ведь рациональные числа расположены очень густо - между любыми двумя рациональными числами найдется еще бесконечно много рациональных чисел. Поэтому совершенно непонятно, как их нумеровать; кажется, что между любыми двумя числами надо перенумеровать еще бесконечно много чисел и этот процесс никогда не закончится. И действительно, занумеровать рациональные числа в порядке возрастания их величины невозможно.

Однако если отказаться от расположения рациональных чисел в порядке возрастания, то занумеровать их все же удается. Сделаем так: выпишем сначала все положительные дроби со знаменателем 1, потом все положительные дроби со знаменателем 2, потом со знаменателем 3 и т. д. У нас получится таблица следующего вида:

Ясно, что в этой таблице мы встретим любое положительное рациональное число, и притом не один раз. Например, число 3 встретится и в виде дроби ³/₁, и в виде дроби ⁶/₂, и в виде дроби ⁹/₃.

Теперь приступим к нумерации. Для этого вспомним последний подвиг директора необыкновенной гостиницы, который расселил в ней жителей из бесконечного множества таких же гостиниц. Он тогда воспользовался нумерацией по квадратам. Точно так же поступим и мы, только с тем осложнением, что некоторые дроби будем пропускать (например, так как ¹/₁ получила уже № 1, то дроби ²/₂, ³/₃ и т. д. пропустим: они выражают то же самое число). Получится следующая нумерация положительных рациональных чисел: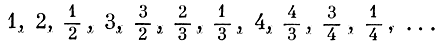

Мы занумеровали, таким образом, все положительные рациональные числа. А теперь уже легко понять, как нумеруются все (то есть положительные и отрицательные) рациональные числа. Для этого надо записать их отдельно в виде двух таблиц и числа одной таблицы нумеровать четными номерами, а второй - нечетными (и еще оставить один номер для нуля).

Вообще, складывая счетное множество счетных множеств, мы снова получим счетное множество. Это доказывается тем же самым приемом нумерации по квадратам.

Алгебраические числа. Нам удалось занумеровать все рациональные числа. Но рациональные числа получаются из натуральных чисел с помощью лишь одной операции - деления (и еще, быть может, изменения знака). А теперь мы добавим еще операцию извлечения корня и будем рассматривать все числа, которые можно получить из натуральных чисел с помощью этой операции и арифметических действий. Среди этих чисел будут такие, как 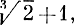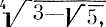и даже такие "монстры", как

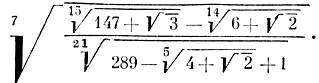
Возникает вопрос: можно ли занумеровать множество всех таких чисел? Это кажется еще более трудным, чем занумеровать множество рациональных чисел. В самом деле, какому числу надо приписать меньший номер: 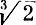или 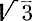? Но оказывается, что и это множество счетно, то есть его элементы можно перенумеровать.

Чтобы доказать это утверждение, отметим сначала, что каждое число рассматриваемого вида является корнем алгебраического уравнения вида

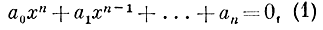
где a₀≠0 и a₀ , ..., a_n - целые числа. Например, ³/₇ - корень уравнения 7x - 3 = 0, 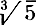- корень уравнения x³ - 5 = 0, а 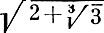- корень уравнения x⁶ - 6x⁴ + 12x² - 11 = 0. Иногда бывает очень трудно написать уравнение, которому удовлетворяло бы число описанного выше вида, но тем не менее это всегда возможно.

Заметим, что далеко не все корни уравнений вида (1), где a₀,..., a_n - целые числа, выражаются через натуральные числа с помощью арифметических действий и операции извлечения корня. Например, корни уравнения

нельзя выразить в таком виде, оно, как говорят, не решается в радикалах. Все числа, являющиеся корнями уравнений вида (1) с целыми коэффициентами, называют алгебраическими числами. Таким образом, множество алгебраических чисел содержит в себе множество всех чисел, выражаемых через натуральные с помощью арифметических действий и извлечений корней. Поэтому если нам удастся перенумеровать все алгебраические числа, то тем более мы решим задачу, поставленную в начале этого пункта.

Но прежде чем нумеровать алгебраические числа, надо перенумеровать сами алгебраические уравнения вида (1), А тогда задача будет уже решена. Ведь каждое алгебраическое уравнение n-й степени имеет не более n корней. Поэтому после того, как все уравнения с целыми коэффициентами будут перенумерованы, мы составим таблицу, в первой строке которой будут все различные корни первого уравнения, во второй - все различные корни второго уравнения, не попавшие в первую строку, в третьей- все различные корни третьего уравнения, не попавшие в первую или вторую строку, и т. д. Таблица получится такая:

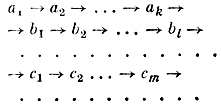
Теперь ясно, как нумеруются все числа этой таблицы (порядок нумерации указан стрелками).

Итак, займемся нумерацией множества алгебраических уравнений с целыми коэффициентами. Для этого применим идею, с помощью которой пробовал решить самую трудную задачу директор гостиницы. Напомним, что он предложил воспользоваться числами вида 2^m3ⁿ. Чтобы решить нашу задачу, придется использовать все простые числа. Читатель, конечно, помнит, что любое натуральное число единственным образом представляется в виде произведения простых множителей.

Поступим следующим образом. Сначала перенумеруем все целые числа (это мы уже умеем делать). Номер целого числа a обозначим через a. Каждому уравнению вида a₀xⁿ + a₁x^n-1 + ... + a_n = 0 (где, напомним, a₀,..., a_n - целые числа) поставим в соответствие число

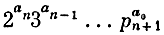
(через p_n+1 здесь обозначено (n-+1)-е простое число). Например, уравнению 3x² - 2 = 0 ставим в соответствие номер 2⁴3¹5⁶ = 150 000, потому что целое число -2 имеет номер 4, нуль - номер 1, а целое число 3 - номер 5. Теперь каждое уравнение получило свой номер, причем разным уравнениям соответствуют разные номера (каждый номер N единственным образом разлагается на простые множители, то есть единственным образом задает числа a_n, a_n+1,..., a₀; этим же числам соответствуют определенные целые числа a_n, a_n-1, ..., a₀, а тем самым и определенное уравнение a₀xⁿ+ ... + a_n = 0).

Неравные множества. Мы уже выяснили, что значат слова "два множества имеют поровну элементов".

А теперь выясним, что значит "одно множество имеет больше элементов, чем второе". Для конечных множеств это тоже можно выяснить, не прибегая к счету. Вспомним пример с танцплощадкой.

Если после того, как заиграет оркестр и юноши пригласят девушек танцевать, некоторые нерасторопные юноши окажутся не у дел, то ясно, что юношей больше. Если же часть девушек будет с грустью наблюдать за своими танцующими подругами, то ясно, что больше девушек.

В этих случаях мы поступали так: устанавливали взаимно однозначное соответствие между одним множеством и частью другого множества. Если это удавалось, то отсюда следовало, что второе множество содержит больше элементов, чем первое. Пользуясь этим методом, легко установить, например, что рыб в океане меньше, чем атомов на земном шаре (хотя оба эти множества и конечны, их вряд ли возможно пересчитать). Для этого достаточно каждой рыбе поставить в соответствие один атом, входящий в состав ее тела. Тем самым будет установлено взаимно однозначное соответствие между множеством всех рыб и частью множества всех атомов на земном шаре.

К сожалению, для бесконечных множеств так просто поступить нельзя. Ведь мы уже видели, что множество может иметь столько же элементов, сколько и его часть. Поэтому только из того, что множество A имеет столько же элементов, сколько часть множества B, еще нельзя заключить, что оно имеет меньше элементов, чем все множество B.

Мы скажем, что если A можно поставить во взаимно однозначное соответствие с частью множества B, то множество B имеет не меньше элементов, чем множество A. Можно доказать, что это отношение обладает всеми свойствами неравенств:

1. каждое множество имеет не меньше элементов, чем оно само;
2. если в одном множестве не меньше элементов, чем во втором, а во втором - не меньше элементов, чем в третьем, то первое множество имеет не меньше элементов, чем третье;
3. если каждое из двух множеств имеет не меньше элементов, чем другое, то оба имеют поровну элементов (то есть между элементами этих множеств можно установить взаимно однозначное соответствие).

Первое свойство вытекает из того, что, ставя в соответствие каждому элементу множества A сам этот элемент, получаем взаимно однозначное отображение A на себя. Прозрачен и смысл второго свойства: если A можно взаимно однозначно отобразить на часть множества B, а B - на часть множества C, то существует взаимно однозначное отображение A на часть C.

А вот третье свойство при всей простоте его формулировки означает довольно сложное утверждение: если можно взаимно однозначно отобразить множество A на часть множества B, а множество B на часть множества A, то существует и взаимно однозначное отображение всего множества A на B. То, что дело обстоит таким образом, с самого начала подозревал Г. Кантор. Однако ему в течение долгого времени не удавалось найти доказательства этого утверждения. О своих затруднениях он рассказал в 1897 г. на лекциях по теории множеств для студентов университета в Галле. Через несколько дней один из слушателей, 19-летний Феликс Бернштейн^*, принес Кантору доказательство этого утверждения, основанное на той же идее, с помощью которой директор космической гостиницы помещал в нее новых постояльцев. Поэтому сейчас это утверждение называют теоремой Кантора-Бернштейна. Лишь через много лет в оставшихся после смерти немецкого математика Дедекинда бумагах нашли полученное им еще в 1887 г. доказательство той же теоремы.

^* (Бернштейн Феликс (1878-1956) - немецкий математик.)

Выясним теперь, в каких же случаях говорят, что мощность множества A меньше мощности множества B. Может случиться, что множество B имеет не меньше элементов, чем множество A, но эти множества не эквивалентны. Иными словами, может случиться, что есть взаимно однозначное соответствие между множеством A и частью B₁ множества B, но не существует взаимно однозначного соответствия между A и всем множеством B. Вот в этом случае мы и будем говорить, что A имеет меньше элементов, чем B.

Счетное множество - самое маленькое из бесконечных. Мы уже говорили, что любая бесконечная часть множества натуральных чисел счетна. Это означает, что не может существовать бесконечное множество, мощность которого была бы меньше мощности счетного множества. Докажем теперь, что в каждом бесконечном множестве есть счетное подмножество. Отсюда будет следовать, что мощность счетного множества не больше мощности любого бесконечного множества, то есть что эта мощность - самая маленькая из бесконечных.

Чтобы выбрать счетное подмножество из бесконечного множества A, поступим так. Выберем один элемент x₁ - это можно сделать, так как множество A бесконечно и, во всяком случае, не пусто. Ясно, что после удаления элемента x₁ множество A не исчерпывается, и мы сможем выбрать из него второй элемент x₂. После этого выберем третий элемент x₃ и т. д. В результате мы извлечем из множества А счетное подмножество занумерованных элементов

Немного усовершенствовав это доказательство, можно добиться, чтобы после удаления счетного подмножества осталось бесконечное множество. Для этого надо после извлечения подмножества X вернуть обратно все элементы с четными номерами. В результате получится, что мы извлекли счетное подмножество

а оставшееся множество еще содержит бесконечное множество элементов {x₂, x₄, x₆, ..., x_2n, ...} и, быть может, еще много других элементов.

Нетрудно доказать следующие теоремы.

Мощность бесконечного множества не изменяется от прибавления к нему счетного множества.

Мощность несчетного множества не меняется от удаления из него счетного множества.

Эти теоремы еще раз подтверждают, что счетные множества - самые малые из бесконечных множеств.

Несчетные множества. Все построенные до сих пор множества оказались счетными. Это наводит на мысль: а не являются ли вообще все бесконечные множества счетными? Если бы это оказалось так, то жизнь математиков была бы легкой: все бесконечные множества имели бы поровну элементов и не понадобился бы никакой анализ бесконечности. Но выяснилось, что дело обстоит куда сложнее: несчетные множества существуют и притом могут иметь самые разные мощности. Одно несчетное множество всем хорошо знакомо - это множество всех точек на прямой линии. Но прежде чем говорить об этом множестве, мы расскажем о другом, тесно связанном с ним множестве A вариантов заполнения необыкновенной гостиницы.

Заметим, что доказать несчетность какого-то множества вообще нелегко. Ведь доказать, что какое-то множество счетно, это значит просто придумать правило, по которому нумеруются его элементы. А доказать несчетность какого-то множества, это значит доказать, что такого правила нет и быть не может. Иными словами, какое бы правило мы ни придумали, всегда найдется незанумерованный элемент множества. Чтобы доказывать несчетность множеств, Кантор придумал очень остроумный способ, получивший название диагонального процесса. Метод доказательства Кантора станет ясен из следующего рассказа Иона Тихого.

Несостоявшаяся перепись. До сих пор я рассказывал об удачах директора необыкновенной гостиницы: о том, как ему удалось вселить в заполненную гостиницу еще бесконечно много постояльцев, а потом даже жителей из бесконечного множества столь же необычных гостиниц. Но был случай, когда и этого мага и чародея постигла неудача.

Из треста космических гостиниц пришел приказ составить заранее все возможные варианты заполнения номеров. Эти варианты потребовали представить в виде таблицы, каждая строка которой изображала бы один из вариантов. При этом заполненные номера должны были изображаться единицами, а пустые нулями. Например, вариант

означал, что все нечетные номера заняты, а все четные пустые, вариант

означал заполнение всей гостиницы, а вариант

означал полный финансовый крах - все номера пустовали.

Директор был перегружен работой и поэтому придумал простой выход из положения. Каждой дежурной по этажу было поручено составить столько вариантов заполнения, сколько номеров было в ее ведении. При этом были приняты меры" чтобы варианты не повторялись. Через несколько дней списки были представлены директору, и он объединил их в один список.

- Уверены ли Вы, что этот список полон? - спросил я директора.- Не пропущен ли какой-нибудь вариант?

- Не знаю,- ответил он.- Вариантов в списке бесконечно много, и я не понимаю, как проверить, нет ли еще какого-нибудь варианта.

И тут у меня блеснула идея (впрочем, быть может, я несколько преувеличиваю свои способности, просто беседы с профессором Тарантогой о бесконечных множествах не прошли бесследно).

- Могу ручаться, что список неполон. Я берусь указать вариант, который наверняка пропущен.

- С тем, что список неполон, я еще соглашусь. А вот пропущенного варианта указать не удастся - ведь здесь уже бесконечно много вариантов.

Мы заключили пари. Чтобы выиграть его, я предложил прибить каждый вариант на дверь того номера, которому он соответствовал (если читатель помнит, вариантов было составлено именно столько, сколько было номеров в гостинице). А потом я поступил очень просто. Подойдя к двери первого номера, я увидел, что соответствующий вариант начинается с цифры 0. Немедленно в блокноте появилась цифра 1; это и была первая цифра варианта, который мне хотелось составить.

Когда я подошел к двери второго номера, то первая цифра соответствующего варианта меня не интересовала, ведь первая цифра моего варианта была уже написана. Поэтому все внимание было обращено на вторую цифру. Увидев, что эта цифра 1, я записал в своем блокноте цифру 0. Точно так же, обнаружив, что третья цифра варианта, прибитого к двери третьего номера, тоже 1, я записал в блокноте цифру 0. Вообще, если я обнаруживал, что n-я цифра n-го варианта есть 0, то писал в своем блокноте на n-м месте цифру 1, если же n-я цифра n-го варианта была 1, то n писал у себя 0.

Когда я обошел все номера гостиницы, то в блокноте оказалась записанной последовательность нулей и единиц.

Войдя в кабинет директора, я сказал:

- Вот, полюбуйтесь на пропущенный вариант.

- А откуда известно, что он пропущен?

- Он не может быть первым, так как отличается от него первой цифрой, не может быть вторым, так как отличается от него второй цифрой, третьим, так как отличается от него третьей цифрой, и вообще n-м, так как отличается от него n-й цифрой.

Пари было выиграно, и я получил вечное право бесплатного проживания в этой гостинице.

Но одновременно стало ясно, что какое бы счетное множество вариантов ни взять, всегда найдется вариант, не вошедший в это множество (эти варианты всегда можно развесить по дверям номеров). А это и значит, что множество всех вариантов заполнения гостиницы несчетно, задача, поставленная перед директором, оказалась невыполнимой.

Было решено дать об этом телеграмму. Надо сказать, что и телеграф в необыкновенной гостинице был тоже необычным, он передавал телеграммы, состоящие не из конечного, а из бесконечного (точнее говоря, счетного) множества точек и тире. Например, они имели такой вид:

Я сразу сообразил, что и множество таких телеграмм тоже несчетно, ведь вместо точек и тире можно ставить нули и единицы, а тогда не будет никакой разницы между телеграммами со счетным множеством знаков и множеством всех вариантов заполнения гостиницы.

Отправив телеграмму, я тепло попрощался с директором гостиницы и полетел в галактику РГЦ-8067, где должен был произвести астрографическую съемку...

Несчетность континуума. Теперь уже несложно доказать, что множество всех точек на прямой линии несчетно. Вместо этого множества можно говорить о множестве всех действительных чисел, так как каждой точке прямой соответствует действительное число и обратно.

Каждое действительное число можно записать в виде бесконечной десятичной дроби вида

Некоторые из них имеют даже по две записи; например, 0,500000... и 0,49999999... - это одно и то же число. Для определенности будем пользоваться записью с нулями.

Предположим, что нам удалось каким-то образом перенумеровать все действительные числа. Чтобы доказать, что это предположение неверно, достаточно построить хоть одно незанумерованное число. Следуя примеру Иона Тихого, поступим следующим образом.

Сначала напишем нуль и поставим после него запятую. Потом возьмем число, получившее первый номер, и посмотрим на его первый десятичный знак после запятой (то есть на число десятых). Если эта цифра отлична от 1, то в числе, которое мы пишем, поставим после запятой 1, а если эта цифра равна 1, то поставим после запятой 2. Затем перейдем к числу, получившему второй номер, и посмотрим на его вторую цифру после запятой. Снова если эта цифра отлична от единицы, то в числе, которое мы пишем, поставим на месте сотых цифру 1, если же эта цифра является единицей, то поставим цифру 2. Точно так же будем действовать и дальше, каждый раз обращая внимание лишь на n-ю цифру числа, получившего n-й номер. В результате мы выпишем некоторое число, например

Ясно, что это число не получило никакого номера: в первом десятичном знаке оно отличается от числа с номером 1, во втором - от числа с номером 2, ..., в n-м - от числа с номером n и т. д.

Чтобы читателю стало яснее, как выписывается число, не получившее номера, предположим, что при выбранной нумерации первые пять чисел имеют следующий вид:

Тогда число, не получившее номера, будет начинаться со следующих десятичных знаков:

Разумеется, не только это, но и многие другие числа не получили номеров (мы могли бы заменять все цифры, кроме 2, на 2, а цифру 2 на 7 или выбрать еще какое-нибудь правило). Но нам достаточно существования одного-единственного числа, не получившего номера, чтобы опровергнуть гипотезу о возможности нумерации всех действительных чисел.

Существование трансцендентных чисел. Мы говорили, что алгебраическими числами называют числа, являющиеся корнями уравнений

с целыми коэффициентами. Числа же, не являющиеся корнями таких уравнений, называют трансцендентными.

В течение долгого времени математики имели дело лишь с алгебраическими числами, такими, как 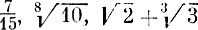и т. д. Лишь ценой больших усилий французскому математику Лиувиллю^* удалось найти в 1844 г. несколько трансцендентных чисел. А доказательство трансцендентности числа π, проведенное Линдеманом^** в 1882 г. было большим научным событием: ведь из него следовала невозможность квадратуры круга.

^* (Лиувилль Жозеф (1809-1882) - французский математик, автор работ по математическому анализу и теории чисел.)

^** (Линдеман Карл (1852-1939) - немецкий математик, доказал трансцендентность числа π.)

И вдруг оказалось, что алгебраические числа, которые встречаются на каждом шагу, на самом деле являются величайшей редкостью, а трансцендентные числа, которые так трудно строить,- обычным правилом. В самом деле, мы уже видели, что алгебраические числа образуют лишь счетное множество. Множество же всех действительных чисел, как мы только что обнаружили, несчетное. Значит, несчетна и разность множества действительных чисел и множества алгебраических чисел, а это и значит, что множество трансцендентных чисел несчетно.

Это доказательство существования трансцендентных чисел, полученное Кантором в 1873 г., отличалось от доказательства Лиувилля тем, что опиралось лишь на общие соображения о счетности и несчетности множеств, а не на специальные свойства алгебраических чисел. Из теорем Лиувилля вытекает, например, что число 0,1010010000001..., в десятичной записи которого после n-й единицы стоит n! нулей, трансцендентно. А для того чтобы получить пример трансцендентного числа исходя из доказательства Кантора, придется пройти гораздо более длинный путь: сначала занумеровать все алгебраические числа, потом записать их в виде десятичных дробей и, наконец, строить диагональным процессом искомое число. Вряд ли за обозримый промежуток времени удастся ответить, чему равен, например, десятичный знак этого числа с номером 10¹⁰⁰. А метод Лиувилля позволяет строить трансцендентные числа, для которых, хотя и с трудом, ответить на такие вопросы можно. Таким образом, общность метода доказательства оборачивается его слабостью при переходе к конкретным вопросам.

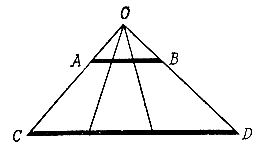
Рис. 8

На длинном и коротком отрезках поровну точек. До тех пор пока читатель не познакомился с удивительными свойствами бесконечных множеств, ответ на вопрос: "Где больше точек, на отрезке длиной в 1 мм или на отрезке длиной в 1 м?" - вряд ли вызвал бы у него хоть тень сомнения. Ясно, что на отрезке в 1 м куда больше точек, он ведь в 1000 раз длиннее. Но теперь, вероятно, читатель поостережется делать столь безапелляционные заявления - уж слишком непохожи свойства бесконечных множеств на то, чему учит обыденная жизнь. И действительно, на очень коротком и очень длинном отрезках точек поровну! Иными словами, всегда можно установить взаимно однозначное соответствие между точками этих отрезков. Как это сделать, лучше всего видно из рис. 8. Центральная проекция из точки O ставит в соответствие точке A точку C, точке B - точку Д и т. д. В результате каждой точке отрезка АВ соответствует одна и только одна точка отрезка CD.

Трудно примириться с мыслью, что дорога длиной в миллион световых лет имеет столько же точек, сколько и радиус атомного ядра!

Но еще неожиданнее оказалось то, что даже на всей бесконечной прямой не больше точек, чем на отрезке, то есть что между множеством точек на прямой и множеством точек на отрезке можно установить взаимно однозначное соответствие.

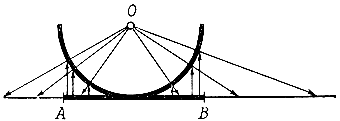
Рис. 9

Мы возьмем даже не весь отрезок, а выбросим из него концы (как говорят, возьмем не отрезок, а промежуток). Как установить взаимно однозначное соответствие между промежутком и прямой, видно из рис. 9. Сначала точки промежутка отображают на полуокружность, а потом проектируют полуокружность на прямую. Ясно, что при этом каждой точке промежутка соответствует одна и только одна точка прямой, причем ни одна точка на прямой не пропущена.

Впрочем, это соответствие можно установить и по другому, с помощью кривой - тангенсоиды, графика функции y = tg x (рис. 10).

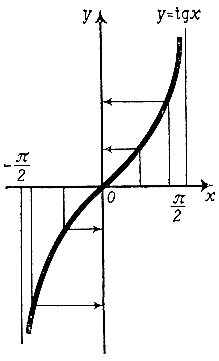
Рис. 10

Отрезок и квадрат. С тем, что на бесконечной прямой столько же точек, сколько и на отрезке, математики, скрепя сердце, примирились. Но следующий результат Кантора оказался еще более неожиданным. В поисках множества, имеющего больше элементов, чем отрезок, он обратился к множеству точек квадрата. Сомнения в результате не было: ведь отрезок целиком размещается на одной стороне квадрата, а множество всех отрезков, на которые можно разложить квадрат, само имеет ту же мощность, что и множество точек отрезка.

На протяжении трех лет (с 1871 по 1874 г.) Кантор искал доказательство того, что взаимно однозначное соответствие между точками отрезка и точками квадрата невозможно.

Шли годы, а желанный результат не получался. И вдруг совершенно неожиданно ему удалось построить соответствие, которое он считал невозможным! Сначала он сам не поверил себе. Своему другу и единомышленнику Дедекинду он писал: "Я вижу это, но не верю".

Но все же пришлось смириться с тем, что интуиция подвела и здесь - в квадрате оказалось ровно столько же точек, сколько и на отрезке. Строгое доказательство этого утверждения несколько осложняется из-за неоднозначности десятичной записи чисел. Поэтому мы дадим лишь эскиз доказательства Кантора.

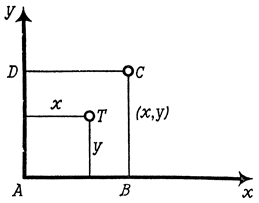
Рис. 11

Возьмем отрезок [0, 1] и квадрат со стороной 1. Этот квадрат можно считать расположенным так, как на рис. 11. Нам надо установить взаимно однозначное соответствие между точками отрезка и квадрата. Проектирование точек квадрата на отрезок АВ здесь не помогает, ведь при проектировании в одну точку отрезка перейдет бесконечное множество точек квадрата (например, в точку А - все точки отрезка DA).

Решение получается следующим образом. Каждую точку T квадрата ABCD можно задать двумя числами - ее координатами x и y (или попросту ее расстояниями до сторон АВ и AD). Эти числа можно записать как бесконечные десятичные дроби. Так как x и y не больше 1, то эти дроби имеют вид

(для простоты мы не берем точки квадрата, лежащие на его сторонах, а берем лишь внутренние точки). Здесь α_n и β_n - десятичные знаки чисел x и y, например, если x = 0,63205... и y = 0,21357..., то α₁ = 6, α₂ = 3, α₃ = 2 и т. д., а β₁ = 2, β₂ = 1, β₃ = 3 и т. д.

Нам надо теперь найти точку Q отрезка АВ, соответствующего точке Т. Достаточно указать длину отрезка AQ. Мы выберем эту длину равной числу z, десятичные знаки которого получаются путем "перетасовывания" десятичных знаков чисел хну. Иными словами, сделаем из двух записей (1) и (2) третью, написав их десятичные знаки через один:

Например, если

и

то

Точка z лежит на отрезке [0, 1], и ясно, что различным точкам квадрата соответствуют при этом разные точки отрезка. Ведь если точки T и T' не совпадают, то в десятичных записях чисел x и x' или y и y' хоть один знак будет разный. Но это приведет к тому, что десятичные записи соответствующих чисел z и z' не совпадут. Несколько более подробный анализ показывает, что тогда не совпадают и сами эти точки.

Всех точек отрезка мы не получим. Например, точка z = 0,191919... должна была бы получиться из пары x = 0,111..., y = 0,999..., соответствующей точке на стороне квадрата, а такие точки мы условились не брать. Поэтому при отображении квадрата на отрезок точка z не будет образом ни одной точки квадрата.

Мы установили взаимно однозначное соответствие между точками квадрата и частью точек отрезка [0, 1]. Это показывает, что множество точек квадрата имеет не большую мощность, чем множество точек отрезка. Но его мощность и не меньше, а потому эти мощности совпадают.

Не только квадрат, но и куб имеет столько же точек, сколь и отрезок. Вообще любая геометрическая фигура, содержащая хоть одну линию, имеет столько же точек, сколько и отрезок. Такие множества называют множествами мощности континуума (от латинского continuum - непрерывный).

Существует ли множество самой большой мощности? Пока что самой большой мощностью, которую мы знаем, является мощность множества точек на прямой, то есть мощность континуума. Ни множество точек квадрата, ни множество точек куба не имеют большей мощности. Не является ли мощность континуума самой большой? Оказывается, что нет. Более того, вообще нет множества самой большой мощности. Для любого множества A есть множество, мощность которого больше мощности A. Этим множеством является, например, множество В всех функций, заданных на множестве A и принимающих значения 0 и 1.

Покажем сначала, что мощность множества B не меньше, чем мощность множества A. Для этого каждой точке α множества A поставим в соответствие функцию f^a(x), принимающую в этой точке значение 1, а в остальных точках значение 0. Ясно, что разным точкам соответствуют разные функции. Например, если множество A состоит из трех точек 1, 2, 3, то точке 1 соответствует функция, принимающая в этой точке значение 1, а точке 2 - функция, принимающая в точке 1 значение 0. Эти функции не равны друг другу.

Итак, мощность множества B не меньше мощности множества A. Покажем теперь, что эти мощности не равны друг другу, то есть что нет взаимно однозначного соответствия между элементами множеств A и B.

В самом деле, предположим, что такое соответствие существует. Обозначим тогда функцию, соответствующую элементу a из A, через f_a(x). Напомним, что все функции f_a(x) принимают только два значения: 0 и 1.

Составим новую функцию φ(x), заданную равенством

Таким образом, чтобы найти значение функции φ(x) в некоторой точке а из A, надо найти сначала соответствующую этой точке функцию f_a(x) и вычесть из 1 значение этой функции x = a. Ясно, что функция φ (x) также задана на множестве A и принимает значения 0 и 1. Следовательно, φ (x) является элементом множества B. Но тогда, по предположению, φ (x) соответствует некоторой точке b из A, а значит,

Учитывая первое равенство для φ(x), получаем, что для всех x из A

Положим в этом равенстве x = b. Мы найдем тогда, что

и потому

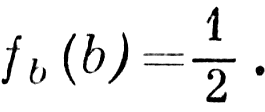
Но это противоречит тому, что значения функции f_b(x) равны 0 и 1. Полученное противоречие показывает, что взаимно однозначного соответствия между множествами A и B быть не может.

Итак, для любого множества A можно построить множество B большей мощности. Поэтому множества самой большой мощности не существует. Отправляясь от самой малой из бесконечных мощностей - мощности множества натуральных чисел, мы получим сначала мощность континуума, потом мощность множества всех функций, заданных на множестве действительных чисел, и будем без конца подниматься вверх по этой головокружительной лестнице все увеличивающихся бесконечных мощностей.

Арифметика бесконечности. Арифметика натуральных чисел не сводится к простому счету "один, два, три..." Натуральные числа можно складывать и вычитать, умножать и возводить в степень. Эти операции тесно связаны с операциями над конечными множествами. Складывая натуральные числа m и n, мы подсчитываем число элементов в объединении двух множеств, одно из которых содержит m элементов, а другое - n элементов (при этом, конечно, нужно, чтобы объединяемые множества не имели общих элементов - иначе получится меньше элементов, чем нужно). А умножая m на n, мы подсчитываем число пар (a, b), первый элемент которых принадлежит множеству A, состоящему из m элементов, а второй - множеству B, содержащему n элементов. В математике множество таких пар называют декартовым произведением множеств A и B и обозначают A×B.

Обозначим объединение множеств A и B, не имеющих общих элементов, через A+B, а мощность множества A - через |A|. Тогда сказанное выше можно записать так:

Но левые части этих равенств имеют смысл и для бесконечных множеств. Это позволяет определить операции сложения и умножения для бесконечных мощностей. С их помощью установленные ранее утверждения о мощностях можно записать в виде формул, где через N обозначено множество натуральных чисел, а через Δ - множество точек отрезка [0; 1]:

и т. д. Например, равенство |N||N| = |N| означает, что счетное множество счетных множеств счетно, а равенство |Δ||Δ| = |Δ|,- что квадрат имеет столько же точек, что и отрезок.

Для бесконечных мощностей можно определить и операцию возведения в степень с бесконечным же показателем. Несложно доказать, что число отображений множества A в множество B равно |B|^|A|. Поэтому и для бесконечных мощностей смысл записи |B|^|A| определяется аналогичным образом. Например, равенство 2^|N| = |Δ| означает, что множество бесконечных последовательностей, составленных из нулей и единиц, имеет мощность континуума.

Далеко не все законы обычной арифметики переносятся в область арифметики натуральных чисел. Кантор говорил, что законы арифметики бесконечности коренным образом отличаются от зависимостей, царящих в области конечного.

Трансфинитные числа. Натуральные числа применяют не только для ответа на вопрос "сколько?", но и для ответа на вопрос "какой по счету?" Иными словами, их используют не только как количественные, но и как порядковые числа. Мощности можно использовать лишь как количественные числа. Для описания порядка нужны иные понятия. Даже самое простое из бесконечных множеств - множество N натуральных чисел - можно упорядочить бесчисленной совокупностью возможностей. Кроме стандартного расположения 1, 2, 3, 4, 5, 6, ... можно поступить и так: сначала взять все нечетные числа (с их обычным порядком), а потом все четные: 1, 3, 5, ..., 2, 4, 6, ... Но при попытке перенумеровать числа в таком порядке нас постигнет неудача - все номера окажутся затраченными на нечетные числа, а на долю четных чисел ничего не останется. Поэтому кроме обычных номеров понадобятся символы новой природы. Кантор предложил при таком порядке расположения чисел нумеровать число 2 символом ω, число 4 - символ ω+1 и т. д.

Еще больше символов понадобится, если сначала выписать все числа, делящиеся на 3, потом дающие при делении на 3 остаток 1, и, наконец, числа, дающие при таком делении остаток 2:3,6, 9,..., 1,4,7,..., 2,5,8,... Здесь для нумерации числа 2 понадобится символ ω*2, число 5 будет занумеровано символом ω*2+1 и т. д. А если выписать сначала все простые числа, потом числа, разлагающиеся в произведение двух простых множителей, трех простых множителей и т. д., а в самом конце записать число 1, которое не относится ни к простым, ни к составным числам, то для обозначения последнего элемента придется применить совсем новый символ ω^ω.

Кантор придумал еще много различных расположений множества натуральных чисел, причем все они (как и разобранные выше) обладали следующим свойством: каждая часть множества натуральных чисел имела в таком расположении наименьший элемент. Он назвал множества, элементы которых расположены в одном из этих порядков, вполне упорядоченными (термин применяется и для несчетных множеств), а символы, введенные им для нумерации элементов вполне упорядоченных множеств,- трансфинитными числами (от латинских слов trans - за и finitae - конечный). Изучая свойства трансфинитных чисел, Кантор пришел к следующей проблеме: какую мощность имеет множество всех счетных трансфинитов? Легко показать, что она несчетна, но не превосходит мощности континуума. А вот равна ли она этой мощности или меньше ее, на этот вопрос не смогли дать ответ ни сам Кантор, ни его многочисленные ученики и последователи. О современном состоянии указанной проблемы, называемой проблемой континуума, будет рассказано в главе 4.

В начале XX в. теория бесконечных множеств превратилась в модную область математической науки. Некоторые специалисты придавали очень большое значение исследованиям в этой области. Например, А. Френкель писал: "Завоевание актуальной бесконечности методами теории множеств можно рассматривать как расширение нашего научного кругозора, не меньшее по значению, чем коперникова система в астрономии и теория относительности и даже квантовая теория в физике".

Но самый строгий судья научных теорий - время ставит в конце концов все на свои места. Постепенно все реже и реже стали появляться работы, в которых бы использовались трансфинитные числа, исследовались мощности, отличные от счетной или континуальной. Множества с такими мощностями можно получить, рассматривая, например, все части плоскости или все функции на отрезке [0; 1]. Но дело в том, что и в теоретических исследованиях, и для решения практических проблем, нужны не любые части плоскости и не любые функции, а лишь получаемые с помощью фиксированных процессов из некоторых простейших. А множества таких "хороших" частей или функций имеют мощность континуума.

И хотя, по словам П. С. Александрова^* и А. Н. Колмогорова^**, "огромное влияние теории множеств на развитие математики последнего полустолетия является в настоящее время общепризнанным факушм", в настоящее время это влияние идет совсем по иным каналам. В следующей главе мы расскажем о том, как изменилось лицо некоторых областей математики под влиянием теоретико-множественных концепций.

^* (Александров Павел Сергеевич (1896-1982) - советский математик, создатель советской топологической школы.)

^** (Колмогоров Андрей Николаевич (р. 1903) - советский математик, автор ряда замечательных работ в области теории функций действительного переменного, теории вероятностей, топологии.)