Глава 1. Бесконечность и Вселенная

От мифологии к науке. Изучение сделанных из камня изображений и нанесенных охрой и углем рисунков на стенах пещер убедительно показывает, что уже десятки тысяч лет тому назад люди не только накапливали сведения о поведении животных и птиц, свойствах трав и плодов, но и пытались установить закономерности окружающего их мира, понять его происхождение. Так складывались древнейшие мифы о "Великой праматери" - общем предке людей и животных, о тотемах - покровителях племени, а влиянию потусторонних сил приписывал древний человек такие грозные явления природы, как гром и молния, землетрясения и ураганы.

По мере развития земледелия и животноводства возрастала роль наблюдений за небом: положение небесных светил подсказывало, когда надо начинать сеять или убирать урожай, с неба шел дождь, орошавший поля и пастбища, с неба же опускалась на посевы и сады саранча - один из самых опасных врагов древнего земледельца. Поэтому древняя мифология охватывала не только Землю, но и небо.

Неудивительно поэтому, что люди стали обожествлять силы природы и помещать жилище богов на небесах. Так возникли первые мифы о происхождении мира, о взаимосвязи явлений природы. Почти во всех этих мифах первоначальное состояние мира описывалось либо как хаос, либо как океан. А потом происходило разделение неба и земли, воды и суши. Например, в аккадских мифах рассказывается, как бог Мардук победил богиню Тиамат, символизировавшую первоначальный океан, и сотворил небо и землю из ее гигантского тела, разрубив его надвое.

Более символизированный вид имели мифы древней Индии, созданные арийскими племенами, вторгшимися в Индостан где-то между 1500 и 1200 годами до н. э. В них рассказывается о борьбе данавов и адитьев, что можно примерно перевести как стесненность и неограниченность, или, иначе, как ограниченное и беспредельное. Победу адитьев обеспечил бог Индра, который, по-видимому, считался сыном Неба и Земли. Когда он чудесным образом вырос до устрашающих размеров, Небо и Земля, испугавшись, разлетелись в разные стороны.

Похожие мифы существовали и у древних иранцев, культура которых в далеком прошлом составляла одно целое с культурой ариев. По их рассказам бог Ормазд сперва создал из сверкающего металла светлое и ясное небо в форме яйца. Вершиной оно достигало до Бесконечного Света, а все творение было создано внутри неба. Землю иранцы считали круглой и висящей в середине неба, как желток находится в середине яйца.

В мифологии древних греков мир распадался на три области - подземное царство, землю и небо, окруженные со всех сторон океаном (это объясняло, почему вода и бьет вверх из источников и падает на землю дождем).

Мифы позволяли людям устанавливать ассоциации между далекими понятиями, осмысливать каким-то образом окружающий их мир. При этом действие в мифах происходило вне времени и пространства и вне ограничений, налагаемых логикой. И поскольку миф отражал опыт предшествующих поколений, его нельзя было опровергнуть тем, что он противоречит опыту отдельной личности.

Но по мере развития производства и усложнения общественных отношений происходил извечный процесс развития понятийного аппарата, появилась возможность проверять непротиворечивость умозаключений с помощью логики, минуя мифологию. Миф начал вступать в противоречие с разумом, с логическими понятиями, сфера мифотворчества стала сужаться, появились первые зачатки науки.

Традиция возводит начало научного осмысления мира к греческому философу Фалесу^*, которому удалось в 585 г. до и. э. предсказать солнечное затмение. Разумеется, это было невозможно, пока Солнце и Луну считали очами Неба или богами Гелиосом и Селеной.

^* (Фалес Милетский (ок. 625-547 до н. э.) - древнегреческий математик и астроном. Впервые ввел в математику понятие доказательства и доказал некоторые простейшие геометрические теоремы.)

Анаксимандр^*, опираясь на индоиранские учения о борьбе ограниченного с беспредельным, создал учение о том, что вся Вселенная произошла из беспредельного - апейрона. По Анаксимандру, апейрон неисчерпаем, бесконечен и вечен. Он учил, что существуют бесчисленные миры, обособленные друг от друга, причем, по его мнению, в каждом периоде мирообразования они возникают и уничтожаются.

^* (Анаксимандр Милетский (ок. 585-525 до н. э.) - древнегреческий философ, ученик Фалеса. Впервые высказал догадку о бесконечности миров и Вселенной.)

Многое в учениях Фалеса, Анаксимандра и их учеников кажется сейчас наивным (например, предположение Фалеса о том, что люди произошли от рыб.) Но были и гениальные догадки - у них можно найти мысли о шарообразности Земли, об эволюции живых существ и многое другое.

Самое же главное для темы нашей книги то, что в учениях этих философов началось обсуждение понятия беспредельности, бесконечности, выяснение вопроса о конечности или бесконечности Вселенной. Чтобы пояснить идею безграничности, Анаксимандр говорил: "Где бы ни стал воин, он сможет протянуть свое копье еще дальше". То же повторял потом живший в IV в. до н. э. видный математик пифагорейской школы Архит. Знаменитый атомист древности Демокрит считал, что Вселенная не только бесконечна, но и не имеет центра. Эти мысли в стихотворной форме изложил живший несколько столетий спустя римский поэт и философ Тит Лукреций Кар.

Нет и краев у нее, и нет ни конца, ни предела, 
И безразлично, в какой ты находишься части Вселенной: 
Где бы ты пи был, везде, с того места, что ты занимаешь, 
Все бесконечной она остается во всех направленьях.

А еще через несколько столетий великий среднеазиатский поэт Низами вопрошал:

Разве в мире бесконечном направлепье есть? 
Разве далям бесконечным измеренье есть?

Так возникшая на Востоке идея бесконечности пришла к греческим философам и ученым, была ими изучена и вновь вернулась на Восток. Известный немецкий математик Г. Вейль^* писал, что интуиция бесконечного, спокойное и не задающееся никакими вопросами признание ее были присущи восточному миру, но на Востоке эта интуиция оставалась лишь чисто абстрактным сознанием. Великим же достижением греческой пауки было, по мнению Вейля, преобразование полярной противоположности конечного и бесконечного в плодотворное оружие познания действительности.

^* (Вейль Герман (1885-1955) - немецкий математик, автор выдающихся работ по математическому анализу, дифференциальной геометрии, алгебре и теории чисел. Много занимался философией математики, является одним из создателей интуиционизма.)

Заметим, что на Востоке была создана и идея вечности Вселенной. В глубокой древности там была сложена следующая притча: "Вот алмазная гора высотой в тысячу локтей. Раз в столетие прилетает птичка и точит свой клюв о гору. Когда она сточит всю гору, пройдет первое мгновение вечности"^*.

^* (В других вариантах этой притчи гору стачивает фея Лилавати, которая раз в столетие, танцуя, касается ее концом своего шлейфа.)

Из древнегреческих философов ярко выразил идею вечности и изменяемости мира со временем Гераклит, учивший, что "все течет, и нельзя дважды войти в одну и ту же реку, ибо входящего будут омывать иные воды". Он говорил также: "Этот космос, один и тот же для всех, не создал никто ни из богов, ни из людей, но он всегда был, есть и будет вечно живым огнем, мерами вспыхивающим и мерами

угасающим".

Далеко ушла космология Гераклита от мифов древности! Ведь анализ древних мифов показывает, что когда-то пространство и время казались людям конечными, прерывными, состоящими из качественно различных кусков. В ту далекую эпоху идея развития мира была чужда человеческому разуму, а течение времени представлялось совершающимся по кругу с постоянным повторением времен года и положения планет и звезд (не случайно в древнегреческой мифологии бог времени Кронос был сыном бога неба Урана, а филологи находят, что слова время и вращение имеют общее происхождение). Даже когда стали представлять себе время текущим в одном направлении, они полагали, что мир имел начало (сотворение мира) и будет иметь конец (страшный суд в евангельских сказаниях, гибель богов в скандинавской мифологии и т. д.). Пространство же казалось ограниченным небесной твердью, где обитали боги. Понадобился поистине революционный переворот в человеческом сознании, чтобы возникло представление о мире, не имеющем границ, о мире без начала и без конца (впрочем, как мы увидим ниже, это представление оказалось слишком смелым даже для многих из лучших умов древнего мира).

"Как число песку на бреге морском". В древности философия, естествознание и математика были столь родственны, что ими, как правил о, занимались одни и те же люди. Например, Фалес не только философствовал о беспредельном и предсказывал затмения, но и первым начал доказывать геометрические теоремы, а создателем крупнейшей и влиятельнейшей философской школы в VI в. до н. э. был Пифагор, которому предание приписывает доказательство знаменитой теоремы о прямоугольном треугольнике.

Пифагор учил, что "все есть число", причем некоторые числа (1, 4, 7, 10) играли в его миропонимании особую роль. Впрочем, мнение о мистической роли числа 7 возникло еще у древних шумеров задолго до того, как в Греции начала развиваться математика. В их мифах можно встретить семь духов бурь, семь злых болезней, семь областей подземного мира, закрытых семью дверями, и т. д. Семь небесных тел перемещались по небосводу. А неведомый греческий философ, современник Фалеса и Анаксимандра, учил, следуя шумерам и вавилонянам, что все должно и по внешней форме и по своей внутренней сущности проявлять число 7, и насчитывал семь сфер Вселенной (сферы чистого эфира, звезд, Солнца, Луны, воздуха, воды и земли). Некоторые ученые думают, что мистическая роль семерки связана с тем, что когда-то люди умели считать только до шести, а число семь заменяло понятие много (ведь и сейчас мы говорим "семеро одного не ждут", "семь раз отмерь, один раз отрежь", "один с сошкой, семеро с ложкой" и т. д.).

Но выражать очень большие числа не могли ни египетские, ни греческие ученые, так как не владели идеей позиционной записи чисел. Вавилоняне же, которые владели этой идеей, относились к математике слишком утилитарно, чтобы заниматься такими далекими от практики вопросами, как, например, подсчет числа песчинок на берегу моря. Любопытно, что согласно древнеегипетским "Текстам пирамид" перевозчик в загробном мире экзаменует душу умершего царя и проверяет, умеет ли она считать до десяти. На это он получает стихотворный ответ, в котором по порядку перечисляются все пальцы. Это, несомненно, отголосок гораздо более древнего времени, когда даже умение считать на пальцах казалось чем-то граничащим с магией.

И когда люди уже научились выражать числами количество воинов в армии или хлебов, необходимых для прокормления рабов, которые возводили колоссальные храмы и пирамиды, они еще не знали чисел, носящих сейчас названия миллиард, триллион, квадрильон и т. д. Чтобы дать представление о громадных числах, они прибегали к сравнениям: "сколько песка и пыли", "как число песку на бреге морском", "как вес горы, взвешенной на весах", "как листьев на деревьях". Но самый лучший тогдашний ученый не смог бы сказать, например, чего больше:

песчинок на морском берегу или листьев в лесу.

В Древней Греции метод называния очень больших чисел был создан Архимедом лишь в III в. до н. э.( то есть через два с половиной столетия после того, как философы начали обсуждать понятие беспредельности. В сочинении "Псаммит" ("Исчисление песчинок") он развил систему счисления, позволявшую называть числа до 10^8*1016. Насколько громадно это число, видно из того, что всю нашу Метагалактику можно было бы плотно набить не более чем 10¹⁵⁰ нейтронами. Если записать число Архимеда в десятичной системе счисления по 400 цифр на каждом метре бумажной ленты, то луч света шел бы вдоль такой ленты около восьми суток.

Но как ни громадно число Архимеда, оно все же, как и все числа, конечно. Записать весь бесконечный ряд натуральных чисел невозможно даже на ленте, смотанной в клубок размером со всю нашу Метагалактику. Нельзя записать его и на ленте, смотанной во столько подобных клубков, каково число Архимеда.

Тягу к большим числам испытывали и древние обитатели Индии. В их сказаниях рассказывается, например, о битвах, в которых приняло участие 10²³ обезьян, об испытаниях Будды, в ходе которых он называл громадные числа, и о многих таких же вещах. Веселой игре с числами не мешало то обстоятельство, что вся Солнечная система по смогла бы вместить столько обезьян - в ней находила свое воплощение идея о бесконечности, завораживавшая не только греков, но и индийцев. И Архимед, и индийские математики испытывали восторг от мысли, что создано символическое исчисление, позволяющее на небольшой восковой дощечке или листе папируса выразить столь необъятные числа и выйти за пределы данного наглядным созерцанием.

Загадочные апории^*. Идея бесконечности проникала в науку не только в связи с вопросами о том, есть ли границы у Вселенной, и было ли начало, и будет ли конец мира. Одним из самых жгучих вопросов, над которым билась мысль древнегреческих философов, явилось устройство мира в малом. Повседневный опыт учил, что вынутый из печи хлеб можно разделить между двумя, тремя, от силы десятью участниками трапезы, а если раскрошить его, то получится все же не более мириады, то есть десяти тысяч крошек. Можно ли делить далее этот хлеб, есть ли вообще предел для делимости материальных предметов на части? Ответить на этот вопрос, опираясь только на опыт, было невозможно. Здесь речь шла о столь мелких частицах, что разглядеть их не смог бы и сам рысьеглазый Линией, легендарный впередсмотрящий на корабле аргонавтов. Поэтому вопрос о пределе делимости вещей перешел из сферы опыта в сферу умозрительных рассуждений.

^* (Апория - кажущееся трудно разрешимым, непреодолимым логическое затруднение.)

Одни философы утверждали, что предела делимости вещества нет. Анаксагор говорил, что "в малом не существует наименьшего, но всегда есть еще меньшее. Ибо то, что существует, не может перестать существовать от деления, как бы далеко ни было продолжено последнее". Он считал, что непрерывное не может состоять из дискретных элементов, которые "отделены друг от друга и как бы отрублены друг от друга ударами топора". Надо думать, что собрание отдельных точек представлялось Анаксагору и его сторонникам чем-то вроде кучи пыли, а непрерывное - чем-то вроде бронзового или железного меча.

Другая школа, ведшая свое начало от пифагорейцев, полагала, что существуют наименьшие частицы вещества - атомы, которые уже далее не делятся в силу своей твердости (атом и значит по-гречески "неделимый"). Эти идеи были развиты Левкиппом^* и Демокритом. Атомисты ввели понятие и о неделимых частях пространства (амерах), не имеющих ни частей, ни размеров. Некоторые ученые полагают, что эти идеи восходят к Демокриту, другие приписывают их Эпикуру^**. Решить этот спор весьма затруднительно, так как до нас дошли лишь скудные отрывки из многочисленных сочинений Демокрита.

^* (Левкипп (предположительно 500-440 до в. э.) - древнегреческий философ, атомист.)

^** (Эпикур (ок. 341-271 до н. э.) - древнегреческий философ, атомист.)

Борьба между двумя школами философов обострилась после того, как в середине V в. до н. э. греческий философ Зенон Элейский^* показал, к каким парадоксальным следствиям ведет при неосторожном обращении предположение о безграничной делимости пространства и времени. Наиболее известны апории Зенона "Стрела" и "Ахиллес и черепаха". В первой из них доказывалось, что... летящая стрела неподвижна. Ведь, говорил Зенон, стрела, прежде чем попасть в цель, должна пролететь половину пути, а до этого - одну четверть пути, еще ранее - одну восьмую пути и т. д. А так как пространство безгранично делимо, то процесс деления пополам никогда не окончится. Поэтому стрела никогда не начнет движения и всегда будет неподвижна. В апории "Ахиллес и черепаха" таким же образом доказывалось, что быстроногий Ахиллес, пробегающий в минуту 10 стадиев, никогда не нагонит медлительную черепаху, делающую 1 стадий в минуту.

^* (Зенон Элейский (ок. 490-430 до н. э.) - древнегреческий философ, автор апорий, направленных против множественности, бесконечности, движения и наивного представления о континууме.)

Выводы Зенона об отсутствии движения в реальном мире опровергались повседневным опытом. Известный философ-киник Диоген^*, услышав про рассуждения Зенона, просто встал и начал ходить (этому происшествию посвящено известное стихотворение А. С. Пушкина "Движенья нет, сказал мудрец брадатый..."). Тем не менее аргументы Зенона показали, что представления о бесконечности, господствовавшие в тогдашней математике, были весьма наивны. В частности, Зенон впервые показал, что отрезок можно разложить на бесконечное множество частей, каждая из которых имеет ненулевую длину. Если заменить геометрический отрезок конечным отрезком времени, то из его рассуждений вытекало еще более парадоксальное утверждение: за 1 час можно произнести названия всего бесконечного ряда натуральных чисел. Для этого достаточно в течение первого получаса назвать первое число, в течение следующей четверти часа - второе число, за следующую восьмую долю часа - третье число и т. д. Получалось, что бесконечное можно поместить в конечном - бесконочный числовой ряд в конечном промежутке времени.

^* (Диоген Самосский (ок. 414-323 до н. э.) -древнегреческий философ.)

Разумеется, реальное осуществление такой попытки невозможно - ведь уже число 100 придется произносить за 2^-100 часа, а самый быстрый из процессов, известных современной науке, длится неизмеримо дольше. Достичь такой быстроты невозможно и потому, что никакая информация не может передаваться со скоростью, большей, чем скорость света, а при попытке делить пространство на все более мелкие части начинают проявляться его квантовые свойства. Но ведь все это соображения, лежащие в области свойств реального мира, а Зенон, как мы бы теперь сказали, исследовал одну из математических моделей этого мира, модель, в которой допускалось неограниченное деление пополам и отрезков, и промежутков времени, так что для него доводы физиков роли не играли.

Па протяжении веков много раз менялось отношение к апориям Зенона. Иногда казалось, что они полностью опровергнуты, но внимательный анализ показывал, что на каждом уровне знаний всегда остается что-то невыясненное, какой-то зародыш новых трудностей, новых противоречий и нового знания. Известный специалист по теории бесконечных множеств и основаниям математики А. Френкель^* писал по этому поводу:

^* (Френкель Абрагам (1891-1965) немецкий математик, автор работ по математической логике.)

"Преодоление пропасти между областью дискретного и областью непрерывного, или между арифметикой и геометрией, есть одна из главных,- пожалуй, даже самая главная проблема оснований математики... Характер рассуждений теперь, конечно, изменился, но трудности, как и прежде, возникли в связи с пропастью между дискретным и непрерывным - этим неизменным камнем преткновения, играющим в то же время чрезвычайно важную роль в математике, философии и даже физике".

Позднее мы познакомимся с другими парадоксами бесконечного , по сравнению с которыми апории Зенона могут показаться весьма наивными. Но известный советский философ Г. И. Наан^* заметил, что, возможно, человечество никогда не сможет опровергнуть элейского философа на все сто процентов, поскольку бесконечность неисчерпаема, а Зенону удалось схватить в наивной, но гениальной форме три вечные проблемы, тесно связанные друг с другом и с проблемой бесконечности: проблему ничто, проблему непрерывности и проблему существования. Не случайно Аристотель называл Зенона "основателем диалектики", а Гегель видел в нем родоначальника диалектики в современном смысле слова.

^* (Наан Густав Иоганович (р. 1919) - советский философ, занимающийся философскими проблемами естествознания.)

Не обошлось, конечно, и без попыток использовать апории Зенона на пользу идеализма. Один видный немецкий философ-идеалист сказал даже, что в этих апориях бесконечность выступает как растворитель действительности.

Мы не будем сейчас подробнее останавливаться на роли апорий Зенона в физике и философии.

Для математики их роль состояла в том, что они вскрыли противоречивость дискретного и непрерывного, показали недопустимость легкомысленного обращения с бесконечностью. После Зенона нельзя уже было по примеру софиста Антифонта^* считать круг многоугольником с бесконечным числом сторон и таким путем вычислять его площадь. Началась эпоха изгнания бесконечного из математики.

^* (Антифонт (2-я половина V в. до н. э.) - древнегреческий философ-софист.)

Одну из отчаянных попыток избежать бесконечных процессов в геометрии предпринял Демокрит. Он попробовал построить геометрию на основе своего учения об атомах. Если бы эта попытка удалась, геометрия приняла бы совсем иной вид. Но еще до появления на свет Демокрита в школе Пифагора было доказано, что сторона квадрата несоизмерима с его диагональю. А этого никак не могло случиться, если бы и сторона квадрата и его диагональ состояли из конечного числа неделимых частей. Кроме того, хотя Демокрит и сумел своим методом вычислить объем пирамиды, он не мог понять, равны ли соседние сечения пирамиды - если они равны, то пирамида не может сужаться к вершине, а если они различны, то пирамида шершава. Поэтому его учебник геометрии был вытеснен знаменитыми "Началами" Евклида, основанными на идее безграничной делимости пространства, а философам пришлось искать иные пути для опровержения апорий Зенона.

На зыбкой почве. Много размышлял о бесконечности и ее свойствах один из величайших философов древности Аристотель. Говоря в своих сочинениях об этом предмете, он предупреждает, что здесь приходится ходить по очень зыбкой почве. Слишком много противоречий накопилось вокруг этого понятия со времен Зенона и Демокрита. Поэтому Аристотель признавал, что "много невозможного следует и за отрицанием существования бесконечного, и за признанием". Он указывал на пять оснований, приводящих к мысли о существовании бесконечности. Четырьмя из них были: бесконечность времени, бесконечное разделение величин, используемое в математике, необходимость бесконечности, чтобы не иссякли возникновение и уничтожение, и то, что конечное всегда граничит с чем-нибудь, а потому не может быть предела конечному. Самым же важным основанием Аристотель считал пятое, а именно что мышление ни на чем не останавливается: и число кажется бесконечным, и математические величины, и то, что лежит за небом. А если лежащее за небом бесконечно, говорил он, то существует множество миров.

И все же, несмотря на такие веские доводы, Философ (так обычно называли в древности Аристотеля) отказался принять идею о существовании бесконечного мира, сказав, что в вопросе о бесконечном доверять мышлению нельзя. Мы не будем следовать за всеми тонкостями рассуждений Аристотеля, в которых он анализирует различные следствия из предположения о существовании бесконечности.

Наиболее важно для нас проведенное им различение двух видов бесконечности: актуальной и потенциальной, то есть, иначе говоря, существующей и становящейся. Примером актуальной бесконечности может служить совокупность частей отрезка, подвергнутого разбиению по Зенону, а примером потенциальной бесконечности - развивающийся во времени процесс деления этого отрезка. Кроме того, Аристотель различал виды бесконечности, называемые сейчас экстенсивной и интенсивной. Первая из них возникает при последовательном и безграничном добавлении новых предметов, а вторая - при безграничном углублении в строение изучаемого объекта.

Аристотель признавал существование лишь потенциальной бесконечности и говорил: "Бесконечность не существует актуально, как бесконечное тело или величина, воспринимаемая чувствами... Бесконечное существует потенциально, бесконечное есть движение...".

Аргументы же Зенона он отвергал, говоря, что движущееся движется, не считая. Разумеется, отвергал Аристотель и предположения о бесконечности Вселенной, считая ее ограниченной крайней сферой, за которой уже нет ни тела, ни места. В то же время в отличие от Платона, думавшего, что мир создан неким демиургом (творцом), Аристотель утверждал несотворимость и вечность мира (впоследствии это навлекло на него упреки многих богословов).

После Аристотеля было признано, что "наука истинна лишь постольку, поскольку основывается на предположении, что непрерывное не состоит из неделимого".

Пришлось и математикам отказаться от использовании понятия бесконечности в своей науке. Например, в "Началах" Евклида оно не используется даже там, где было бы вполне естественно. Евклид не говорит даже, что простых чисел бесконечно много, а утверждает лишь, что их больше, чем любое заранее заданное натуральное число. Он никогда не пользуется движениями бесконечной плоскости, а передвигает лишь треугольники и другие конечные фигуры, да и этими движениями старается пользоваться поменьше - после Зенона понятие движения считалось логически ненадежным.

Чтобы избежать использования бесконечности, предшественник Евклида греческий математик Евдокс^* выдвинул особую аксиому, которая по сути дела означала, что не существует ни бесконечно малых, ни бесконечно больших величин: любая величина, повторенная достаточно много раз, может превзойти любую другую величину. Эта аксиома и лежала в основе метода исчерпывания, с помощью которого Евклид и Архимед доказывали теоремы о площадях и объемах.

^* (Евдокс Книдский (ок. 408- ок. 355 до н. э.) - древнегреческий математик и астроном, создатель теории несоизмеримых величин и "метода исчерпывания" для доказательства теорем о площадях и объемах.)

Возрождение бесконечности. Последние столетия античной цивилизации характеризуются упадком науки, распространением суеверий, веры в чудеса и знамения. Постепенно утрачивается устная традиция, позволявшая понимать сложные умозаключения великих ученых периода расцвета, падает авторитет науки и возрастает доверие к различного рода магам, чудодеям и пророкам. Торжество христианского вероучения завершило этот процесс медленного умирания античной философии и науки. В 415 г. н. э. толпа озверевших христианских фанатиков, натравленная александрийским епископом Кириллом, растерзала последнюю представительницу античной культуры Гипатию^* и сожгла Александрийскую библиотеку, хранившую сокровища древней культуры.

^* (Гипатия из Александрии (370-415) - философ, математик и астроном. По наущению архиепископа Кирилла зверски растерзана толпой христианских фанатиков.)

С тех пор на долгие столетия философия становится служанкой богословия, возрождаются древние суеверия о том, что плоская Земля стоит на трех китах. Лозунгом времени становятся слова богослова Тертуллиана: "Верю, потому что абсурдно". Вопрос о бесконечности тоже переходит в плоскость теологии - она становится атрибутом бога.

Но постепенно вновь распространяются идеи Платона и Аристотеля, начинается сложная работа по приведению в соответствие богословских догм с учениями древних философов. И хотя наиболее ревностные богословы отвергают учения философов-язычников, все большее число ученых переходит на точку зрения, высказанную Альбертом Великим^*: "Мне нет дела до чудес бога, когда я рассуждаю о естественных вещах, следуя естественной логике". Уже в XIV в. отдельные схоласты начинают признавать вечность мира и даже смертность человеческой души.

^* (Альберт Великий (ок. 1193-1280) - немецкий философ, естествоиспытатель, богослов и логик. Пытался в теологических целях использовать учение Аристотеля.)

В спорах богословов и философов возникают новые идеи, подрывающие как религиозные догмы, так и миросозерцание последователей Аристотеля. В 1277 г. парижский епископ Этьен Тампье обрушивается на учение Философа о вечности и несотворенности Космоса и в то же время допускает идею о возможной множественности миров. Более того, он выдвигает мысль, что небесные сферы могут иметь не только круговое, но и прямолинейное движение. Но ведь это значило, что за последней сферой есть пространство! И хотя в учении Тампье нет ни слова о бесконечности космоса, первый шаг был сделан.

А Фома Брадвардин^* в XIV в. приходит даже к мысли, что может существовать пустота без материи. Более того, нашлись схоласты, которые отвергали положение Аристотеля о несуществовании актуальной бесконечности. Так называемые инфинитисты утверждали, что понятие актуальной бесконечности не содержит в себе никакого противоречия и потому такая бесконечность может существовать. Джон Баконтроп^** в начале XIV в. утверждал, что актуально бесконечной может быть любая величина: число, время, совокупность тел, а также что тело можно разделить на бесконечно много частей. Это подрывало фундамент всей космологии Аристотеля.

^* (Брадвардин Томас (1300-1349) - английский математик, автор "Трактата о континууме", впервые применил в математическом смысле слово "иррациональный".)

^** (Баконтроп Джон - английский схоласт XIV в.)

Окончательное разрушение античной космологии произошло в XV-XVI столетиях и связано с именами Николая Кузанского^* и Джордано Бруно. Первый из них развил учение о максимуме, то есть о том, больше чего ничто не может быть. Оно явилось одним из наивысших достижений диалектической мысли эпохи Возрождения и подготовило революцию не только в космологии, но и в математическом способе мышления. Например, Николай Кузанский утверждал, что прямая является окружностью бесконечного радиуса, и рассматривал не отдельные фигуры, а предельные положения фигур при том или ином изменении их формы.

^* (Николай Кузанский (1401-1464) - немецкий философ и теолог. Его работы подготовили репс-ссансный пантеизм и создали предпосылки для обоснования бесконечности Вселенной.)

Понятие бесконечности привлекло к себе внимание и астрономов. В великом творении Николая Коперника утверждается, что расстояние между Землей и Солнцем неощутимо мало по сравнению с высотой небесной тверди. Звездную же сферу он считал в высшей степени подобной бесконечному. Иногда он говорил даже, что Небо неизмеримо велико по сравнению с Землей и представляет бесконечно большую величину. Однако решение вопроса о том, что является ли Вселенная бесконечной или лишь неизмеримо большой, он оставляет другим ученым.

Последний шаг в разрушении старых догм сделал Джордано Бруно, заплативший жизнью за свой научный подвиг. Он писал: "Итак, вселенная едина, бесконечна, неподвижна... Она никоим образом не может быть схвачена и потому неисчислима и беспредельна, а тем самым бесконечна и безгранична и, следовательно, неподвижна. Она не движется в пространстве, ибо ничего не имеет вне себя, куда бы могла переместиться, ввиду того что она является всем. Она не рождается... так как она является всем бытием. Она не уничтожается, так как нет другой вещи, в которую она могла бы превратиться... Она не может уменьшаться или увеличиваться, так как она бесконечна".

Так произошло освобождение человеческого духа от сковывающих его ограничений. Дух нового времени Бруно выразил в следующих стихах:

Кристальной сферы мнимую преграду, 
Поднявшись ввысь, я смело разбиваю
И в бесконечность мчусь, в другие дали.
Кому на горе, а кому в отраду,-
Я Млечный Путь внизу вам оставляю...

Конечно, для многих этот открывшийся умственному взору новый мир был весьма неуютен - оказались разрушены небесные сферы, заключавшие в себе упорядоченный космос античности и средневековья. Мир предстал перед человеком как помещенный в ничто, окруженный этим ничто и насквозь пронизанный им. В начале XVII в. парижский парламент издал постановление, предписывавшее предавать смертной казни всех, кто выступит с полемикой против старых и общепризнанных авторов. А святейшая инквизиция провела в то же время два процесса над крупнейшим физиком и математиком того времени Галилео Галилеем и под угрозой сожжения на костре принудила к публичному отречению от идей Коперника и Бруно, а потом приговорила к пожизненному домашнему заключению.

Но времена менялись. Чтобы решать поставленные практикой задачи, ученым все чаще и чаще приходилось применять запрещенные аристотелевой наукой приемы, использовать неделимые и бесконечно малые величины. Вновь усиливается интерес к атомизму Демокрита. Используя "незаконные" приемы, Иоганн Кеплер получил формулы для объемов тел, к вычислению которых ревнители античной строгости не знали, как и подступиться. Эти методы он применил и в своих бессмертных работах, где были установлены законы движения планет вокруг Солнца. Итальянский математик Бонавентура Кавальери^*, используя идеи своего учителя Галилея, написал книгу "Геометрия, изложенная новым методом при помощи непрерывного". В ней он выдвинул принципы, позволявшие общими методами определять площади и объемы различных фигур. К концу XVII в. методы решения самых разнообразных задач, основанные на использовании бесконечно больших и бесконечно малых величин, были систематизированы и упорядочены в работах английского физика и математика Исаака Ньютона и немецкого математика и философа Готфрида Вильгельма Лейбница. Так возникло одно из самых замечательных творений человеческого разума - математический анализ (дифференциальное и интегральное исчисления). С помощью методов математического анализа можно было, зная силы, действующие на движущееся тело, определить его траекторию, в частности определить орбиты планет и комет.

^* (Кавальери Бонавентура (1598-1647) - итальянский математик, ученик Галилея, создатель метода неделимых для отыскания площадей и объемов.)

Идеи Коперника и Бруно, Галилея и Ньютона интересовали не только ученых. Французский писатель Фонтенель^* написал в конце XVII в. сочинение "О множественности миров", переведенное на многие языки. Немецкий поэт XVIII в. Альберт фон Галлер писал:

Нагромождаю чисел тьму, 
Мильоны складываю в гору, 
Ссыпаю в кучу времена, 
Миров бесчисленных просторы. 
Когда ж с безумной высоты
Я на тебя взгляну, то ты - 
Превыше не в пример 
Всех чисел и всех мер: 
Они лишь часть тебя.

^* (Фонтенель Бернар (1657-1757) - французский литератор и популяризатор науки, один из пионеров просветительской философии.)

В России новые идеи пропагандировал великий основатель русской науки и поэт Михаил Васильевич Ломоносов, выразивший идею бесконечности мира во вдохновенных строках:

Открылась бездна, звезд полна, 
Звездам числа нет, бездне - дна.

А поэт А. П. Сумароков изложил эти идеи в ...переводе библейских псалмов. Его соперник Василий Тредьяковский тут же написал донос в святейший синод: "Читая сентябрьскую книжку "Ежемесячных сочинений" 1755 года, нашел я, именованный, в ней оды духовные, сочиненные г. полковником. Александром Петровым, сыном Сумароковым, между которыми и оду, написанную из псалма 106; а в ней увидел, что она с осмыя строфа по первую на десять включительно говорит от себя, а не из псаломника, о бесконечности вселенной и действительном множестве миров, а не о возможном по всемогуществу божиему".

Получив этот донос, святые отцы потребовали от императрицы Елизаветы запрещения журнала "Ежемесячные сочинения", в котором, как они писали, "вере святой (много) противного имеется, особенно некоторые переводы и сочинения находятся, многие, а инде и бесчисленные миры быти утверждающие, что и св. писанию и вере христианской крайне противно есть и многим неутвержденным душам причину к натурализму и безбожию подает".

Но шел восемнадцатый век, и императрица оставила покорнейшее прошение святейшего синода "без последствий".

Мир Ньютона. К концу XVII в. и в астрономии, и в физике, и в математике полную победу одержали идеи, так или иначе связанные с применением бесконечности. Сложилась картина мира, управляемого геометрией Евклида и законами движения Ньютона. Ученые полагали, что, зная положение всех материальных тел в данный момент времени, они смогут предсказать их положение в любой последующий момент - ведь для этого надо лишь решить соответствующие дифференциальные уравнения.

При этом два основоположных камня, на которых возводилось все здание, не имели ничего общего друг с другом. Бесконечное пространство никак не соотносилось с наполнявшей его материей, оно было лишь сценой, на которой разыгрывалась мировая драма. По самой своей сущности это пространство безотносительно к чему бы то ни было внешнему оставалось всегда одинаковым и неподвижным - оно не изменилось бы даже, если бы вся материя неожиданно исчезла. Как писал по этому поводу А. Эйнштейн, "Ньютон обнаружил, что наблюдаемые геометрические величины (расстояния между материальными точками) и их изменения во времени в физическом смысле не характеризуют полностью движения... Следовательно, кроме масс и изменяющихся во времени расстояний между точками существует еще нечто такое, что определяет происходящие события; это "нечто" он воспринимал как отношение к абсолютному пространству".

Успехи ньютонианских механики и астрономии сделали предложенную им картину мира общепринятой. Какие-либо сомнения в ней стали считаться чем-то антинаучным.

Картину Вселенной, принимавшуюся всеми в XVIII в., знаменитый немецкий философ Кант описал следующим образом: "В бесконечной дали существует еще много таких звездных систем, и части ее находятся во взаимной связи... Мы видим первые члены непрерывного ряда миров и систем, и первая часть бесконечной прогрессии уже дает нам представление, каково целое. Здесь нет конца, здесь бездна подлинной неизмеримости... Мировое пространство наполнено мирами без числа и без конца...".

Следует отметить, что признание бесконечности Вселенной мирно уживалось в уме Канта и большинства его современников с верой в бога. А некоторые богословы считали, что для сотворения бесконечной Вселенной нужен более могущественный бог, чем для творения конечного мира, и потому усматривали в бесконечности Вселенной "доказательство всемогущества божия". Понадобились полувековая деятельность Вольтера и энциклопедистов, грозы французской революции, чтобы Лаплас смог ответить Наполеону на вопрос, почему в его сочинении о небесной механике не упоминается бог: "Ваше Величество! У меня не возникла необходимость в этой гипотезе".

Новые осложнения. Не зря все-таки Аристотель предупреждал о зыбкости и неясности понятия бесконечности, об осложнениях, к которым оно может привести. Вскоре после создания ныотонианской физики и математического анализа в этих науках возникли первые осложнения.

Ученики и последователи Ньютона и Лейбница с необычайной легкостью пользовались расплывчатыми и полными непостижимой загадочности понятиями бесконечно малого и бесконечно большого, решая с их помощью сложнейшие задачи астрономии, физики и механики. Запросто складывали они бесконечные множества слагаемых, не колеблясь, переносили на такие суммы правила действий над конечными суммами. И хотя основные понятия нового исчисления казались туманными для математиков, воспитанных на античной строгости, практические успехи нового исчисления заставляли всех забывать об этом. "Идите вперед, и вера к вам придет", говаривал своим ученикам видный французский математик XVIII в. Д'Аламбер^*.

^* (Д'Аламбер Жан (1717-1783) - французский математик, механик и философ, один из создателей математической физики.)

Однако к концу XVIII в. появились первые признаки неблагополучия - стали накапливаться случаи, когда некорректное применение бесконечно малых и бесконечно больших величин приводило к парадоксам. Поэтому в начале XIX в. эти величины были вновь изгнаны из математики и их место заняла идея предела. Громадную роль здесь сыграли работы Нильса Хенрика Абеля^*, Огюстена Когаи^** и Карла Фридриха Гаусса^***, которого его современники называли "princeps mathematicorum" (первый среди математиков). Для отношения Гаусса к понятию бесконечности характерен следующий отрывок из его письма к Шумахеру^****, написанного в 1831 г.: "...Я протестую против употребления бесконечной величины как чего-то завершенного, что в математике никогда недопустимо. Бесконечность не нужно понимать буквально, когда речь идет собственно о пределе, к которому сколь угодно близко приближаются определенные отношения, когда другие принимаются неограниченно возрастающими".

^* (Абель Нильс (1802-1829 ) - норвежский математик, доказал невозможность решения уравнений 5-й степени в радикалах, один из создателей современных критериев строгости рассуждений в математическом анализе.)

^** (Коши Огюстен (1789-1857) - французский математик, создатель теории функций комплексного переменного. Построил математический анализ на основе понятия предела.)

^*** (Гаусс Карл (1777-1855) - крупнейший немецкий математик XIX столетия. Получил ряд результатов фундаментального значения в алгебре, геометрии, теории чисел, математическом анализе.)

^**** (Шумахер Генрих (1780-1850) - немецкий астроном.)

Возникли осложнения и в космологии. Естественное предположение о равномерном распределении звезд в бесконечном пространстве неожиданно привело к парадоксу. Оказалось, что их суммарная светимость должна была бы оказаться такой, как если бы в каждой точке неба сверкало по Солнцу. Такую картину много столетий тому назад представил себе индийский поэт, воскликнувший:

Силой безмерной и грозной небо б над нами сияло, 
Если бы тысяча Солнц разом на нем засверкала.

Кроме этого парадокса, получившего название фотометрического, возник другой, названный гравитационным. Оказалось, что если бы в бесконечной Вселенной была лишь конечная масса материи, то вся эта материя должна была бы собраться в одном месте, в один ком. А если суммарная масса бесконечна, то при равномерном распределении произошло бы взаимное уравновешивание сил тяготения.

Оба эти парадокса можно устранить, предположив, что материя распределена во Вселенной неравномерно. Но это ведет к гипотезе о существовании центра Вселенной, что не менее удивительно, чем конечность массы во Вселенной. А кроме того, как показали современные наблюдения, в нашей Метагалактике материя распределена более или менее равномерно.

Как фотометрический, так и гравитационный парадоксы оказались устранены лишь после того, как в XX в. была создана новая теория о строении Вселенной, основанная на общей теории относительности Эйнштейна. Прежде чем рассказывать о новых представлениях, сделаем еще один экскурс в математику.

Кривое пространство. В своем романе "Астронавты" писатель-фантаст Станислав Лем писал: "Картина звездного неба менялась очень быстро. Снимки, сделанные еще вчера, не совпадали со снимками, сделанными сегодня. Казалось, что какая-то таинственная сила раздвигает звезды, словно они являются крапинками на поверхности воздушного шарика, который раздувается все сильнее и сильнее. Гравитолог Звездной экспедиции уже несколько дней не отходил от вычислительной машины. Экспедиция приближалась к тяжелой звезде, сильно искривлявшей окружающее пространство. Для определения курса корабля было необходимо непрерывно вычислять эту кривизну. Это была серьезная проверка. Люди впервые сталкивались со столь сильными полями тяготения, со столь большой кривизной. Уравнения, полученные когда-то Эйнштейном, держали теперь экзамен. От них зависел успех экспедиции и даже сама жизнь ее участников".

Наиболее непонятными в этом отрывке для читателя, незнакомого с современной математикой, являются слова о кривизне пространства - вообразить себе кривое пространство куда труднее, чем кривую линию или поверхность. Не зря, когда во второй половине XIX в. возникло это понятие, была сложена эпиграмма:

Die Menschen fassen kaum es, 
Das Krummungsmass des Raumes

(люди никак не могут понять, что такое мера кривизны пространства).

Обычные возражения против искривленности пространства таковы. Кривую линию невозможно совместить с прямой и приходится располагать на плоскости или в пространстве. Точно так же и кривую поверхность невозможно поместить на плоскости - для этого нужно по крайней мере трехмерное пространство. Следовательно, и искривленное трехмерное пространство должно лежать в каком-то объемлющем его пространстве четырех, а то и пяти измерений. А так как никто четырехмерного пространства не наблюдал, то пространство, в котором мы живем, никак не может быть искривленным. Некоторые философы добавляли к этим рассуждениям всякие слова об идеализме, фидеизме и т. д. Зато авторам научно-фантастических рассказов идея четырехмерного пространства очень понравилась. Во многих рассказах и повестях Уэллса происходят путешествия в четвертом измерении.

На самом деле искривленность пространства совсем не связана с четвертым измерением, а является, так сказать, его внутренним делом. И установить искривленность можно не выходя из этого пространства, а лишь проводя измерения внутри него.

Для того, чтобы читателю было яснее, как это делается, расскажем сначала, как установить кривизну поверхности, не покидая ее, а лишь измеряя расстояния между ее точками.

Геометрия на Ялмезе. В течение многих тысячелетий люди думали, что Земля плоская. Однако наблюдения за тенью Земли во время лунных затмений привели древнегреческих ученых к мысли о шарообразности Земли. Эратосфену удалось даже с довольно большой точностью измерить ее радиус. Но после того, как снова воцарилась мысль, что Земля плоская, для доказательства шарообразности Земли понадобилось кругосветное путешествие Магеллана.

А теперь представьте себе планету Ялмез, где живут разумные существа, но небо закрыто вечной пеленой облаков, а океанские путешествия по тем или иным причинам невозможны. Смогли бы жители этой планеты узнать, что кости, со всех сторон окруженном водой, а на сфере? Иными словами, было ли необходимо путешествие Магеллана для того, чтобы доказать шарообразность Земли?^*

^* (Разумеется, автор не ставит под сомнение ни географическую ценность путешествия Магеллана, ни его историческое значение. Речь идет только о чисто математическом вопросе: как установить искривленность земной поверхности, не совершая кругосветных путешествий?)

Чтобы понять, как возникает идея кривизны поверхности, проследим за ходом развития геометрии на планете Ялмез. Геометрия возникает как экспериментальная наука, как теоретическое обобщение многовековых наблюдений над свойствами пространства. Поскольку мы условились считать, что небо планеты покрыто облаками, геометрам Ялмеза пришлось вести наблюдения лишь на поверхности планеты. Оказалось, что среди всех линий, соединяющих две точки этой поверхности, всегда есть наикратчайшая (рис. 1). Наикратчайшие линии и были названы "отрезками прямых". Разумеется, наблюдатель, который посмотрел бы на планету со стороны, сказал бы, что эти линии совсем не прямые, а кривые - это дуги сечений сферы диаметральными плоскостями. Но ялмезяне не могли посмотреть на свою планету со стороны и считали наикратчайшие линии, проведенные на поверхности, прямыми (впрочем, ведь и мы часто говорим "дорога прямая, как стрела", хотя на самом деле она идет по дуге диаметрального сечения).

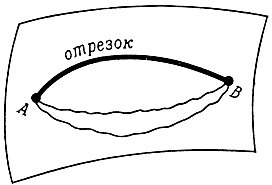
Рис. 1

Затем установили свойства этих "прямых". В самом начале наблюдению была доступна лишь малая часть планеты, а точность измерения оставалась очень небольшой. Поэтому в пределах точности измерения свойства "прямых" на поверхности планеты были такими же, как свойства прямых на плоскости: через две точки проходила одна и только одна "прямая", две "прямые" пересекались в одной и только одной точке (вторая точка пересечения, диаметрально противоположная первой, была недосягаема для наблюдателей). Наконец, ялмезянские геометры были уверены, что их "прямые линии" бесконечны. Самая мысль, что при движении по "прямой" в одном и том же направлении они вернутся в исходную точку, казалась дикой, непонятной и противоречащей здравому смыслу. И ялмезянские ученые были убеждены, что поверхность их планеты бесконечна, а тех, кто выдвигал иные идеи, обвиняли во всех смертных грехах...

Дальнейшее изучение свойств "прямых" показало, что в пределах точности измерения сумма углов любого треугольника равна 180°, что квадрат гипотенузы равен сумме квадратов катетов и т. д. Иными словами, жители Ялмеза построили геометрию Евклида и считали, что она полностью приложима к поверхности их планеты.

Вскоре, однако, им пришлось убедиться, что это не так. По мере развития техники удавалось измерить все большие и большие куски суши (мы договорились, что океанских плаваний ялмезяне совершать не могли). И эти измерения вступили в противоречие с евклидовой геометрией. Чтобы понять, в чем здесь дело, возьмем на сфере три точки A, B и C (рис. 2, а). Эти точки можно соединить "отрезками прямых", а по нашему - дугами меридианов AB и AC и дугой экватора BC. В результате получается треугольник ABC. Легко видеть, что все три угла этого треугольника прямые. Значит, сумма его углов равна 270°, а не 180°, как полагается по геометрии Евклида. На 90° больше, чем нужно.

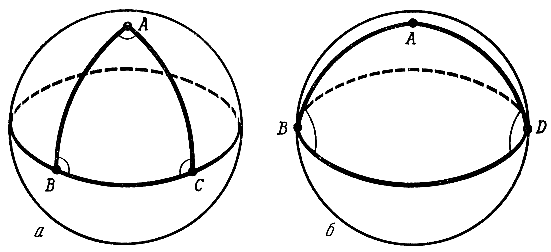
Рис. 2

У других треугольников избыток суммы углов был бы другой. Например, у треугольника ABD (рис. 2, б) углы B и D равны 90°, а угол BAD равен 180°. Сумма углов этого треугольника равна 360° - на 180° больше, чем нужно. В дальнейшем число α+β+γ - 180°, где α, β, γ - углы сферического треугольника, мы будем для краткости называть избытком сферического треугольника.

Поворот параллельных. Но не только наличие избытка у треугольников показало жителям Ялмеза, что они живут не на плоскости, а на кривой поверхности. Неверной оказалась и теорема Пифагора. Например, у треугольника ABC угол А равен 90°, а все его стороны равны друг другу. Вообще, здесь трудно разобрать, где гипотенуза, а где катеты - все углы прямые.

К неожиданным результатам привело и изучение параллельных прямых на поверхности планеты. Ведь если провести на плоскости замкнутую линию, а потом перемещать вдоль нее отрезок так, чтобы он оставался все время параллелен самому себе, то отрезок вернется в исходную точку, не изменив направления (рис. 3, а). Измерения на малых участках поверхности планеты, казалось бы, подтверждали этот результат (параллельными ялмезяне считали прямые, перпендикулярные одной и той же прямой).

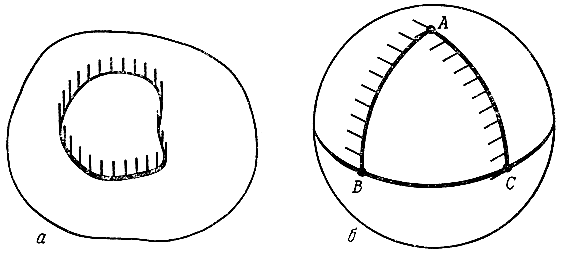
Рис. 3

Ио измерения больших участков поверхности привели совсем к иным результатам. Возьмем, например, треугольник ABC (рис. 3, б) и проведем в точке A "отрезок", перпендикулярный AB. Будем переносить этот отрезок вдоль контура треугольника ABC, следя за тем, чтобы он оставался все время параллельным самому себе. Когда мы придем в точку B, то получим отрезок, направленный по экватору. Так как экватор сам является "прямой", то после параллельного переноса в точку C отрезок снова будет направлен по экватору. А когда мы перенесем его еще по меридиану CA, то получим отрезок, повернутый на 90° относительно первоначального направления (то есть как раз на величину избытка треугольника ABC). А если бы мы переносили отрезок по контуру треугольника ABD на рис. 2, б, то он повернулся бы на 180°.

Вообще, при параллельном переносе по контуру любого сферического треугольника отрезок поворачивается на угол, равный избытку этого треугольника. Любопытный результат получается, если переносить отрезок вдоль экватора. На первый взгляд кажется, что он возвратится в исходную точку, не повернувшись. Но это неверно. Если все время сносить движущийся отрезок в одну и ту же точку - полюс сферы, то мы увидим, что он повернулся на 360° (рис. 4). Но это и неудивительно. Дополним экватор дугой меридиана АВ, пробегаемой в обоих направлениях. Мы получим "треугольник" ABA. В этом треугольнике два угла прямые, а третий равен 360°. Поэтому и его избыток равен 360°.

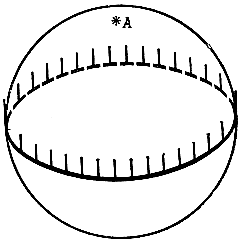
Рис. 4

Измерение кривизны. Итак, измеряя сумму углов треугольника, наблюдая за поворотом параллельных при переносе по замкнутому контуру, проверяя теорему Пифагора, жители планеты убедились, что они живут не на плоскости, а на какой-то искривленной поверхности. За меру кривизны некоторого участка поверхности они приняли угол поворота отрезка, параллельно перенесенного вдоль границы этого участка. Эту кривизну можно было считать и по-другому: разбить участок на треугольники и сложить избытки всех треугольников. Ведь, если два треугольника объединяются в один, то их избытки складываются.

Оказалось, что чем больше площадь участка, тем сильнее он искривлен. Точнее говоря, избыток любого треугольника оказался пропорционален его площади:

мы будем измерять углы не в градусах, а в радианах; при таком измерении сумма углов плоского треугольника равна π). Отсюда был сделан вывод, что кривизна поверхности на единицу площади всюду одна и та же. Число к и приняли за меру кривизны.

Но среди всех поверхностей есть только одна поверхность, для которой избыток треугольника на единицу площади всегда один и тот же - это сфера. Поэтому геометры Ялмеза установили, что они живут на сфере, а не на какой-нибудь другой поверхности. Без особого труда удалось даже найти радиус этой сферы. Ведь если число к не зависит от выбора треугольника, его достаточно подсчитать для одного треугольника. Возьмем, например, треугольник ABC на рис. 2, а. Его избыток равен 90°, или, в радианной мере, ^π/₂. Площадь же этого треугольника равна ¹/₈ площади сферы, то есть ^πR2/₂. Подставляя эти значения в формулу (1), получаем, что k = ¹/_R², а потому для любого сферического треугольника

где α, β, γ - его углы, S - площадь и R - радиус сферы. Полученная формула позволяет определить радиус сферы путем измерения углов и площади треугольника. Разумеется, этот способ не очень удобен, так как требует весьма большой точности измерения углов. Для измерения радиуса Земли прибегли к иному способу - измерению длины дуги меридиана, что потребовало наблюдений за звездами.

Гауссова кривизна. Формула (1) определяет кривизну к поверхности сферы, отнесенную к единице площади. Как мы видели, она равна ¹/_R². Иными словами, чем больше радиус сферы, тем меньше искривлен участок ее поверхности, имеющий единичную площадь; поверхность мяча искривлена гораздо больше, чем поверхность Земли.

Гаусс предложил таким же образом измерять кривизну любой поверхности. На любой поверхности можно строить геометрию точно так же, как и на поверхности сферы. Роль прямолинейных отрезков играют при этом кратчайшие (их еще называют геодезическими) линии, то есть линии, длина которых меньше длины всех остальных линий, соединяющих данные две точки. С ними впервые столкнулись геодезисты при измерении расстояний на поверхности Земли. К слову сказать, и сам Гаусс пришел к занятиям геометрией на поверхностях после того, как он в течение нескольких лет занимался геодезическими измерениями.

Из геодезических линий можно строить треугольники, четырехугольники и т. д. При этом на любой кривой поверхности, как и на сфере, сумма углов треугольника не будет, вообще говоря, равна π. Кривизной треугольника, отнесенной к единице площади, мы снова назовем число ^{(α + β + γ - π)}/_S. Однако на произвольных поверхностях это число будет для различных треугольников различным. Более того, оно может быть для одних треугольников положительным, а для других - отрицательным (треугольники могут иметь не только избыток, но и недостаток).

Чтобы найти кривизну в какой-то точке поверхности, надо брать все меньшие и меньшие треугольники, охватывающие эту точку, и искать их кривизну, отнесенную к единице площади. В пределе мы получим кривизну поверхности в данной точке. Это определение кривизны дал Гаусс, и ее обычно называют гауссовой кривизной. Если треугольники имеют избыток, то гауссова кривизна поверхности положительна, а если сумма углов меньше π, то кривизна отрицательна.

Если поверхность выпукла, то ее гауссова кривизна во всех точках положительна, а для бублика, изображенного на рис. 5 (математики называют его тором), в одних точках гауссова кривизна положительна, а в других - отрицательна.

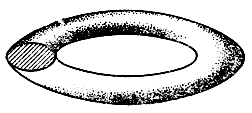
Рис. 5

Замечательным свойством гауссовой кривизны является то, что она не меняется при изгибании поверхности, то есть при ее преобразованиях, не изменяющих расстояний между точками. Отсюда ясно, например, что во всех точках цилиндра гауссова кривизна равна нулю. Ведь цилиндр получается изгибанием куска плоскости, а кривизна плоскости равна нулю. Равна нулю гауссова кривизна и во всех точках конуса, кроме его вершины.

Псевдосфера и геометрия Лобачевского. На сфере во всех точках кривизна одна и та же, и притом положительна. А есть поверхность постоянной отрицательной кривизны. Ее называют псевдосферой. Она получается следующим образом.

Представим себе, что в точке A стоит человек, который держит на поводке собаку (рис. 6). Вначале собака находится в точке O. После этого она бежит по прямой Oz с постоянной скоростью, а ее хозяин бежит вслед за ней так, что его скорость все время направлена вдоль поводка. Поэтому сначала хозяин бежит в направлении AO. Но по мере того, как собака продвигается по прямой Ox, направление бега хозяина образует все меньший угол с этой прямой, причем расстояние от бегущего человека до прямой Ox становится все меньше. На рис. 6 изображена линия, по которой бежит человек. Она называется трактрисой и обладает следующим замечательным свойством: в какой бы точке M к ней ни провести касательную, отрезок этой касательной между точкой M и осью Ox имеет одну и ту же длину.

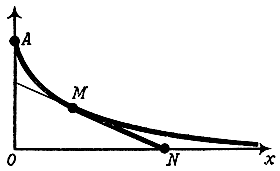
Рис. 6

Если повернуть трактрису вокруг прямой Ox, то получится псевдосфера (рис. 7). Эта поверхность замечательна тем, что геометрия на ней совпадает с геометрией на куске плоскости Лобачевского. Поэтому открытие псевдосферы было очень важным этапом в развитии неевклидовой геометрии.

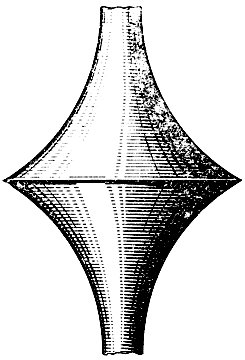
Рис. 7

Гаусс и Риман. В работах Гаусса был до конца решен вопрос о том, что такое кривизна поверхности. На повестку дня встала проблема, как определить меру кривизны пространства. Это удалось сделать одному из самых замечательных математиков XIX в.- Бернгарду Риману.^*

^* (Риман Бернгард (1826-1866) - немецкий математик, получил ряд замечательных результатов в теории функций комплексного переменного, геометрии и других областях математики. Один из создателей общего понятия многомерного пространства (риманова геометрия).)

Проблеме кривизны пространства была посвящена пробная лекция, прочитанная Риманом в 1854 г. Тогда в университетах существовал хороший обычай: начинающий преподаватель должен был прочесть лекцию для членов факультета, чтобы они могли определить его педагогические способности. Риман предложил несколько тем пробных лекций, из которых Гаусс выбрал одну, сильнее всего заинтересовавшую его - "О гипотезах, лежащих в основании геометрии". Надо полагать, что слушатели остались не слишком высокого мнения о педагогических дарованиях Римана: содержание лекции понял до конца лишь один слушатель - Гаусс.

Почти без формул и выкладок Риман развил общие идеи о многомерных многообразиях, об измерении длин в таких многообразиях, их кривизне и т. д. В лекции были поставлены интересующие до сих пор физиков-теоретиков вопросы о том, непрерывно или дискретно наше пространство, применима ли обычная геометрия к бесконечно-малым областям пространства. Глубина этих идей захватила Гаусса, и, как рассказывают очевидцы, он ушел домой в глубокой задумчивости.

Кривизна пространства. Как же ответил Риман на вопрос: что такое кривизна пространства и как она измеряется? Он применил тот же способ, каким Гаусс измерял кривизну поверхности: подсчитывал сумму углов треугольника, составленного из отрезков геодезических линий, и смотрел, на сколько она отличается от π. Однако при этом возникло осложнение: ведь в пространстве через точку можно провести много плоскостей и кривизна зависит не только от того, в какой точке ее вычисляют, но и от того, в какой плоскости лежат треугольники. Поэтому Риман говорил не о кривизне в данной точке, а о кривизне в данной точке в направлении данной плоскости.

Если для всех треугольников в пространстве сумма углов равна π, тов этом пространстве верна обычная геометрия Евклида. Такое пространство не имеет кривизны, или, как говорят, оно плоское. Если же есть треугольники, сумма углов которых больше π, то кривизна пространства в соответствующих точках положительна; если же сумма углов меньше π, то отрицательна.

Таким образом, понятие кривизны пространства не содержит в себе ничего таинственного, а указывает лишь на то, что сумма углов треугольника может отличаться от предписанного Евклидом значения. Особенно интересными являются пространства, в которых кривизна во всех точках и во всех плоскостях одна и та же. В таких пространствах (их называют пространствами постоянной кривизны) тела могут передвигаться из одного места в другое, не меняя своих размеров. Если же кривизна пространства переменна, то тело при перемещении будет менять размеры, искажаться.

Риман поставил вопрос о том, является ли искривленным реальное пространство, в котором мы живем. Он писал: "Или то реальное, что создает идею пространства, образует дискретное многообразие, или же нужно пытаться объяснить возникновение метрических соотношений чем-то внешним - силами связи, действующими на это реальное.

Решение этих вопросов можно надеяться найти лишь в том случае, если, исходя из ныне существующей и проверенной опытом концепции, основа которой положена Ньютоном, станем ее постепенно совершенствовать, руководствуясь фактами, которые ею объяснены быть не могут... Здесь мы стоим на пороге области, принадлежащей другой науке - физике, и переступать его не дает нам повода сегодняшний день".

Путешествие за кривизной. Лишь в начале XX в. начало осуществляться предсказание Римана - вопрос о кривизне пространства перешел из области абстрактных математических рассмотрений в область конкретных физических теорий. Обдумывая причину равенства инертной и гравитационной масс, великий физик Альберт Эйнштейн создал общую теорию относительности, радикально изменившую наши представления о связи материи и пространства. Если, как уже говорилось выше, в физике Ньютона пространство никак не зависело от наполнявшей его материи, то в новой теории оказалось, что пустого пространства, то есть пространства без содержащегося в нем поля, просто не существует. Пространство и время оказались существующими не сами по себе, а лишь в неразрывной связи друг с другом и только как структурное свойство поля.

Построенная Эйнштейном теория была настолько сложна и непривычна, что многие ученые отнеслись к ней с недоверием (а другие попросту не поняли). Вдобавок ко всему, кроме равенства двух видов массы, у Эйнштейна не было никаких экспериментальных доказательств своей теории. А физики обычно признают новую теорию лишь в случае, когда она не только объясняет все известные явления,; но и предсказывает новые, еще не наблюдавшиеся.

Но среди многих неожиданных и на первый взгляд парадоксальных выводов из общей теории относительности один сравнительно легко поддавался экспериментальной проверке. По этой теории притягивающие массы должны были искривлять пространство. Поэтому надо было лишь доказать экспериментально кривизну пространства.

Физическими экспериментами было давно установлено, что свет всегда распространяется так, чтобы пройти свой путь за кратчайшее время, причем скорость света в пустоте всегда одна и та же. Поэтому за геодезические линии в пространстве принимали световые лучи (в пустоте).

Теперь для определения кривизны пространства надо было измерить сумму углов треугольника, составленного из световых лучей. Однако даже для треугольников, одной из вершин которых является звезда, эта сумма в пределах ошибок наблюдения не отличается от π. Поэтому можно сказать, что если пространство в целом и искривлено, то эта кривизна очень мала. Заметим, что безуспешные попытки доказать неевклидовость реального пространства путем прямого измерения суммы углов космических треугольников предпринимали еще Гаусс и Н. И. Лобачевский^*.

^* (Лобачевский Николай Иванович (1792-1856) - русский математик, творец неевклидовой геометрии. Является также одним из создателей современного определения функции.)

Эйнштейн предложил вместо определения суммы углов космических треугольников пронаблюдать за изменением хода световых лучей. Из его теории следовало, что если сфотографировать одну и ту же звезду дважды - когда ее луч проходит далеко от Солнца и когда он проходит около Солнца, то мы заметим сдвиг ее положения, вызванный искривлением светового луча.

Впрочем, отклонение должно было иметь место и по обычной физике, но у Эйнштейна оно оказалось вдвое большим. Надо сказать, что и по новой теории отклонение было очень небольшим - меньше двух угловых секунд (под таким углом мы увидим двухкопеечную монету с расстояния в 1200 метров). Но все-таки такое отклонение можно измерить, и хотя вблизи Солнца звезда тонет в сиянии солнечных лучей, во время полных солнечных затмений соответствующие наблюдения удается провести.

Поэтому весной 1919 г. были отправлены две научные экспедиции для измерения кривизны пространства: одна на западное побережье Африки, а другая - в Северную Бразилию. Наблюдения, проведенные ими 29 мая 1919 г., полностью подтвердили предсказание Эйнштейна: смещение звезды оказалось именно таким, каким оно должно было быть по его теории. Тем самым было доказано, что материя искривляет окружающее ее пространство.

Другое доказательство искривленности пространства дали наблюдения за планетой Меркурий. Эта планета находится ближе к Солнцу, чем остальные планеты, и потому испытывает наибольшее влияние искривленности околосолнечного пространства. Из-за этой искривленности после полного оборота Меркурия вокруг Солнца его орбита немного поворачивается. Впрочем, орбита поворачивается и по другой причине - из-за притяжения планет. Поворот орбиты, вызванный притяжением планет, астрономы умели учитывать. Но их расчеты не сходились с действительностью - орбита поворачивалась быстрее, чем нужно, на 41 секунду в сто лет. Когда подсчитали по формулам Эйнштейна, на сколько поворачивается орбита из-за кривизны пространства, ответ был: на 41 секунду в сто лет. Этим была объяснена загадка, долгое время мучившая астрономов, а заодно получено новое подтверждение теории относительности.

Расширяющаяся Вселенная. После появления общей теории относительности перед астрономами встал важнейший вопрос: а как же устроено реальное пространство? Ведь если оно искривлено и кривизна его положительна, то оно может быть устроено примерно как трехмерная сфера, то есть но иметь нигде границ и в то же время иметь конечные размеры. Некоторые философы отрицали самую возможность конечности размеров реального пространства. Но их доводы не более убедительны, чем доказательства ялмезянских ученых, считавших, что они живут на бесконечной плоскости, а не на ограниченной сфере. Ответ на поставленный вопрос должны были дать не умозрительные построения, а астрономические исследования.

Первую попытку построить модель Вселенной на основе новой теории тяготения сделал сам Эйнштейн. Однако она оказалась не слишком удачной. Дело в том, что он попробовал построить модель стационарной Вселенной, не меняющейся с течением времени. Ведь еще Аристотель писал, что "в продолжение всего прошедшего времени, согласно летописям, завещаемым потомкам от поколения к поколению, мы не находим следа изменений ни во всем удаленном небе в целом, ни в одной из подходящих частей неба".

Чтобы построить стационарную модель Вселенной, Эйнштейну пришлось ввести предположение о существовании сил, отталкивающих галактики друг от друга и пропорциональных разделяющему их расстоянию. Существование таких сил не подтверждалось какими-либо известными в то время опытами. Впоследствии Эйнштейну пришлось признать предположение о таких силах отталкивания "самой грубой ошибкой в своей жизни".

Неожиданное решение предложил в 1922 г. молодой ленинградский математик Александр Александрович Фридман^*. В статье "О кривизне пространства" он доказал, что уравнения общей теории относительности имеют нестационарные решения, то есть решения, при которых Вселенная либо расширяется, либо сжимается. При этом соответственно кривизна и плотность материи должны либо уменьшаться, либо увеличиваться. Любопытно, что теоретическая физика отнюдь не была основным предметом исследований Фридмана - его главные работы лежат в области динамической метеорологии.

^* (Фридман Александр Александрович (1888-1925) - советский физик и космолог.)

Решение, полученное Фридманом, настолько противоречило установившимся взглядам на строение Вселенной, что первой мыслью ученых было предположение о допущенной им ошибке. Именно так отозвался об этой работе Эйнштейн в краткой заметке, помещенной в очередном номере того же физического журнала, где была опубликована статья Фридмана. Вскоре Эйнштейн получил подробное письмо от автора статьи, рассеявшее все сомнения. И хотя Эйнштейн был уже тогда общепризнанным главой физиков, а Фридман - начинавшим исследователем, маститый ученый ни минуты не поколебался в том, как ему следует поступить. 13 мая 1923 г. в редакцию "Физического журнала" поступило следующее письмо Эйнштейна, опубликованное под заголовком "Заметка о работе А. Фридмана о кривизне пространства": "В предыдущей заметке я критиковал названную работу. Однако моя критика, как я убедился из письма Фридмана, основывалась на ошибках в вычислениях.

Я считаю результаты Фридмана правильными и проливающими новый свет. Оказывается, что уравнения поля допускают наряду со статическими также и динамические (т. е. переменные относительно времени) центрально-симметрические решения для структуры пространства".

Позднее выяснилось, что на самом деле статических решений не существует - модель Эйнштейна была неустойчивой и потому однородная и изотропная (одинаковая во всех направлениях) модель Вселенной обязана была оказаться нестационарной.

Вслед за Фридманом многие физики и астрономы начали строить динамические модели Вселенной. Так появились модели Леметра^*, де Ситтера^** и других.

^* (Леметр Жорж (1894-1966) - бельгийский астроном и астрофизик, автор теории расширяющейся Вселенной.)

^** (Ситтер де Биллем (1872-1934) - голландский астроном, один из пионеров применения теории относительности к космологии.)

И вновь возник вопрос об экспериментальном подтверждении той или иной модели Вселенной; в частности, надо было выяснить, расширяется она или сжимается. И тут астрономы вспомнили, что еще в начале XX в. американский астрофизик В. М. Слейфер^* проводил измерения лучевых скоростей галактик. Оказалось, что 36 из 41 исследованных им галактик удаляются от нас, причем некоторые из них - со скоростью 2 000 ^км/_с (впоследствии оказалось, что остальные 5 галактик приближаются к нам из-за собственного движения Солнца в нашей Галактике). Исследования Слейфера были продолжены американским астрономом Э. Хабблом^**, который определил не только скорости галактик, но и их расстояния до Солнца. Проведенные им исследования показали, что имеет место замечательный закон: скорость удаления галактик от нас пропорциональна их расстоянию. Иными словами, быстрее всего удаляются от нас наиболее удаленные галактики.

^* (Слейфер Весто (1875-1969) - американский астроном, впервые измеривший лучевые скорости туманностей.)

^** (Хаббл Эдвин (1889-1953) - американский астроном, установил, что туманности являются звездными системами.)

Этим была убедительно доказана справедливость догадки Фридмана. Оказалось, что Вселенная действительно расширяется. Не следует думать, разумеется, что Земля является тем центром, от которого во все стороны разлетаются галактики. Просто при расширении Вселенной наблюдатель, находящийся в любой точке, увидит одну и ту же картину - разлет галактик во все стороны от точки, где он находится.

Картина расширяющейся Вселенной позволила объяснить как гравитационный, так и фотометрический парадокс. Оказалось, что свет от слишком удаленных звезд не доходит до Земли, что мы можем видеть лишь галактики, находящиеся ближе так называемого видимого горизонта. Этим объясняется и то, почему мы наблюдаем расширяющуюся, а не сжимающуюся Вселенную. В периоды сжатия Вселенной (если они существуют) фотометрический парадокс должен проявиться во всю свою силу и поступающий на Землю поток энергии будет таким, что никакая жизнь на ней не будет возможна. Иными словами, жизнь возможна лишь в периоды расширения и невозможна в периоды сжатия.

Былое и будущее Вселенной. После появления нестационарных моделей Вселенной встал ряд вопросов, над которыми сейчас работает мысль физиков-теоретиков: когда начался разлет галактик и что было до этого, будет ли это разбегание продолжаться вечно или оно сменится периодом сжатия и т. д. В настоящее время большинство ученых согласны в том, что много миллиардов лет тому назад Вселенная находилась в сверхплотном состоянии. Плотность сгустка была, по-видимому, больше, чем плотность вещества в ядрах атомов, то есть больше, чем 10^14г/_см³. Некоторые подсчеты дают величины порядка 10^93г/_см³. Ясно, во всяком случае, что материя находилась в состоянии, совершенно неведомом современным физикам, и к ней не были применимы ни законы гравитации, ни квантовая теория.

Физики-теоретики пытаются, основываясь на наблюдениях над Вселенной в современном состоянии, сделать определенные выводы о ее состоянии во времена, близкие к моменту того "большого взрыва", с которого, как они полагают, началась ее история. Они вычисляют, когда начали образовываться элементарные частицы, когда эти частицы стали складываться в атомы, как менялась температура Вселенной и т. д. На основании этих исследований было доказано, в частности, что если в начале Вселенная была "горячей", то до наших дней должно дойти так называемое реликтовое электромагнитное излучение, температура которого в разных вариантах теории принимала значения от долей градуса до 20-30 градусов Кельвина.

Советские теоретики А. Г. Дорошкевич^* и И. Д. Новиков^** рассчитали в 1964 г., насколько интенсивность реликтового излучения должна превышать в сантиметровой области спектра интенсивность других источников. Но эта работа, указывавшая на возможность решающего эксперимента, оказалась не замеченной наблюдателями. Реликтовое излучение было открыто совершенно случайно в 1965 г. при отладке радиоантенны, созданной для наблюдения за спутниками. Температура этого излучения оказалась равной 3 градусам Кельвина. Это открытие делает весьма вероятной модель горячего начального состояния Вселенной.

^* (Дорошкевич Андрей Георгиевич (р. 1937) - советский физик и космолог.)

^** (Новиков Игорь Дмитриевич (р. 1935) - советский астрофизик и космолог.)

Мы не будем подробно рассказывать, как возникли и развивались по современным представлениям звезды и галактики. Здесь много спорного, и известный физик Л. Бриллюэн^* высказался обо всех этих теориях (равно как и о теории "большого взрыва"), что "все это слишком красиво, чтобы быть истинным, и слишком невероятно, чтобы поверить в это". Тем не менее наука в настоящее время не располагает иной теорией, объясняющей такое количество загадочных явлений во Вселенной.

^* (Бриллюэн Леон (1889-1969) - французский физик, автор работ по квантовой механике, теории информации, философии науки.)

Другой вопрос, интересующий ученых, касается, разумеется, будущего Вселенной. Возможны два варианта: либо Вселенная будет неограниченно расширяться и в невероятно далеком будущем галактики разойдутся друг от друга настолько далеко, что обитатели каждой из них не будут видеть на небе остальных, либо в какой-то момент разбегание галактик остановится и сменится их сближением. Как показали подсчеты ученых, выбор между этими двумя возможностями зависит от средней плотности вещества во Вселенной. Если эта плотность меньше, чем 10^-29г/_см³, то расширение будет продолжаться вечно, а если она больше этой величины, то в какой-то момент времени начнется сжатие Вселенной. Некоторые ученые полагают даже, что это сжатие будет продолжаться, пока Вселенная не превратится вновь в сверхплотный сгусток, а потом все начнется сначала. Поневоле вспоминаешь слова Гераклита о закономерно вспыхивающем и закономерно угасающем огне.

Но какова же плотность вещества во Вселенной на самом деле? Ответить на этот вопрос довольно трудно, так как возможно, что большая часть вещества находится в состоянии, недоступном для наблюдения (так называемые черные дыры, не испускающие никакого излучения, межгалактический газ, а может быть, нейтрино, обладающие способностью пронизывать громадные массы материи, не взаимодействуя с ней). По принятым сейчас оценкам эта плотность раз в 30 меньше критического значения, так что, вроде бы, опасаться начала сжатия Вселенной не приходится. Но сейчас каждый год приносит так много новых сведений, что окончательный ответ дать преждевременно.

Бесконечна ли Вселенная? Одним из труднейших вопросов космологии, то есть физического учения об отношении всех частей Вселенной к ней как к целому, является проблема, стоящая в заголовке этого раздела. Ведь в зависимости от того, больше средняя плотность материи в Метагалактике критического значения 10^-29г/_см³ или меньше, модель Метагалактики получается открытой или закрытой. И если открытая модель может согласоваться с предположением бесконечных размеров Вселенной, то для ее закрытой модели кривизна положительна и потому размеры ограничены сверху каким-то числом. При этом никакими мыслимыми в настоящее время способами невозможно опровергнуть утверждение, согласно которому наша Вселенная в действительности является замкнутой, причем ее размеры не превышают 10²⁵ км.

Вопрос о конечности или бесконечности Вселенной осложняется еще и тем, что с точки зрения теории относительности пространство и время не существуют отдельно, а лишь как единое целое. Пользуясь этим, известный советский специалист в области космологии А. Л. Зельманов^* построил совершенно удивительные модели. В одной из них пространство, объем которого в одной системе отсчета бесконечен, в другой системе отсчета имеет конечный объем. В другом примере, наоборот, пространство, имеющее в одной из систем отсчета бесконечный объем, является частью пространства, объем которого в иной системе конечен. Аналогичные парадоксы имеют место и для времени при наблюдении за гравитационным коллапсом (охлопыванием выгоревшей звезды в точку под действием силы тяготения) - процесс, который в одной системе отсчета укладывается в конечный промежуток времени, в другой длится бесконечно долго.

^* (Зельманов Абрам Леонидович (р. 1913) - советский космолог.)

Таким образом, привычное противопоставление конечности и бесконечности в пространстве, конечности и бесконечности во времени как взаимоисключающих возможностей и вообще привычная нам постановка вопроса о конечности и бесконечности в пространстве и во времени едва ли могут считаться правильными во всех случаях.

Ситуация осложняется еще возможной неоднородностью и анизотропией (различием свойств в разных направлениях) Вселенной, которые могут привести к тому, что ее модель оказалась бы похожа не на трехмерную сферу, а на более сложные геометрические образы (вспомним, что даже среди поверхностей нулевой кривизны есть не только куски плоскости, но и такие поверхности, как цилиндры и конусы). Таким путем возникает бесконечное многообразие возможных моделей Вселенной, которое неизмеримо богаче, но в то же время и неизмеримо сложнее, чем то, что допускалось дорелятивистской космологией.

Все эти сложности показывают, что однозначный ответ на поставленный выше вопрос вряд ли возможен.

Неизмеримо осложнился и вопрос о бесконечной делимости вещества. Если в начале XX в. считали, что оно состоит из неделимых далее атомов, то после открытий Резерфорда оказалось, что атомы сами состоят из ядер и электронов. Потом были открыты протоны, еще через некоторое время - нейтроны и позитроны, и к концу 30-х годов сложилась нейтронно-протонная модель атомного ядра. Эта модель оказалась настолько удачной, что позволила решить проблему освобождения атомной энергии. Но еще до пуска первого реактора появились новые элементарные частицы - мезоны различного рода. А дальше число элементарных частиц росло чуть ли не по показательному закону - антипротоны и антинейтроны, всевозможные гипероны и антигипероны, резонансы и т. д. И при этом оказалось, что нейтроны могут превращаться в протоны, а протоны - в нейтроны, а потому для них понятие "состоит из" потеряло смысл.

Чтобы навести порядок в мире элементарных частиц, были придуманы частицы нового вида - кварки, которых, однако, никто не наблюдал, хотя с их помощью все хорошо объясняется. Они отличаются друг от друга цветом (совершенно условное название), и была создана новая область физики - хромодинамика. По новейшим воззрениям мы и не сможем никогда увидеть кварки "живьем". Дело в том, что внутри элементарных частиц между кварками действуют силы, которые возрастают по мере увеличения расстояния между ними (как растет сила натяжения пружины, когда ее растягивают). Таким образом, трудно сказать, как теперь надо понимать безграничную делимость вещества.