3. Решение Платона

Ниже приводится решение делосской задачи, приписываемое Платону. Это решение основано на следующей лемме:

Во всякой прямоугольной трапеции (рис. 3) с перпендикулярными диагоналями отрезки диагоналей образуют геометрическую прогрессию:

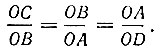
Доказательство. Пусть ABCD - прямоугольная трапеция, у которой 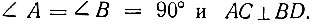В том случае докажем, что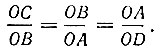

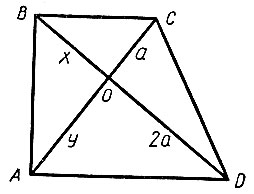
Рис. 3

Из того, что 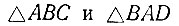прямоугольные, а OB и OA соответственно их высоты, вытекает:

и

Из (1) и (2), как следствие, получаем:

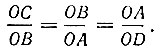
Что и требовалось доказать.

Пусть теперь требуется построить x так, чтобы 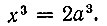где a - ребро данного куба, а x - ребро удвоенного куба. Для этого в полученной прогрессии достаточно положить OC = a, OB = x, OA = y, OD = 2a. Тогда будем иметь:

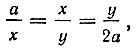
откуда

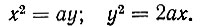
Путем несложных вычислений получается 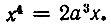Таким образом,

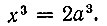
Следовательно, x = OB и будет ребром удвоенного куба.

Основываясь на доказанной лемме, само построение отрезка OB можно выполнить при помощи двух прямоугольных плотничьих наугольников. Это делается следующим образом. Берутся две взаимно перпендикулярные прямые m и n, пересекающиеся в точке O (рис. 4). На прямой m вправо от точки O отложим отрезок OC = a, где a - сторона куба, подлежащего удвоению.

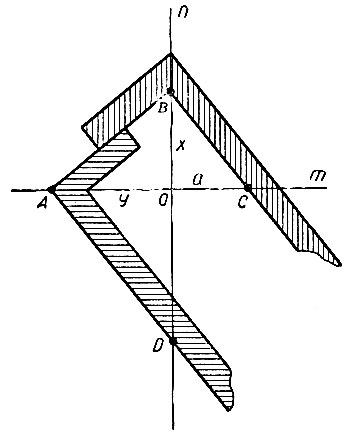
Рис. 4

На прямой я вниз от точки О отложим отрезок OD = 2a. Теперь берем два прямоугольных плотничьих наугольника (на рисунке они заштрихованы) и располагаем их так, как показано на рисунке, т. е.

1. чтобы катет первого наугольника проходил через точку C, которая считается данной, а вершина его находилась на прямой n;
2. чтобы катет второго наугольника проходил через точку D, которая считается также данной, а вершина находилась бы на прямой m;
3. остальные два катета того и другого наугольника должны соприкасаться.

При таком расположении двух наугольников по данным точкам C и D найдем на прямых тип точки A и B.

Тогда OB = x, а OA = y. По лемме

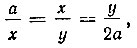
откуда

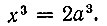
Следовательно, x = OB и есть построенное ребро удвоенного куба, что и нужно было сделать.

По свидетельству Эратосфена, Платон даже предложил механизм для выполнения решения делосской задачи, устройство и применение которого видно из чертежа (рис. 5). Один из наугольников, имеющих П-образную форму, с помощью специально устроенных пазов может скользить вдоль другого.

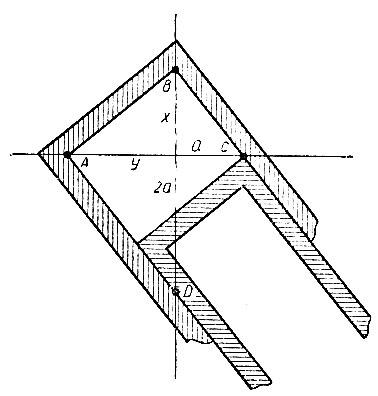
Рис. 5

Необходимо заметить, что хотя Платон и сконструировал прибор для механического решения делосской задачи, однако такие приборы он осуждал самым решительным образом. Вот, что пишет Плутарх в своей восьмой книге "Застольных бесед": "Сам Платон порицал друзей Евдокса, Архита и Менехма, которые хотели свести удвоение куба к механическим построениям, ибо они думали получить две средние пропорциональные не из теоретических соображений; но ведь таким образом уничтожается и гибнет благо геометрии, и этим путем геометрия возвращается обратно к чувственному, вместо того, чтобы подыматься выше этого и твердо держаться вечных, нематериальных образов". (См. Ван дер Варден, Пробуждающаяся наука, ГИФМЛ, М., 1959, стр. 224.)

Таким образом, Платон был против применения механических приборов, так как они, по его мнению, "отвращают" внимание ученых от чистой науки к материальному, от геометрических образов к негеометрическим. Он против "материальных вещей, которые требуют длительной обработки недостойным ремеслом" (Ван дер Варден, стр. 224). Вот почему многие историки математики склонны считать, что рассмотренное выше решение, приписываемое Платону, на самом деле Платону и не принадлежит. С этим согласен и упомянутый выше голландский математик Ван дер Варден. "Настоящий Платон, - по его словам,- не стал бы искать такого решения"(Ван дер Варден, стр. 225).

А если Платон и предложил "механическое решение", то предложил его как образец того, как не надо делать. Ван дер Варден полагает, что, возражая Архиту, Евдоксу и Менехму, Платон, по-видимому, вкладывал в свои слова такой смысл: "Вы нашли механические решения? В этом нет никакого искусства; даже и я, совсем не геометр, могу это сделать: для этого нужен только схематический чертеж, даже нет надобности в предварительном геометрическом решении задачи. Вот, взгляни... Но если поступать так, то все благо совершенно разрушается, так как внимание от чистой геометрии отвращается к материальным предметам..." (Ван дер Варден, стр. 226).

Решение Платона делосской задачи "механическим путем", несмотря на отрицательное отношение к нему самого изобретателя, является весьма оригинальным и простым в употреблении.