2. Решение Архита Тарентского

Гиппократ Хиосский, как известно, задачу об удвоении куба со стороной a свел к нахождению двух "вставок" x и y так, чтобы выполнялась геометрическая прогрессия: a, x, y, 2a, т. е. чтобы 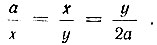Эти "вставки" геометрическим путем (при помощи циркуля и линейки) найти нельзя, так как это равносильно геометрическому построению 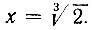Стало быть, эти "вставки" нужно искать "не-геометрическим" построением.

Заслуга Архита Тарентского (ок. 440- 360 гг. до н. э.) как раз и заключается в открытии такого построения. Задачу об удвоении куба он решил весьма оригинальным стереометрическим построением, основанным на рассмотрении пересечения нескольких поверхностей вращения.

Архит Тарентский несомненно является одним из выдающихся, если не самым выдающимся, геометров своего времени. Как полагают, он был учеником пифагорейца Филолая и близким другом Платона, которого он спас от рабского плена. Он был учителем знаменитого Евдокса, создавшего теорию пропорций. В своем родном городе Таренте он семь раз избирался стратегом. Как полководец, Архит не проиграл ни одного сражения и поэтому снискал у своих сограждан большой авторитет и славу.

Круг научных интересов Архита весьма разнообразен. Вот далеко не полный список его открытий:

1. Развил арифметику натуральных чисел.
2. Далеко продвинул теорию несоизмеримых величин.
3. Дал теоретико-числовое обоснование теории музыки (по словам Птолемея, его можно считать самым крупным античным теоретиком музыки).
4. Первый из античных ученых дал систематическую разработку механики на математических основах.
5. Писал сочинения о машинах и пытался сам конструировать их. Это он, любя детей, сконструировал в подарок им механического деревянного голубя, который мог летать.

Но самым блестящим достижением Архита как геометра является, конечно, решение знаменитой делосской задачи, в котором проявился его необыкновенно тонкий ум и весьма большой талант. Решение делосской задачи, выполненное Архитом, вызывает восторг и удивление даже у современных математиков. Так, например, крупный голландский математик Ван дер Варден (род. 1903), известный своими трудами по современной алгебре и замечательными исследованиями по истории античной математики, излагая метод Архита, которым он решил задачу об удвоении куба, не мог воздержаться от восклицания: "Разве это не замечательно? Архита, должно быть, осенило некоторое поистине божественное вдохновение, когда он нашел это построение" (Б. Л. Ван дер Варден, Пробуждающаяся наука, ГИФМЛ, М., 1959, стр. 210).

В чем же суть столь замечательного построения Архита, с помощью которого решается одна из замечательных задач древности? Это построение приводится в комментариях Евтокия, которое он позаимствовал у Евдема. Воспроизводим это построение, изменив несколько стиль изложения и исключив некоторые излишние повторения.

Пусть AD и G - два отрезка и требуется найти два средних пропорциональных между ними. На большом отрезке AD, как на диаметре, опишем круг ABDZ и отложим хорду AB = G, которая, будучи продолжена, с проведенной в D касательной к кругу пересечется в точке P (рис.2). Проведем прямую BEZ параллельно PDO. Далее, на полукруге ABD построим прямой полуцилиндр, а на отрезке AD, как на диаметре,- полукруг (на рисунке он не показан), перпендикулярный кругу ABDZ. Этот полукруг будем называть "первым вертикальным полукругом". Если теперь будем вращать этот первый вертикальный полукруг от точки D к точке D₁, оставляя его все время вертикальным, вокруг образующей полуцилиндра, проходящей через точку A, считая эту точку неподвижной, то полукруг на указанном выше прямом полуцилиндре высечет некоторую кривую линию.

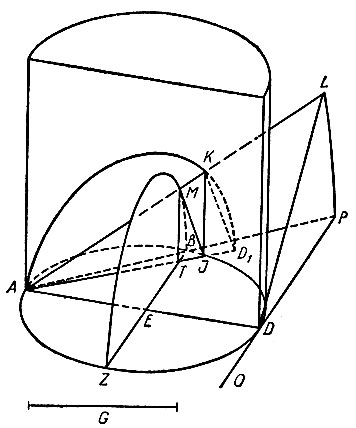
Рис. 2

При вращении 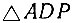около AD от точки P к точке L прямая AP опишет некоторый полуконус, причем точка B опишет полукруг BMZ, который будем называть "вторым вертикальным полукругом". Этот полуконус своей образующей AL пересечет полученную кривую на полуцилиндре в точке K, принадлежащей образующей IK. Пусть прямая, соединяющая I с A, пересечет BZ в точке T, а прямая AL (образующая полуконуса) пересечет "второй вертикальный полукруг" BMZ в точке M. Проведем также прямые KD₁, MI и MT. Поскольку вертикальные полукруги AKD₁ и BMZ расположены перпендикулярно к горизонтальному кругу ABDZ, то линия их пересечения MT будет перпендикулярна к тому же горизонтальному кругу ABDZ. Таким образом,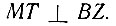

По теореме о перпендикуляре, опущенном из точки окружности на диаметр, будем иметь:

Далее, по свойству хорд, проходящих через точку внутри круга ABDZ, получим:

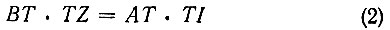
Из (1) и (2) вытекает

Из (3) следует, что угол AMI - прямой. Угол AKD₁ - также прямой, так как он вписан в полуокружность AKD₁ и опирается на диаметр AD₁. Следовательно, 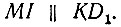Выходит, что 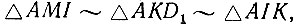откуда

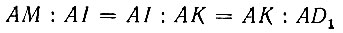
Но 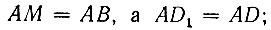получим:

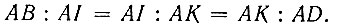
Если данные отрезки AB и AD соответственно положить равными a и 2a, где a - ребро данного куба, а отрезки AI и AK обозначить соответственно через x и y, то окончательно получим:

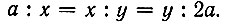
Таким образом, для двух заданных отрезков a и 2a найдены два средних пропорциональных x и y, следовательно, x = AI и будет ребром удвоенного куба. Знаменитая делосская задача об удвоении куба решена.