§ 4. Решение задачи об удвоении куба при помощи вспомогательных средств

1. Решение Гиппократа Хиосского при помощи "вставок"

Одним из первых древнегреческих геометров, сделавшим значительный шаг в решении задачи об удвоении куба, был Гиппократ Хиосский (5 в. до н. э.). (Не надо смешивать с Гиппократом - врачом, основоположником античной медицины, родом из города Меропис находящегося на острове Кос.)

Гиппократ Хиосский был знаменитым геометром своего времени. Жил около 440 г. до н. э. Он является автором первого систематического сочинения по геометрии, которое, к сожалению, до нас не дошло.

Аристотель характеризует Гиппократа Хиосского как изобретательного геометра, но мало приспособленного к обыденной жизни человека. Начав жизнь свою богатым купцом, он скоро по своей чрезмерной доверчивости и наивности был самым бессовестным образом обманут сборщиками налогов в Византии, которые своими плутовскими проделками лишили его всего денежного состояния.

Решение стереометрической задачи, каковой является делосская задача об удвоении куба, Гиппократ Хиосский свел к рассмотрению планиметрической задачи, заключающейся в нахождении двух средних пропорциональных между двумя данными отрезками, из которых второй в два раза больше первого, т. е. к нахождению таких двух отрезков x и y, которые, будучи "вставлены" между двумя данными a и 2a, составили бы вместе с ними геометрическую прогрессию: a, x, y, 2a.

Поскольку a, x, y, 2a - геометрическая прогрессия, то 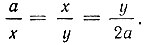Откуда 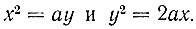Следовательно,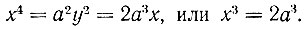

Выходит, что c и есть ребро искомого куба, превосходящего по объему данный куб с ребром a в два раза.

Однако, как и следовало ожидать, Гиппократу не удалось отыскать ребро удвоенного куба x с помощью геометрического построения, прибегая только к циркулю и линейке, но ему вполне удалось, как мы убедились выше, стереометрическую задачу свести к плоской задаче на отыскание двух "вставок" x и y между a и 2a, причем a - ребро данного куба, а x - искомое ребро удвоенного куба.