§ 3. О доказательстве невозможности решить задачу об удвоении куба при помощи циркуля и линейки

Чтобы иметь хотя бы некоторое представление о разрешимости и неразрешимости задач на построение, ограничимся следующим небольшим замечанием. Прежде всего напомним (это учащиеся знают хорошо), что при помощи циркуля и линейки можно сравнительно легко построить выражения:

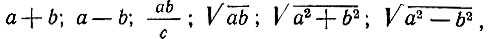
где a, b, c суть данные или найденные отрезки. Если решение задачи сводится к последовательному выполнению этих операций в конечном числе, то задача оказывается разрешимой при помощи циркуля и линейки^*. Если же решение некоторой задачи не сводится к последовательному выполнению указанных выше операций в конечном числе, то такую задачу при помощи циркуля и линейки решить невозможно. Задача об удвоении куба и является примером таких неразрешимых задач, которую нельзя решить, прибегая только к циркулю и линейке, т. е. путем проведения окружностей и прямых линий.

^* (Пользуясь указанными выше операциями на построение, можно дать правила, позволяющие построить без вычислений резки, длины которых в точности равны действительным корням квадратных уравнений 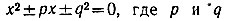где p и q рассматриваются к длины некоторых отрезков, м. по этому поводу: Б. И. Аргунов и М. Б. Балк, Геометрические построения на плоскости, Учпедгиз, М., 1955, стр. 181-185).)

Современными средствами, выходящими за пределы школьного курса математики, строго доказано, что кубическое уравнение с рациональными коэффициентами, не имеющее рациональных корней, не может быть разрешимо в квадратных радикалах, т. е. ни один из корней этого уравнения не может быть построен при помощи циркуля и линейки. В дальнейшем эту теорему будем называть "теоремой неразрешимости". Доказательство этой теоремы можно прочитать, например, в книге Б. И. Аргунова и М. Б. Балка, "Геометрические построения на плоскости" (стр. 214-217).

В предыдущем параграфе было показано, что задача об удвоении куба сводится к решению кубического уравнения

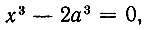
где a есть ребро данного куба, x - искомое ребро удвоенного куба.

Приняв для простоты длину ребра данного куба за 1, получим уравнение:

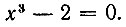
Это уравнение с рациональными коэффициентами, как легко убедиться, не может иметь рациональных корней. Следовательно, по "теореме неразрешимости", задача об удвоении куба не может быть решена при помощи циркуля и линейки.

Первый из ученых, кто открыто высказал мнение, что точное построение отрезка, равного 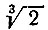, посредством циркуля и линейки неосуществимо, был знаменитый французский ученый Р. Декарт (1596-1650 гг.). В 1637 г. он высказал предположение, что вообще кубический корень из некубического рационального числа есть иррациональность, не приводящаяся к конечному числу действий извлечения квадратного корня.

Р. Декарт

Строгое доказательство неразрешимости задачи об удвоении куба при помощи циркуля и линейки было дано французским математиком П. Ванцелем в 1837 г.