§ 2. Попытка решить задачу об удвоении куба при помощи циркуля и линейки

Древние греки сравнительно легко решили задачу об удвоении квадрата. Для этого надо было уметь строить при помощи циркуля и линейки корень квадратный из двух. Действительно, если сторона данного квадрата равняется a, а сторона искомого квадрата х, то, согласно условию задачи, будем иметь:

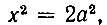
откуда

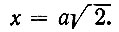
Чтобы построить нужно построить гипотенузу равнобедренного прямоугольного треугольника, у которого каждый катет равен единице. Теперь остается отрезок, равный √2, увеличить в а раз, тогда и получим сторону искомого квадрата. А проще всего в качестве x взять диагональ данного квадрата, которая, по теореме Пифагора, как раз и будет равняться a√2 (рис. 1).

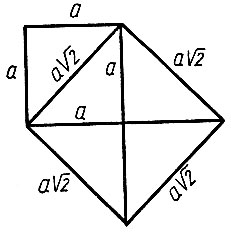
Рис. 1

Обобщая задачу об удвоении квадрата, древние греки перешли к рассмотрению задачи об удвоении куба и также стремились решить ее при помощи циркуля и линейки. Оказалось, что решение задачи об удвоении куба сводится к геометрическому построению корня кубического из двух. Действительно, если ребро данного куба положить равным a, а ребро искомого куба - x, то, согласно условию задачи, будем иметь:

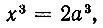
откуда

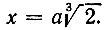
Однако все старания построить 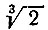циркулем и линейкой не увенчались успехом. И трудно сказать, как долго еще продолжались бы эти попытки, если бы, наконец, в первой половине XIX в. не было доказано, что при помощи циркуля и линейки, без привлечения других вспомогательных средств, 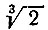построить нельзя.