4. Решение Менехма

Дальнейший значительный вклад в решение делосской задачи внес знаменитый ученый древности Менехм, живший в IV в. до н. э. Он был учеником знаменитого Евдокса и прославился работами по астрономии и математике. Менехм был смелого и независимого характера. Об этом свидетельствует следующий диалог, происшедший якобы между Александром Великим и Менехмом.

Александр Великий (обращаясь к Менехму):

- Я хочу изучить всю премудрость геометрической науки, так скажи мне: нет ли для нас, царей, более короткого пути к геометрии?

Менехм (с достоинством):

- О царь, для путешествующих по этой стране есть царские дороги и дороги для простых граждан, но в геометрии для всех одна дорога!..^*

^* (Этот же диалог приписывается и Евклиду (составителю знаменитых "Начал") с царем Птолемеем. Все же первоначальная редакция, по-видимому, относилась к Менехму.)

Изучение конуса привело Менехма к весьма замечательному открытию, а именно к открытию так называемых "конических сечений". А глубокое размышление над свойствами конических сечений и над делосской задачей явилось источником другого крупнейшего открытия, заключающегося в применении конических сечений к решению задачи об удвоении куба.

Что это за конические сечения? Коническими сечениями называются кривые, получаемые путем пересечения конуса секущей плоскостью.

Сам Менехм рассматривал исключительно конус вращения. Конусы вращения в зависимости от величины угла при вершине (угла, составленного двумя образующими, расположенными в плоскости осевого сечения) он делил на три категории: прямоугольные, когда угол при вершине прямой, тупоугольные, когда угол при вершине тупой, и остроугольные, когда угол при вершине острый. Для получения конических сечений секущая плоскость бралась перпендикулярно к образующей (рис. 6).

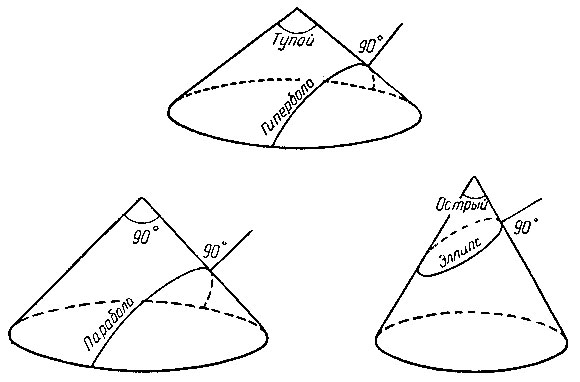
Рис. 6

Коническое сечение прямоугольного конуса дает параболу, коническое сечение тупоугольного конуса - гиперболу и коническое сечение остроугольного конуса - эллипс.

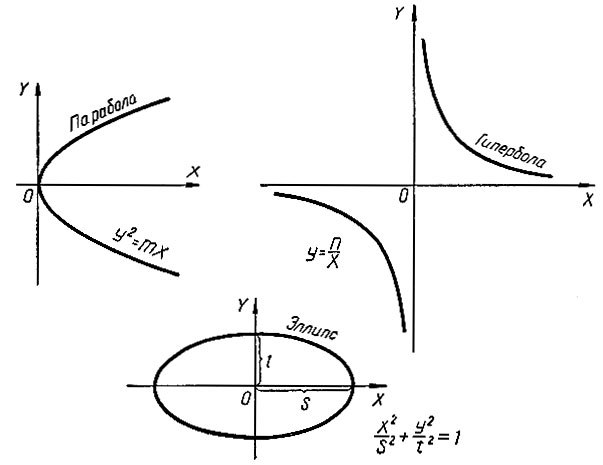
Рис. 7

Эти кривые, отнесенные к осям координат, введенным впервые французским математиком Р. Декартом в XVII в., имеют вид (рис. 7). Их уравнения будут:

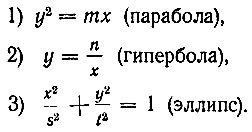
Задачу об удвоении куба Менехм решает двумя способами.

Первый способ. Решение задачи об удвоении куба с ребром а сводится к рассмотрению двух парабол:

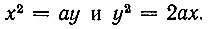
Решая эти уравнения, как систему, относительно x, будем иметь

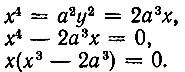
Получаем два вещественных корня 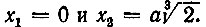Первый корень не удовлетворяет условию задачи. Следовательно, искомым решением будет второй корень, т. е. ребро удвоенного куба равняется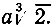

Путем построения графиков обеих парабол искомое ребро удвоенного куба получается, как ненулевая абсцисса точки пересечения парабол (рис. 8).

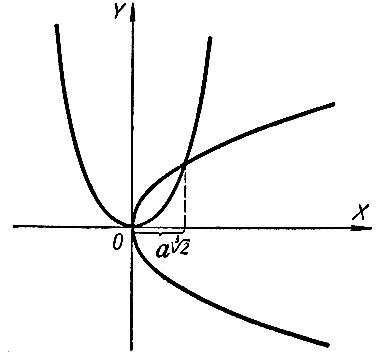
Рис. 8

Второй способ. Задача об удвоении куба сводится к решению двух уравнений, из которых одно - уравнение гиперболы, а другое - уравнение параболы:

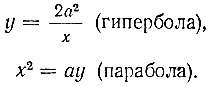
Решая совместно относительно x, получим:

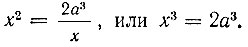
Следовательно,

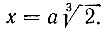
Путем построения графиков искомое ребро удвоенного куба находится, как абсцисса пересечения гиперболы с параболой (рис. 9).

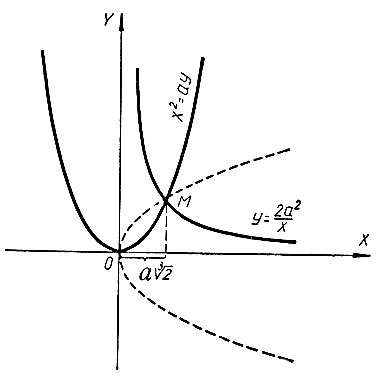
Рис. 9

Необходимо заметить, что в последнем случае вместо параболы 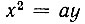можно взять параболу 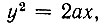которая на чертеже изображена пунктиром^*.

^* (Уместно добавить, что идею графического решения задачи об удвоении куба можно осуществить бесконечным множеством способов, среди которых, конечно, заслуживают внимания наиболее "простые" кривые, которые и применял для этой цели Менехм.)