5. Решение Эратосфена при помощи сконструированного им прибора "мезолябия"

К тому, что говорилось выше об Эратосфене в связи с происхождением делосской задачи, добавим, что Эратосфен родился в Кирене, образование получил в Александрии и Афинах. Когда ему было около 50 лет, его пригласили ко двору Птолемея III в качестве воспитателя наследника престола и быть главой всемирно известной Александрийской библиотеки. В области математики Эратосфен предложил весьма эффективный способ нахождения ряда простых чисел ("эратосфеново решето") и занимался изучением средних величин.

Имя Эратосфена тесно связано с историей делосской задачи. Он построил оригинальный и весьма простой прибор для механического решения задачи об удвоении куба. Этот прибор носит название "мезолябия", что в переводе означает "уловитель", т. е. уловитель двух средних величин, из которых одна и составляет искомую сторону удвоенного куба.

Мезолябий Эратосфена состоит из двух параллельно расположенных реек m и n, расстояние между которыми равно удвоенной стороне данного куба, т. е. 2a. К этим рейкам прикреплены три равных прямоугольных треугольника, из которых один, самый левый, смонтирован неподвижно, а другие два могут перемещаться вдоль пазов, устроенных в рейках, причем на верхнюю рейку опираются равные катеты, а на нижнюю - их противоположные вершины (рис. 10).

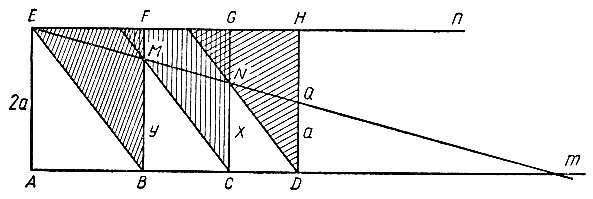
Рис. 10

На катете HD самого правого подвижного треугольника откладываем отрезок DQ = a. Теперь двигаем подвижные треугольники с таким расчетом, чтобы точки пересечения катета одного треугольника с гипотенузой следующего за ним (M и N) располагались бы на одной прямой с E и Q. Тогда из рассмотрения соответствующих подобных треугольников получаем:

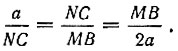
Обозначая NC через x и MB через y, будем иметь:

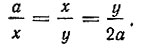
Следовательно, x = NC и будет найденной величиной искомого ребра удвоенного куба. Делосская задача решена.

Текст механического решения Эратосфена был высечен на камне в храме царя Птолемея в Александрии. Над текстом находилась бронзовая модель, состоящая из трех треугольников, которые можно было передвигать взад и вперед между двумя рейками.

На мраморной доске в этом же храме были высечены также стихи Эратосфена. Стихи эти таковы:

"Если бы, друг, ты замыслил большое из малого сделать, 
Куб сотворить ли двойной, иль перестроить объем, 
Это возможно - и сени расширишь, и яму просторней 
Выроешь, и водоем влагой наполнишь двойной. 
Вот мой прибор: меж линеек две средние сразу отыщешь, 
Между краями других ты их отметишь концы. 
Нужды тебе уж не будет в премудром цилиндре Архита, 
В конусе не для тебя высек триаду Менехм, 
И с богоравным Евдоксом изогнутых линий не надо, 
Циркулем вооружась, тонкий изгиб находить. 
Сдвинув отважно линейки, легко мириады построишь 
Средних желанных твоих, с меньшей из данных начав. 
Счастлив ты, царь Птолемей,- ты дал вечному сыну 
Вечно блаженному дар сладкий для муз и царей. 
Зевс, бог вселенной! В грядущем пусть с милостью той же 
                                              он примет 
Скипетр от царской руки - и да свершится сие. 
Тот же, кто жертву во храме великом увидит, да скажет: 
- Дар этот Эратосфен людям, измыслив, принес."

В приведенных стихах Эратосфена упоминаются решения Архита, Менехма и Евдокса. С решениями Архита и Менехма мы ознакомились выше, а решение Евдокса до нас, к сожалению, не дошло (считается утерянным).