
6. Решение Буонафальче (приближенное решение)
Буонафальче дает одно из самых простых приближенных решений задачи об удвоении куба при помощи циркуля и линейки (точного решения этой задачи при помощи циркуля и линейки, как известно, дать нельзя).
Пусть дан куб с ребром a и требуется найти ребро x удвоенного куба, т. е. чтобы для x выполнялось равенство 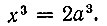 Решение выполним приближенно при помощи только циркуля и линейки. Пользуясь циркулем и линейкой, строим прямоугольный равнобедренный треугольник ABC с боковой стороной, равной а (рис. 11). Теперь сторону
Решение выполним приближенно при помощи только циркуля и линейки. Пользуясь циркулем и линейкой, строим прямоугольный равнобедренный треугольник ABC с боковой стороной, равной а (рис. 11). Теперь сторону 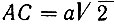 делим на шесть равных частей и находим на катете BC от точки C к точке B точку D с таким расчетом, чтобы выполнялось равенство
делим на шесть равных частей и находим на катете BC от точки C к точке B точку D с таким расчетом, чтобы выполнялось равенство 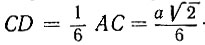
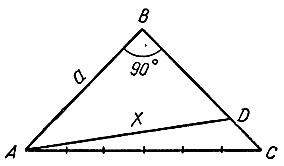
Рис. 11
Соединив A с D, получим отрезок AD, который для краткости обозначим через x. Теперь подсчитаем, чему равняется x.
По теореме Пифагора будем иметь:
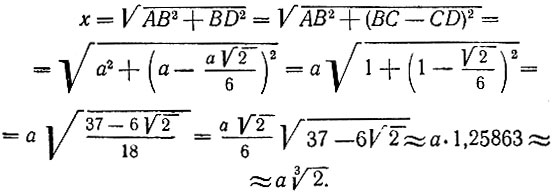
Итак, 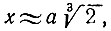 где
где 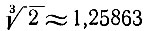 (на самом деле
(на самом деле 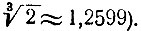
Следовательно, ребро удвоенного куба приблизительно равно 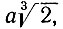 если ребро данного куба равно a. Таким образом, если данный куб имеет ребро a, равное отрезку AB, то x - искомое ребро удвоенного куба - будет приблизительно равняться отрезку AD, который отличается от истинного значения искомого ребра меньше, чем на
если ребро данного куба равно a. Таким образом, если данный куб имеет ребро a, равное отрезку AB, то x - искомое ребро удвоенного куба - будет приблизительно равняться отрезку AD, который отличается от истинного значения искомого ребра меньше, чем на 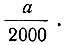
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'