
§ 6. Обобщенное решение задачи оптимального управления методом динамического программирования
Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов, причем каждый раз оптимизируется управление только на одном шаге, однако таким образом, чтобы добиться оптимизации всей операции по выбранным критериям. Таким образом, если независимо от характера решаемой задачи ее удается представить в виде многошагового процесса, то решение такой задачи может быть получено методом динамического программирования. Поэтому в класс задач, решаемых этим методом, включаются не только задачи экономического характера, но также множество задач, имеющих самых различные приложения. Для примера можно привести задачу о замене оборудования промышленного предприятия и задачу о рациональной загрузке корабля, задачу о выборе наискорейшего (наивыгоднейшего) пути и родственную ей задачу об оптимальной траектории полета самолета или ракеты и т. д. Многочисленные приложения находит динамическое программирование в оптимизации проектирования крупных изделий (паровых турбин, многоступенчатых ракет и др.) и в планировании военных операций. При таком разнообразии решаемых задач естественно, что и критерии оптимизации носят самый различный характер и могут выбираться самыми различными способами. Причем одна и та же задача при оптимизации по разным критериям может иметь различные решения.
Поэтому чтобы отвлечься от конкретного содержания задачи и характера критерия оптимизации, обычно говорят [10-14] о поведении некоторой физической системы S, состояние которой может с течением времени меняться. Предполагается, что этот процесс изменения является управляемым, т. е. мы имеем возможность влиять на его ход, выбирая необходимое в данном случае управление, которое обозначим через U. Величина выбранного критерия W оказывается зависящей от примененного управления W = = W (U), и требуется выбрать такое управление U, чтобы в конце процесса величина W получилась оптимальной (максимальной или минимальной):
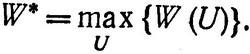
(3.33)
Для системы S должны быть учтены условия, накладываемые на ее начальное состояние S0 и конечное состояние Sn. Оба состояния S0 и Sn могут быть либо заданы точно в виде числа, пункта назначения и т. д., или в общем случае могут быть указаны только области начальных 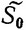 и конечных
и конечных 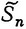 состояний. Требование того, что состояния S0 и Sn принадлежали соответствующим областям, записывается с помощью принятого в математике знака включения
состояний. Требование того, что состояния S0 и Sn принадлежали соответствующим областям, записывается с помощью принятого в математике знака включения
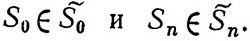
В обобщенной постановке задача оптимального управления окончательно формулируется следующим образом: из множества возможных управлений U выбрать оптимальное управление U*, которое переводит физическую систему S из начального состояния S0∈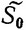 в конечное состояние Sn∈
в конечное состояние Sn∈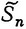 таким образом, чтобы выбранный критерий W (U) обращался в максимум (минимум) W*.
таким образом, чтобы выбранный критерий W (U) обращался в максимум (минимум) W*.
Для наглядности полезно дать процессу управления геометрическую интерпретацию. Для этого нам потребуется использовать представление о так называемом фазовом пространстве.
Обычно состояние каждой физической системы можно описать посредством некоторого количества различных параметров (переменных), например, координат и скоростей физического тела, количества наличных средств или товаров, численных параметров, характеризующих качество узлов, применяемых при проектировании определенного изделия, и т. д. Используем эти параметры в качестве координат фазового пространства и соответственно будем называть эти параметры фазовыми координатами системы. Если в качестве фазовых координат в задаче используются обычные пространственные координаты, то понятие фазового пространства совпадает с понятием обычного пространства. В большинстве же случаев фазовое пространство является чисто условным понятием, используемым для наглядной геометрической интерпретации изменения состояния системы S в процессе управления. Это изменение состояния будет изображаться как перемещение точки S, описывающей состояние системы в данный момент, в фазовом пространстве, характеризующем данную систему S. Выбор какого-либо управления U означает выбор соответствующего закона движения точки S, траектории ее движения в фазовом пространстве.
Если состояние системы характеризуется не более чем тремя параметрами xj, то фазовое пространство можно условно изобразить в виде соответствующего обыкновенного пространства одного, двух или трех измерений. В этом случае область возможных состояний системы можно изобразить в виде некоторой геометрической области, а управляемый процесс будет интерпретироваться как перемещение точки 5 из начальной области 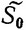 в конечную
в конечную 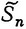 по некоторой траектории. Примеры фазового пространства будут даны ниже.
по некоторой траектории. Примеры фазового пространства будут даны ниже.
Если число параметров, характеризующих состояние системы, более трех, то наглядная геометрическая интерпретация оказывается невозможной, однако геометрическая терминология оказывается удобной: изменение состояния системы можно описывать как перемещение точки в n-мерном пространстве по некоторой траектории. Впрочем, как показано выше, задачи с числом переменных управления более трех лишь в редких случаях могут быть решены методом динамического программирования из-за быстрого увеличения вычислительных трудностей с ростом числа переменных.
Используя понятие фазового пространства, задачу оптимального управления можно сформулировать еще и следующим образом: из множества возможных управлений U выбрать оптимальное управление U*, которое переводит точку S фазового пространства из начальной области 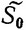 в конечную область
в конечную область 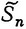 таким образом, чтобы выбранный критерий W обращался в максимум (минимум) W*.
таким образом, чтобы выбранный критерий W обращался в максимум (минимум) W*.
Как уже отмечалось, природа используемого критерия тесным образом связана с характером решаемой задачи. Например, это может быть и доход от вложенных средств или время, затраченное на преодоление заданного расстояния, объем выпущенной продукции или коэффициент полезного действия вновь проектируемой установки и т. д. Однако при всем разнообразии конкретного выражения критерия оптимального управления в условиях многошагового процесса структура критерия не отличается таким разнообразием. В рассмотренных выше задачах распределения критерий обладал тем свойством, что его полное значение в течение всего процесса получалось простым суммированием частных значений wj того же критерия, полученных на отдельных шагах, т. е. критерий обладал тем свойством, что
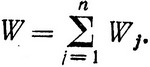
(3.34)
Критерий такого вида называется аддитивным.
Для большого числа задач, решаемых методом динамического программирования, характерно именно наличие аддитивного критерия. Более того, если в первоначальной постановке задачи критерий оказывается неаддитивным, то по возможности стараются так видоизменить постановку задачи или критерий, чтобы добиться аддитивности последнего.
В некоторых случаях такое видоизменение критерия оказывается весьма несложным. В частности, если критерий является "мультипликативным", т. е. если он представляет собой произведение частных значений того же критерия, получаемых на отдельных шагах
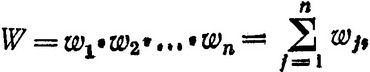
(3.35)
то путем логарифмирования выражения (3.35) его можно преобразовать к аддитивному:
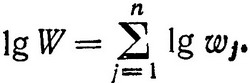
(3.36)
В процессе решения задачи теперь следует искать максимум самой величины W, а ее логарифма.
Покажем, как найти обобщенное решение задачи оптимального управления с аддитивным критерием методом динамического программирования.
Пусть весь процесс движения системы из состояния 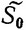 состояние
состояние 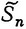 разбит на n шагов и на каждом j-м шаге применяется управление Uj, посредством которого система из состояния Sj-1 переводится в состояние Sj. Ясно, что новое состояние зависит от того, каково было предыдущее состояние Sj-1 и какое управление Uj использовалось, т. е.
разбит на n шагов и на каждом j-м шаге применяется управление Uj, посредством которого система из состояния Sj-1 переводится в состояние Sj. Ясно, что новое состояние зависит от того, каково было предыдущее состояние Sj-1 и какое управление Uj использовалось, т. е.
Sj = Sj(Sj-1, Uj).(3.37)
Пусть при переходе системы из состояния Sj-1 в Sj ветчина изменения критерия (выигрыш) также зависит от
wj = wj(Sj-1, Uj).(3.38)
В результате всего процесса за n шагов получаем полное изменение критерия (полный выигрыш):
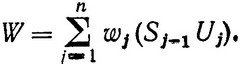
(3.39)
Введем также следующие обозначения:

Очевидно, что эти величины есть не что иное, как
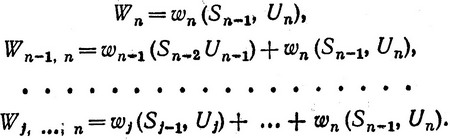
(3.40)
Как мы уже знаем, процесс решения задачи методом динамического программирования начинается с последнего n-го шага. Допустим, после (n-1)-го шага система находится в состоянии Sn-1, и это состояние нам известно.
Обозначим через U*n (Sn-1) оптимальное управление на n-м шаге, которое обеспечивает, во-первых, переход системы в состояние Sn∈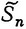 и, во-вторых, получение максимального выигрыша на последнем шаге:
и, во-вторых, получение максимального выигрыша на последнем шаге:
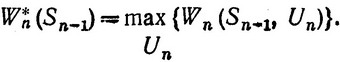
(3.41)
Поскольку состояние Sn-1 в действительности нам неизвестно и мы лишь условились о том, что оно нам известно, управление U* (Sn-1) является лишь условным оптимальным управлением, зависящим от состояния Sn-1. Соответственно и максимальный выигрыш W*n (Sn-1) также является условным выигрышем. Соответствие между этими величинами запишем в виде
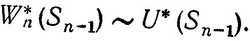
Оптимизацию последнего шага следует провести для всех возможных состояний системы, из которых за один шаг можно перейти в конечное состояние 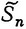 . Таким образом, для каждого состояния мы находим условное оптимальное управление, или, другими словами, в каком бы состоянии ни оказалась система после (n-1)-го шага, мы уже знаем, как нам поступать дальше.
. Таким образом, для каждого состояния мы находим условное оптимальное управление, или, другими словами, в каком бы состоянии ни оказалась система после (n-1)-го шага, мы уже знаем, как нам поступать дальше.
Аналогично производим оптимизацию предпоследнего (n-1)-го шага. В результате примененного управления на этом шаге также получим выигрыш, зависящий как от состояния системы Sn-2, так и от примененного управления:
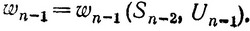
(3.42)
При этом система перейдет в состояние Sn-1, которое зависит от предыдущего состояния и примененного управления
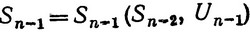
(3.43)
поэтому можно написать:
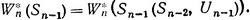
(3.44)
Здесь и далее согласно общепринятому правилу для выражения сложной функциональной зависимости используются только круглые скобки.
Полный выигрыш на двух последних шагах при оптимальном управлении на последнем n-м шаге и произвольном управлении на (n-1)-м шаге согласно (3.42) и (3.43), очевидно, составляет:
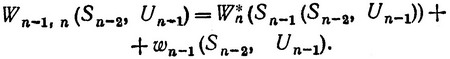
(3.45)
Для того чтобы оптимизировать выигрыш на n-м и (n-1)-м шагах, выбираем такое условное оптимальное управление U*n-1 (Sn-2), при котором согласно принципу оптимальности достигается максимум величины (3.45):
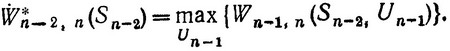
(3.46)
Конечно, в качестве возможных исходных состояний Sn-1 можно брать лишь такие состояния, из которых за два шага можно попасть в область 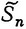 . Как и раньше, используем символическую запись, показывающую связь условного максимального выигрыша и условного оптимального управления на (n-1)-м шаге:
. Как и раньше, используем символическую запись, показывающую связь условного максимального выигрыша и условного оптимального управления на (n-1)-м шаге:
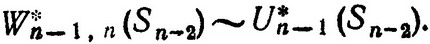
На этом заканчивается оптимизация процесса на двух последних шагах: (n-1)-м и n-м и можно переходить к оптимизации (n-2)-го и т. д. шагов. Поступая точно таким же образом, как в случае (n-1)-го шага, можно найти условные максимальные выигрыши и соответствующие им условные оптимальные управления на более ранних шагах:
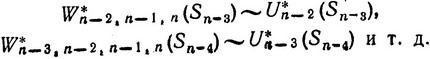
Если же оптимизирован (j+1)-й шаг для любого возможного исхода j-го шага, т. е. известны
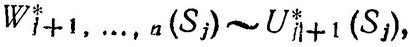
то условная оптимизация j-го шага производится по общей формуле:
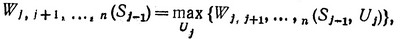
(3.47)
где
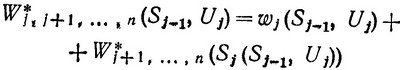
(3.48)
(сравним (3.47) с (3.46) и (3.48) с (3.45)).
Формула (3.47) определяет условный максимальный выигрыш на последних шагах, начиная с j-го, и соответствующее условное оптимальное управление на j-м шаге:
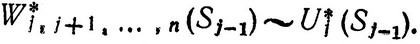
Применяя последовательно шаг за шагом описанную процедуру вплоть до первого шага, получаем, наконец, условный максимальный выигрыш и соответствующее условное управление:
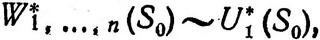
где S0∈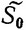 . Если область
. Если область 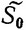 представляет собой лишь одну точку в фазовом пространстве, то выбора S0 нет, и это начальное состояние есть оптимальное начальное состояние S*0, т. е. S0 = S0*. Если же точка S0 может произвольно выбираться в пределах области
представляет собой лишь одну точку в фазовом пространстве, то выбора S0 нет, и это начальное состояние есть оптимальное начальное состояние S*0, т. е. S0 = S0*. Если же точка S0 может произвольно выбираться в пределах области 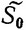 , то нужно выбрать начальное состояние таким образом, чтобы получить
, то нужно выбрать начальное состояние таким образом, чтобы получить
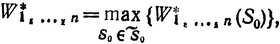
(3.49)
где максимум берется по всем состояниям S0 из области 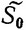 . Точка (или точки) S*0, где достигается этот максимум, является оптимальным начальным состоянием системы, а максимум W1, ..., n* - абсолютным максимумом (выигрышем) W*, получающимся в процессе перехода системы из области
. Точка (или точки) S*0, где достигается этот максимум, является оптимальным начальным состоянием системы, а максимум W1, ..., n* - абсолютным максимумом (выигрышем) W*, получающимся в процессе перехода системы из области 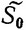 в область
в область 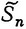 , т. е.
, т. е.
W* = W*1, ..., n∼S*0.
Для окончательного решения задачи остается только среди найденных условных оптимальных управлений найти настоящее оптимальное управление на всех n шагах. Чтобы это сделать, мы должны снова проделать весь n-шаговый процесс решения, только теперь от начала до конца, используя уже полученные результаты по условному оптимальному управлению.
Поскольку нам известно оптимальное начальное состояние S*0, то необходимое на первом шаге оптимальное управление будет
U1* = U1*(S*0).(3.50)
Под действием управления (3.50) система переходит в новое состояние, определяемое выражением
S1* = S1(S0*, U*1).
Второй шаг уже был оптимизирован нами для произвольного состояния системы после первого шага S1. Теперь же мы окончательно знаем состояние системы S*1 после первого шага и поэтому можем окончательно выбрать оптимальное управление на втором шаге:
U2* = U2*(S*1).(3.51)
Точно так же поступаем с третьим и всеми последующими шагами, пока не дойдем до оптимального управления на последнем шаге
Un* = Un*(S*n-1).(3.52)
и оптимального конечного состояния системы после n шагов
Sn* = Sn*(Sn-1*, U*n).
Этим завершается решение задачи. В результате всей процедуры находятся:
- оптимальное начальное состояние S*0∈
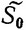 ,
,
- оптимальное управление на всех шагах (так называемый вектор оптимального управления) U* ≡ (U1*, U*2, ..., U*n),
- максимально возможное значение (3.49) критерия (выигрыша) W*,
- конечное состояние системы Sn*∈
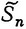 в которое она придет при оптимальном управлении U*.
в которое она придет при оптимальном управлении U*.
Таким образом, мы получили обобщенное решение задачи оптимального управления методом динамического программирования. Хорошей иллюстрацией использования такого метода является рассмотренное выше решение задачи распределения ресурсов. В следующих параграфах мы рассмотрим ряд различных практических задач и дополнительных приемов, облегчающих их решение. При этом общие идеи, сформулированные в данном параграфе, будут использоваться при решении всех этих задач.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'