
§ 7. Разновидности задачи распределение ресурсов [11]
Прежде всего для тог© чтобы продемонстрировать применимость метода динамического программирования также к задачам оптимизации, возникающих в областях, весьма далеких от области экономики, рассмотрим задачу о распределении веса между ступенями многоступенчатой ракеты.
Задача ставится следующим образом: ракета, имеющая n ступеней, должна поднимать полезную нагрузку в виде контейнера весом g и иметь стартовый вес, равный G + g, где G - собственный вес ракеты, т. е. вес оборудования, двигателей и топлива. Вес ракеты представляется в виде
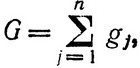
(3.53)
где gj - вес ее j-й ступени.
Приращение скорости, которое получает контейнер после отрабатывания и сбрасывания всех ступеней ракеты, есть
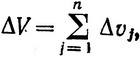
(3.54)
где Δvj - приращение скорости, которое получает ракета за время работы двигателя j-й ступени.
Известно, что Δvj выражается следующим образом:
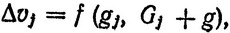
(3.55)
где Gj = gj+1 + gj+2 + ... + gn - полный собственный вес ракеты, оставшийся ко времени сбрасывания j-й ступени (резервированный вес). Этот вес, очевидно, также равен
Gj = G - g1 - g2 - ... - gj.
"Требуется распределить вес G между n ступенями ракеты таким образом, чтобы приращение скорости ΔV получилось максимальным.
Рассмотрим сначала процесс решения в общем виде, к обычно, начинаем решать задачу с конца. Последняя ступень, очевидно, должна иметь вес, который дополнит вес всех остальных ступеней Gn-1 до заданного веса сеты G. Поэтому условное оптимальное управление на последнем шаге есть просто
g*n(Gn-1) = Gn-1.
Условное максимальное приращение скорости составит при этом
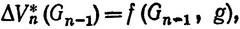
(3.56)
так как gn = Gn-1, а Gn = 0 по условию задачи.
Для выбора веса (n-1)-й ступени важен вес Gn-2, оставшийся после сбрасывания (n-2)-й ступени:
Gn-2 = Gn-1 + gn-1.
Условное оптимальное управление на предпоследнем (n-1)-м шаге, как мы уже знаем, следует выбрать таким образом, чтобы добиться максимума суммы двух приращений скорости на n-м и (n-1)-м шагах, т. е. иметь
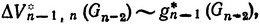
где
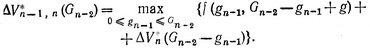
(3.57)
По аналогии условное оптимальное управление на любом j-м шаге определяется следующим образом:
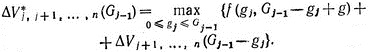
(3.58)
После оптимизации веса первой ступени g*1 при движении от начала к концу задачи находится оптимальное распределение веса ступеней (оптимальные управления), при котором контейнеру с полезной нагрузкой дается максимальное приращение скорости ΔV*.
Для того чтобы перейти к конкретному решению задачи, необходимо знать функцию (3.55). Получим выражение для этой функции исходя из законов механики при упрощающих предположениях о соотношении между расходом топлива и тягой двигателей.
Согласно второму закону Ньютона закон движения ракеты есть
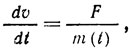
где F - сила тяги двигателей, m(t) - полная масса, которую имеет ракета в данный момент времени t. Предположим, что на каждой ступени ракеты установлены одинаковые двигатели и соотношение между силой тяги F и удельным расходом топлива p - линейное:
F = ap,
где a - постоянный коэффициент.
Будем считать также, что у каждой ступени вес двигателей и оборудования мал по сравнению с весом топлива. Тогда время расходования топлива Δt зависит от веса ступени;
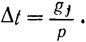
Как известно, масса любого тела пропорциональна его весу, поэтому имеем право написать
m{t) = q (Gj + gj + g - pt),
q - коэффициент пропорциональности.
Приращение скорости после срабатывания j-й ступени составляет
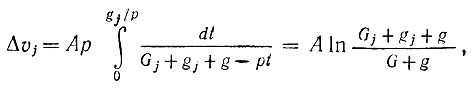
(3.59)
где 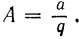
Это и есть искомая функция (3.55).
Пусть ракета должна иметь три ступени, т. е. задача должна решаться в три шага (n = 3). Приращение скорости на третьем шаге (3.56) составит
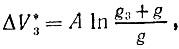
так как G3 = 0, поскольку после срабатывания третьей ступени она сбрасывается. Условное оптимальное управление есть g3(G2) = g3.
Согласно выражению (3.57) условное максимальное приращение скорости после срабатывания двух последних ступеней при любом весе первой ступени составит:
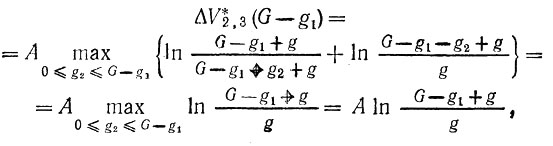
так как окончательное выражение не зависит от g2 (максимальное приращение скорости не зависит от веса g2).
Уловное максимальное приращение после срабатывания трех ступеней есть
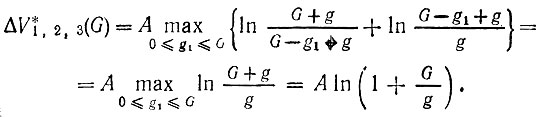
(3.60)
Этот результат означает, что можно произвольным образом распределять вес G между ступенями ракеты, и при этом максимальное приращение скорости логарифмически зависит лишь от отношения собственного веса ракеты к весу контейнера с полезной нагрузкой. Формула (3.60), которую мы получили методом динамического программирования, в несколько ином виде хорошо известна в теории реактивного движения и носит название формулы Циолковского.
Независимость максимального приращения скорости от распределения веса между ступенями явилась следствием упрощающих предположений, использованных в условии задачи. Нетрудно показать, например, что учет определенного соотношения между весом топлива и остального оборудования каждой ступени и других факторов приводит к настоящей задаче отыскания максимума логарифмической функции. Однако для полного решения задачи в общем случае, по-видимому, придется воспользоваться численным счетом.
Рассмотренная задача относится к задачам с резервированием средств. Действительно, мы рассматривали процесс из т шагов и перед каждым из них должны были решать, какую часть неистраченного веса ракеты истратить на данную ступень, а какую резервировать для следующих. Похожая задача распределения с резервированием возникает, если у нас имеется всего одна отрасль производства и некоторое количество средств Q0, которое можно вкладывать в производство не полностью, а частично вкладывать и частично резервировать. Средства xj, вложенные в производство на j-м этапе, приносят доход fj (xj) и частично расходуются. Требуется так распределить все средства по этапам, чтобы получить максимальный доход.
Эта задача легко сводится к рассмотренной выше (см. § 2) задаче распределения ресурсов между двумя отраслями, если считать, что резервированные средства вкладываются в некоторую фиктивную вторую отрасль производства, в которой, однако, средства не расходуются, но и не дают дохода. В этом случае решение задачи проводится точно так же, как решение задачи распределения ресурсов.
Покажем, как, пользуясь понятием фазового пространства, наглядно изобразить процесс решения задач распределения (см. § 3).
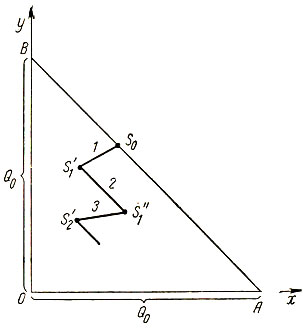
Рис. 3.1
Если система S, которую мы оптимизируем, представляет собой две отрасли производства, между которыми производится распределение ресурсов Q0, то движение этой системы можно изобразить точкой в двумерном фазовом пространстве (рис. 3.1), где по осям координат отложены количества средств x≥0 и y≥0, вкладываемые в каждую отрасль:
x + y ≤ Q0.(3.61)
Фазовым пространством, в котором может находиться система S, является треугольник АОВ. Областью начальных состояний системы является любая точка прямой АВ, так как по условию задачи сумма начальных вложений в обе отрасли равна начальному количеству ресурсов x1 + y1 ≤ Q0.
Что касается области конечных состояний системы  , то в зависимости от постановки задачи этой областью может Выть либо весь треугольник АОВ, если в качестве ограничения задачи используется лишь условие (3.61), либо только точка О, если дополнительно ставится условие, что выделенные средства должны быть истрачены полностью.
, то в зависимости от постановки задачи этой областью может Выть либо весь треугольник АОВ, если в качестве ограничения задачи используется лишь условие (3.61), либо только точка О, если дополнительно ставится условие, что выделенные средства должны быть истрачены полностью.
Если рассматриваемая задача является дискретной, то траектория движения системы S в фазовом пространстве изображается ломаной линией (рис. 3.1), состоящей из отрезков прямых, обозначающих расходование и перераспределение средств.
Допустим, выбрано некоторое начальное распределение средств, и состояние системы описывается точкой S0, находящейся на прямой АВ.
Рассмотрим первый шаг. Расходование только средств x приводит к тому, что точка S движется параллельно оси x по направлению к оси y; при этом y = const. При расходовании только средств у точки S движется параллельно оси y и x = const. Одновременное расходование средств x и y вызывает движение точка S внутрь треугольника АОВ под различными углами к осям хну таким образом, что проекции положения этой точки движутся по осям x и y по направлению к началу координат.
После завершения первого шага (отрезок 1, рис. 3.1) Иароизводится перераспределение оставшихся ресурсов (отрезок 2), при котором сумма ресурсов сохраняется. Поэтому точка S перемещается вдоль прямой, параллельной АВ, из положения S'1 в S"1. Из последней точки производится второй шаг (отрезок 3), потом опять перераспределение оставшихся ресурсов и т. д. до тех пор, пока либо не будет выполнено заданное число шагов, либо мы не придем в конечную точку Sn = 0.
В частном случае задачи распределения с резервированием и полным расходованием отпущенных ресурсов на каждом шаге траектория движения системы в фазовом пространстве строится еще проще. По оси x откладывается количество расходуемых ресурсов, по оси y - резервируемое количество ресурсов. На первом шаге требование полного расходования ресурсов x приводит к тому, что движение системы производится до пересечения траектории с осью y. Далее производится перераспределение путем выдачи ресурсов из резерва (движение параллельно прямой АВ) и опять полное расходование. В конце концов после расходования всех имеющихся ресурсов система после n шагов придет в точку Sn = 0.
До сих пор во всех рассматривавшихся задачах распределения ресурсов между отраслями производства получавшийся доход (выигрыш) никак не использовался в производстве. Интересно, однако, рассмотреть случай, когда доход, полученный в производстве частично или полностью вкладывается обратно в производство вместе с начальными ресурсами. В зависимости от постановки задачи можно искать оптимальное управление, которое, например, обращает в максимум общую сумму средств (доход плюс сохранившиеся основные средства) либо обращает в максимум только чистый доход.
В качестве примера задачи о распределении ресурсов с вложением доходов в производство рассмотрим случай, когда доход полностью вкладывается в две отрасли производства и требуется максимизировать сумму всех имеющихся средств (доход плюс основные средства обеих отраслей) после n-го шага.
Значение критерия в этой задаче полностью определяется величиной средств, имеющихся после завершения n-го шага, т. е. W = wn, а его приращения на предшествующих этапах следует принять равными 0. Критерий такого вида является частным случаем аддитивного критерия.
Обозначим количество средств в начале j-го (конце (j-1)-го) шага через Zj-1(Z0 - начальное количество средств) и введем функции изменения средств в первой и второй отраслях производства Fj (xj) и Φj(Zj-1 - xj), где xj - количество средств, вкладываемых в первую отрасль, (Zj-1 - xj) - вкладываемых во вторую отрасль в начале j-го шага.
Условный максимальный доход на последнем n-м шаге при любом исходе Zn-1 предпоследнего шага есть
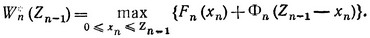
Этот доход получается при условном оптимальном управлении
xn*(Zn-1).
Исход (n-1)-го шага определяется исходом (n-2)-го шага Zn-2 и управлением xn-1:
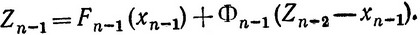
Поэтому для любого исхода (n-2)-го шага выбирается условное оптимальное управление из условия, чтобы получить
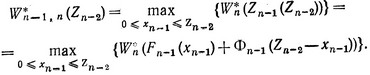
Для произвольного j-го шага условное оптимальное (управление x*j(Zj-1) обеспечивает получение
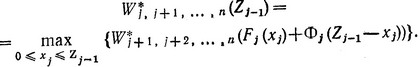
Когда мы дойдем до первого шага, то получим соответственно оптимальное управление x*1 и максимальное значение искомого критерия
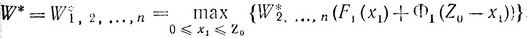
После того как мы нашли W* и x*1, двигаясь от начала к концу, находим оптимальные управления и количества средств, имеющих после завершения каждого шага:
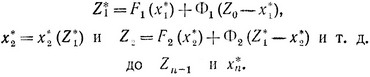
Рассмотрим конкретный пример. Пусть на предприятии запущены, но продолжают совершенствоваться два технологических процесса производства одного и того же продукта. Согласно проекту стоимость продукта, выпущенного первым процессом, должна в течение первого года вдвое, а в каждый из двух последующих лет втрое превышать стоимость исходного сырья. Соответственно стоимость продукта, выпущенного вторым процессом, должна в течение первого года равняться стоимости исходного сырья, в течение второго года превышать вдвое эту стоимость и в течение третьего года - вчетверо. В начале первого года на покупку сырья выделены средства z0 = 1 (тыс. руб.), причем решено, что в течение трех лет, пока эти процессы отлаживаются, все средства, получаемые от реализации произведенного продукта, используются только для покупки нового сырья. Требуется в этих условиях так спланировать распределение сырья между этими технологическими процессами, чтобы к концу третьего года максимизировать сумму всех средств (доходов), получаемых от реализации произведенного продукта.
Согласно условию функции изменения средств имеют вид (Fj - функция первого процесса, Φj - функция второго процесса):
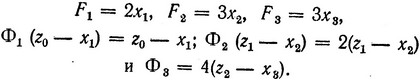
Условный максимальный доход в конце третьего года составит
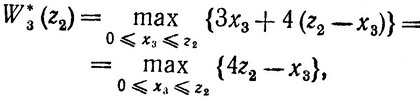
где
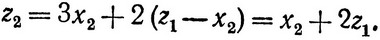
Условный максимальный доход за два последних года составит
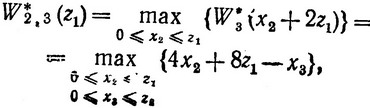
где в свою очередь z1 = 2x1 + (z0 - x1) = x1 + z0 определяется управлением x1.
Полный доход за все три года составит
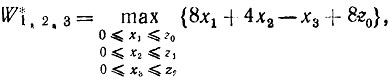
(*)
где максимум берется по всем возможным комбинациям x1, x2, x3. Так как z0 = 1, то x1 = 0,1. При x1 = 0 получаем z1 = 1, x2 = 0,1 и при x1 = 1 получаем z1 = 2, x2 = 0, 1, 2. Далее, поскольку z2 = x2 + 2z1, находим, что z1 = 1 приводит к z2 = 2 и z2 = 3, а z1 = 2 приводит к z2 = 4, 5, 6. Затем берутся всевозможные значения 0≤x3≤z2 при значениях z2 = 2, 3, 4, 5, 6. Последовательность возможных комбинаций значений xj и zj бывает удобно представить как ветвящуюся цепь следующего вида:
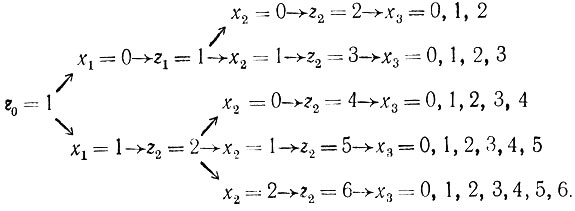
Возможные комбинации x1, x2, x3 определяются путем прослеживания ветвей. Эти комбинации подставляются в выражение (*), и наибольшее из полученных чисел как раз и есть максимально возможный доход, который в нашем случае равен 24 (тыс. руб.). Этот доход получается при использовании управления x1* = 1, x2* = 2, x3* = 0, что означает: в течение первых двух лет отдавать все закупаемое сырье первому процессу, а на третий год отдавать все сырье второму процессу.
Итак, мы видим, что решение этой задачи оказалось не сложнее решенных ранее задач распределения ресурсов. Более того, можно показать, что если функции Fj (xj) и Φj(Zj-1 - xj) являются неубывающими функциями своих аргументов: го оптимальное управление состоит в том, чтобы вбиваться максимальной выгоды на каждом шаге в отдельности. Это означает, что можно оптимизировать каждый шаг в отдельности, не заботясь об остальных, и при этом все равно получится максимальная выгода в конце процесса. Задачи, которые допускают решение таким образом, называются вырожденными.
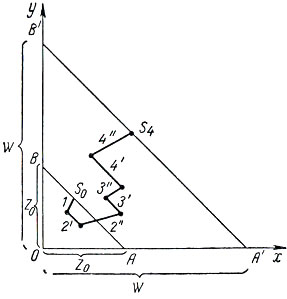
Рис. 3.2
Поведение системы S, соответствующей только что рассмотренной задаче, можно также представить в двумерном фазовом пространстве (рис. 3.2), где по осям x и y отложены количества ресурсов (средств), вложенных в первую и вторую отрасли производства. Однако фазовым пространством для данной задачи является весь первый квадрант, так как теперь ресурсы могут не только уменьшаться, но и расти. Траектория опять состоит из отрезков прямых, отражающих затраты (отрезок 1), накопление (отрезки 2", 3", 4") и перераспределение (отрезки 2', 3' 4') ресурсов. Решение задачи сводится к определению такой траектории в фазовом пространстве, чтобы вывести систему после n-го шага на прямую А'В', параллельную АВ и отстоящую как можно дальше от начала координат. Отметим, что для данной задачи значение критерия W непосредственно определяется расстоянием точек А' и В' от начала координат. Конечно, масштаб по осям x и y должен быть при этом задан в соответствующих единицах.
Итак, мы убедились в том, что задача о распределении ресурсов с обратным полным вложением дохода в производство решается довольно просто. В случае, когда доход, получаемый на каждом шаге, вкладывается в производство не полностью, а лишь частично, решение несколько усложняется. Однако мы не будем на нем останавливаться, а перейдем к рассмотрению более сложной задачи распределения ресурсов с последействием.
До сих пор мы рассматривали распределение ресурсов между двумя совершенно равноправными отраслями производства, одинаково приносившими доход (если не считать задачи о распределении с резервированием ресурсов, где искусственно вводилась фиктивная отрасль с нулевым доходом). Однако может иметь место и такая ситуация, когда дна из отраслей не способна сама получать доход и выступает в качестве вспомогательной, "поддерживающей" по отношению к основной отрасли; однако в результате деятельности этой вспомогательной отрасли доход основной отрасли определенным образом увеличивается. В практике хозяйственной деятельности часто складывается ситуация, тогда деятельность вспомогательной отрасли сказывается ишь спустя какое-то количество времени, т. е, лишь через несколько шагов с момента вложения средств в эту вспомогательную отрасль. Такое влияние деятельности вспомогательной отрасли на доход основной отрасли на данном эта-ре и называется последействием.
Одним из наиболее ярких примеров задачи распределения ресурсов с последействием является задача планирования производства с ориентированием на достижения научно-технического прогресса. Эта задача кратко формулируется следующим образом [11, 15].
При исходном запасе ресурсов Z0 и возможности полностью использовать все имеющиеся в начале каждого года ресурсы, вкладывая их как в производство, так и на содержание научной лаборатории, требуется найти такое управление на период n лет, при котором общее количество имеющихся ресурсов Zn, т. е. чистый доход плюс оставшаяся класть основных средств, в конце периода окажется максимальным.
Несколько конкретизируем условия задачи. Как обычно считается, что количество ресурсов x, будучи вложено в производство, по истечении некоторого периода времени, например j-го года, превращается в другое количество ресурсов Fj (x), причем возможно любое из соотношений:
Fj (x)<x; Fj (x) = x; Fj (x)>x.
Известно, что научная лаборатория, проводя исследования производственного процесса, находит пути его улучшения, в результате чего после внедрения этих улучшений в производство повышается доходность последнего, т. е. Ко прошествии k лет оказывается Fk (x) > F1 (x). Для простоты функцию Fk (x) будем считать неубывающей.
Однако такое повышение доходности не дается даром. На содержание лаборатории нужно затратить в k-м году ее существования определенные средства, которые мы обозначим как Λ(k-1). Считается, что эти средства, как таковые, теряются безвозвратно. Поскольку ничего не сказано о деятельности ("научном заделе") лаборатории до начала рассматриваемого периода, можно считать, что лаборатория создается в первый год этого периода и при этом Λ(0) - первоначальные затраты на создание и содержание лаборатории в течение первого года. Предположим, что если в течение какого-то времени средства на лабораторию не отпускаются, то и достигнутый уровень доходности производства в течение этого времени также сохраняется прежним, причем перерыв в финансировании лаборатории не сказывается на эффективности ее функционирования.
Перейдем к решению задачи. Схема решения оказывается во многом похожей на решение задачи распределения с вложением доходов обратно в производство. Однако теперь при распределении средств перед началом каждого шага (года) решается следующий вопрос: отпускать заданное количество денег для лаборатории или не отпускать, т. е. имеется выбор между двумя управлениями U- (не отпускать средств), U+ (отпускать средства).
Состояние системы (производство плюс лаборатория) описывается двумя параметрами: полным количеством имеющихся средств и числом лет k, в течение которых функционировала лаборатория к данному моменту.
Допустим, к концу (n-1)-го шага получено количество средств Zn-1 и лаборатория работала kn-1 (0≤kn-1≤n-1) лет. Если после этого на n-м шаге применить управление U-, то мы получим доход
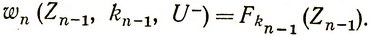
(3.62)
Если применить управление U+, то получим
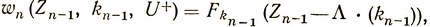
(3.63)
так как в этом случае в производство вкладываются только те средства, которые остаются после финансирования лаборатории. Поскольку мы условились о том, что функция Fkn-1 - неубывающая, то величина (3.62) всегда больше величины (3.63), и поэтому оптимальное управление на последнем шаге независимо от исхода предпоследнего шага есть U- - не отпускать средств на лабораторию. Соответствующий безусловный максимальный выигрыш есть
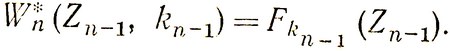
(3.64)
Исход (n-1)-го шага определяется исходом (n-2)-го шага. Если используется управление U-, то имеем
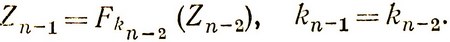
При управлении U+ имеем
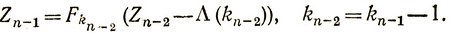
Выигрыш за последние два шага при управлении U- последнем и предпоследнем шагах составляет
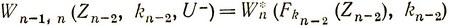
(3.65)
или с учетом (3.64)
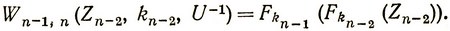
Соответственно выигрыш при управлении U+, также учитывая (3.64), запишем в виде
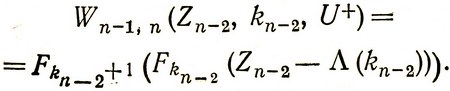
(3.66)
Выбор оптимального управления U- или U+ производится при сравнении выигрышей (3.65) и (3.66); условным максимальным выигрышем будет величина
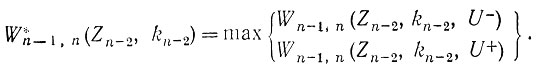
Поступая аналогично для любого j-го шага, условный максимальный выигрыш и условное оптимальное управление U- или U+ получаются при выборе максимальной величины согласно выражению вида
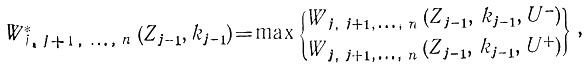
(3.68)
где
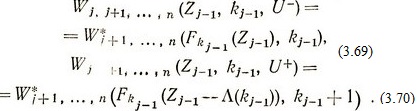
Для первого шага Zj-1 = Z0 и kj-1 = k0 = 0 из (3.68), (3.69), (3.70) получаем выражение полного максимального выигрыша:
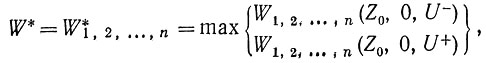
(3.71)
где
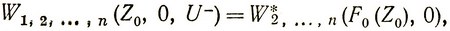
(3.72)
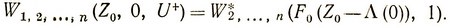
(3.73)
Оптимальное управление на первом шаге будет U-, если величина (3.72) больше величины (3.73), и U+, если наоборот.
После этого движение начинается в обратном направлении: находится результат первого шага при оптимальном управлении (Z1*, k1*), по нему определяется оптимальное управление на втором шаге, затем результат второго шага (Z2*, k2*) и так далее до последнего шага. На этом решение задачи заканчивается.
Этим мы закончим рассмотрение задач распределения ресурсов и перейдем к еще одному виду задач, которые решаются методом динамического программирования - задачам о замене оборудования.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'