
§ 5. Вычислительный метод динамического программирования для задачи распределения с двумя ограничениями и задачи с двумя переменными
Задача распределения с двумя ограничениями формулируется следующим образом: определить
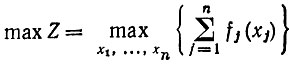
при ограничениях
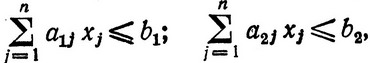
(3.24)
xj>0; j = 1, 2, ..., n; xj - все целочисленные.
Из тех же соображений, что и в задаче с одним ограничением, будем предполагать, что все a1j, a2j и b1, b2 целые и положительные числа.
Задача с двумя ограничениями, естественно, возникает тогда, когда в процессе распределения участвуют два источника ограниченных ресурсов. На j-м шаге выбирается величина xj, одновременно определяющая соответственно количества a1jxj и a2jxj ресурсов первого и второго типов, Предназначенных для использования на этом шаге.
Поскольку задача (3.24) решается аналогично задаче (3.1) с той лишь разницей, что теперь используются два параметра состояния, то не будем приводить всех рассуждений, необходимых для вывода реккурентных соотношений, а запишем сразу окончательные результаты. Имеем функцию состояния на первом шаге:
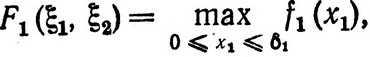
(3.25)
где 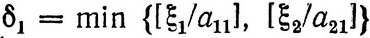 выбирается таким образом, чтобы не нарушались ограничения. Реккурентное соотношение для вычисления других функций состояния имеет вид:
выбирается таким образом, чтобы не нарушались ограничения. Реккурентное соотношение для вычисления других функций состояния имеет вид:
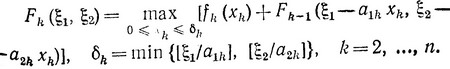
(3.26)
Искомая величина Z* = max Z есть
Z* = Fn (b1, b2).
Одновременно с Fn (b1, b2) на последнем n-м шаге находится оптимальное управление на этом шаге x*n. Оптимальные значения остальных управлений выбираются среди уже вычисленных совместно с величинами Fn (b1, b2) условных оптимальных управлений 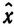 k (ξ1, ξ2). Этот выбор производится с помощью соотношений вида
k (ξ1, ξ2). Этот выбор производится с помощью соотношений вида
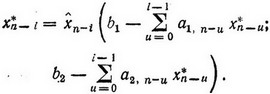
(3.27)
Если в задаче распределения два ограниченных источника ресурсов на каждом шаге могут распределяться независимо, а выгода от каждого шага является в общем случае функцией использованного количества обоих ресурсов, то задача приобретает следующий вид:
найти
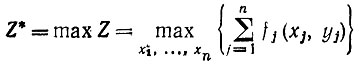
(3.28)
при ограничениях
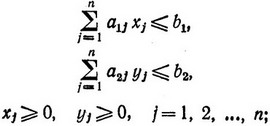
все xj и yj - целочисленные. Все a1ja2j и b1, b2 также считаются целочисленными и положительными.
Решение этой задачи опять проводится аналогично решению задач (3.1) и (3.24), но теперь на j-м шаге необходимо выбирать значения двух переменных xj и yj. Как и в задаче (3.24), на каждом шаге используются два параметра состояния, определяющих количества используемых ресурсов каждого вида.
Функция состояния на первом шаге записывается в виде
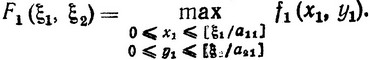
(3.29)
Реккурентные соотношения для вычисления функций состояния на любом шаге k = 2, ..., n имеют вид:
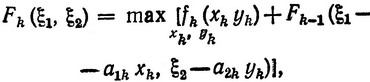
(3.30)
где xk также может принимать значения 0, 1, ..., [ξ1/a1k] и yk - значения 0, 1, ..., [ξ2/a2k]. В общем случае максимум по xk и yk находится прямым перебором возможных комбинаций этих переменных и вычисления для каждой из комбинаций величин
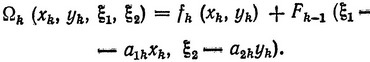
Таким образом, решение задач распределения с двумя ограничениями и двумя переменными (управлениями) в общем случае требует значительного увеличения объема вычислений. Поэтому задачи с двумя переменными обычно удается решать только с помощью больших электронных цифровых вычислительных машин (ЭВМ). Задачи с тремя переменными или (и) тремя параметрами состояния в ряде случаев также могут быть решены на больших ЭВМ. Во всяком случае задачи с четырьмя переменными,по-видимому, представляют тот предел, который в настоящее время в некоторых случаях еще может быть преодолен с помощью самых больших и быстродействующих ЭВМ.
Для того чтобы продемонстрировать эту слабую сторону вычислительного метода динамического программирования, сравним эффективность последнего с описанным в гл. I, §5 симплексным методом на примере решения задачи линейного программирования
найти:
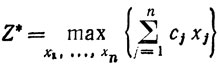
при ограничениях
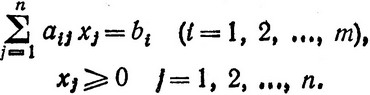
(3.31)
Предположим сначала, что все aij≥0.
Эта задача может рассматриваться как n-шаговый процесс, в котором на каждом j-м шаге выбирается значение величины xj, т. е. задача в такой постановке может решаться методами динамического программирования с одним переменным и m параметрами состояния.
Функция состояния соответственно будет иметь вид:
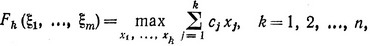
где максимум берется по всем x1, ..., xk, удовлетворяющим условиям
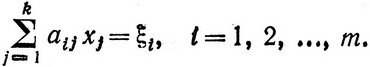
Реккурентные соотношения для вычисления функций состояния записываются в виде
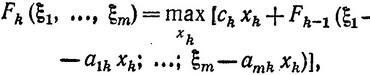
(3.32)
где xk меняется в интервале от 0 до min {[ξi/aik]}, k = 2, ..., n.
Если число параметров состояния ξ1 велико, то объем вычислений методом динамического программирования становится чрезмерно большим. Например, при наличии 100 ограничений (m = 100) и соответственно 100 параметров состояния и при условии, если каждый из них принимает 100 значений, общее количество значений функции Fk (ξ1, ..., ξm) достигает 10200. Это столь большое количество, что для его вычисления на ЭВМ со скоростью 106 значений Fk (ξ1, ..., ξm) в секунду потребуется более 10186 лет. Ясно, что задачу (3.31) с таким числом параметров состояния невозможно решить методом динамического программирования, тогда как решение этой задачи на ЭВМ симплексным методом часто не представляет большого труда. Симплексный метод зачастую оказывается эффективнее даже при наличии только одного или двух ограничений.
В том случае, если в задаче (3.31) некоторые aij<0, решение методом динамического программирования еще iee усложняется, так как наибольшее значение ξi, для которого должна быть вычислена функция Fk-1 в (3.32), может быть уже не равно bi. Во всяком случае оказывается трудно указать точно область определения каждого ξi.
Итак, мы рассмотрели вычислительный метод динамического программирования на примере задачи распределения. Однако, как уже указывалось выше, метод динамикою программирования может с успехом использоваться решении самых различных задач многошагового принятия решений. Забегая вперед, укажем, что вид реккурентных соотношений, используемых для вычисления функций состояния Fk(ξ), в различных задачах оказывается существо различным, т. е. вид этих соотношений зависит от структуры решаемой задачи. Для того чтобы облегчить в дальнейшем понимание проса решения различных конкретных задач, в следующем параграфе будет дана более общая постановка задачи динамического программирования.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'