
§ 6. Задачи с линейными ограничениями и выпуклыми (вогнутыми) функциями цели
Рассмотрим теперь решение еще одного вида упрощенных задач, у которых нелинейной (выпуклой или вогнутой) является только функция цели.
Будем, например, искать решение задачи с линейными ограничениями вида
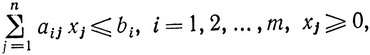
(2.28)
обращающее в максимум вогнутую функцию цели f (X) = f(x1, ..., xn).
Предположим, что функция f (X) имеет непрерывные первые частные производные в каждой точке множества допустимых решений. Выберем некоторое допустимое решение X0 и определим градиент 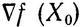 функции f (X). Напомним, что если
функции f (X). Напомним, что если 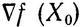 = 0, то уже точка X0 может являться решением задачи. Предположим, однако, что градиент
= 0, то уже точка X0 может являться решением задачи. Предположим, однако, что градиент 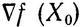 отличен от нуля, т. е. выбранная точка X0 заведомо не является решением задачи. Необходимо найти Такую последовательность точек X1, X2, ..., чтобы каждая следующая точка была ближе к оптимальному решению, т. е. последовательность точек, для которых f (X1)>f(X0), f(X2)>f(X1) и т. д.
отличен от нуля, т. е. выбранная точка X0 заведомо не является решением задачи. Необходимо найти Такую последовательность точек X1, X2, ..., чтобы каждая следующая точка была ближе к оптимальному решению, т. е. последовательность точек, для которых f (X1)>f(X0), f(X2)>f(X1) и т. д.
Будем искать точку X1, обеспечивающую лучшее приближение к оптимальному решению, чем точка X0, следующим образом. Положим X1 = X0 + αd0, где α - некоторое число, d0 = 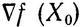 - градиент функции f в точке X0, т. е. потребуем, чтобы перемещение из точки X0 в точку x1 происходило по направлению градиента на расстояние, пропорциональное величине градиента. Если ищется максимум f (X), то следует брать α>0.
- градиент функции f в точке X0, т. е. потребуем, чтобы перемещение из точки X0 в точку x1 происходило по направлению градиента на расстояние, пропорциональное величине градиента. Если ищется максимум f (X), то следует брать α>0.
При переходе от X0 к X1, очевидно, имеются две возможности:
Случай 1. Существует такое ε, что X1 = X0 + αd0 является допустимым решением при всех α, определяемых неравенством 0≤α≤ε.
Случай 2. Не существует α>0 такого, чтобы X1 = X0 + αd0 было допустимым решением.
Рассмотрим сначала первый случай и покажем, что существует α>0, при котором X1 = X0 + αd0 является допустимым решением и f (X1)>f(X0). По условию X1 = X0 + αd0 - допустимое решение для всех 0≤α≤ε; однако это еще не значит, что для всех этих αf (X1)>f(X0). Согласно теореме Лагранжа можно написать [см. 16]:
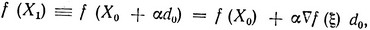
где ξ = X1 = X0 + αθd0, 0≤θ≤1.
Неравенство f (X1)>f(X0) выполняется, если ∇f (ξ) d0>0, что справедливо в задаче на максимум по крайней мере для X1 и некоторого δ>0, таких, что |X1-X0|<δ. Следовательно, если α удовлетворяет соотношению 0<α< min (ε, δ), то X1 ≡ X0 + αd0 является допустимым решением и f (X1)>f(X0).
Ясно, что желательно получить возможно большее значение f (X1), но так, чтобы X1 оставалось допустимым решением. Поэтому найдем наибольшее αmax ≡ ε0, для которого X1 ≡ X0 + ε0d0 является еще допустимым решением. Для этого подставим X1 в ограничения задачи и условие xj≥0:
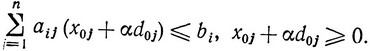
(2.29)
Величина а должна выбираться такой, чтобы, во-первых, не нарушались ограничения и, во-вторых, все компоненты xj оставались неотрицательными.
Поэтому из (2.29) получаем два условия, которым должна удовлетворять максимальная величина α:
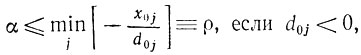
(2.30)
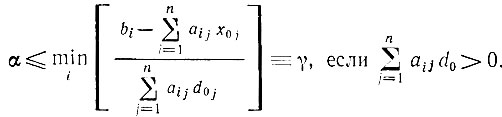
Очевидно, следует принять ε0 = min (ρ, γ). Однако неправильно было бы сразу положить α = ε0, поскольку ∇f (X) меняется при разных X1 и может случиться, что при большом а, когда |X1 - X0|>δ, будет f (X0 + αd0)<f (X0). Поэтому следует взять такое α, 0<α<ε00, которое максимизирует f (X0 + αd0).
Самый простой метод определения необходимого α состоит в делении интервала 0<α≤ε0 на равные части по Δα точками αk = kΔα и вычислении f (X0 + αkd0) для каждого k. Из всех f (X0 + αkd0) следует выбрать наибольшее, и αk, дающее этот максимум, как раз и является искомым. В частности, для задачи линейного программирования, когда 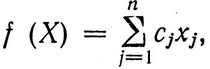 величина ∇f (X) не зависит от X, и можно положить α = ε0, так как f (X0 + αd0) линейно возрастает по α. Таким образом, когда функция цели линейна, следует двигаться до границы области допустимых решений, и максимум достигается в экстремальной точке.
величина ∇f (X) не зависит от X, и можно положить α = ε0, так как f (X0 + αd0) линейно возрастает по α. Таким образом, когда функция цели линейна, следует двигаться до границы области допустимых решений, и максимум достигается в экстремальной точке.
Вернемся теперь ко второму случаю, когда сразу не существует α>0, при котором X1 = X0 + αd0 является допустимым решением, т. е. решение X0 находится на границе множества допустимых решений. При этом некоторые из ограничений или условий неотрицательности xj будут сразу нарушаться, если пытаться двигаться по направлению градиента. Определим, в каком направлении нужно двигаться, чтобы ограничения не нарушались, а значения функции цели f увеличивались. Отметим, что к случаю 2 можно прийти также после одного или нескольких изменений значений xj, согласно процедуре случая 1.
Поскольку в случае 2 мы лишены возможности двигаться вдоль направления ∇f (X), выберем другое направление, задаваемое некоторым вектором r, |r| = 1, r ≡ (r1, ..., rn). Скорость изменения функции f (X) при движении из точки X0 в направлении r определяется выражением
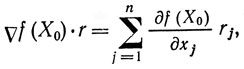
т. е. скалярным произведением векторов 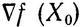 и r; величина
и r; величина 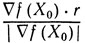 есть косинус угла между
есть косинус угла между 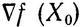 и r.
и r.
Запишем изменение переменной X в виде X1 = X0 + αr, считая, что α>0. Поскольку X1 должно быть допустимым решением, можно написать:
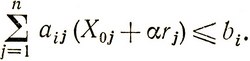
(2.31)
Так как точка X0, по определению, находится на границе множества допустимых решений, т. е. 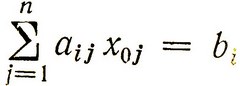 (для некоторого i), переход в точку X1 осуществляется таким образом, чтобы X1 также находилась на границе этого множества, поэтому
(для некоторого i), переход в точку X1 осуществляется таким образом, чтобы X1 также находилась на границе этого множества, поэтому
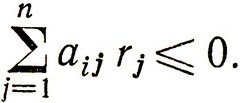
(2.32)
Теперь для того чтобы определить направление возрастания f (X) без нарушения ограничений, необходимо решить следующую задачу:
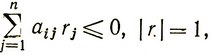
(2.33)
найти максимум z = 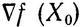 *r, т. е. найти такой вектор r, который образует наименьший угол с
*r, т. е. найти такой вектор r, который образует наименьший угол с 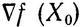 .
.
Можно использовать и более простые способы нахождения возможного r, например, потребовать выполнения условия
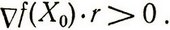
(2.34)
Предположим, что найден некоторый вектор r0, удовлетворяющий задаче (2.33) или условию (2.34) с ограничениями (2.32) Далее необходимо определить ρ и γ в соответствии с (2.30) и найти ε0, чтобы x1 = x0 + αr0 было допустимым решением задачи (2.28). Процесс движения из точки x1 в точку x2 продолжается, если из точки x1, можно найти направление, для которого ∇f(X1)r1>0. Когда некоторой точке окажется, что ∇f(Xk)rk≤0 для любого rk, которое не приводит к нарушению ограничений,процесс решения заканчивается.
Исписанную картину итерационного процесса можно проиллюстрировать геометрически на примере задачи с двумя переменными. Пусть надо найти максимум вогнутой функции f (X) на множестве М переменных (x1, x2). Линии уровня функции f (X) = const (c1<c2<c3) на плоскости переменных (x1, x2) изображены на рис. 2.5.
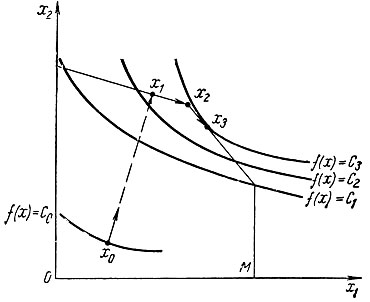
Рис. 2.5
Пусть за исходную точку взята точка X0. Градиент 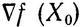 или d0 является вектором, нормальным к прямой, касательной линии уровня f (X) = C0 в точке X0, Из этой точки можно двигаться как можно дальше, пока не достигнем границы области допустимых решений. Как указывалось выше, это можно делать не всегда, однако в данном примере функция f (X) возрастает с увеличением а вплоть До границы области. Поэтому можно сразу двигаться в точку X1 = X0 + αd0, находящуюся на границе области допустимых решений.
или d0 является вектором, нормальным к прямой, касательной линии уровня f (X) = C0 в точке X0, Из этой точки можно двигаться как можно дальше, пока не достигнем границы области допустимых решений. Как указывалось выше, это можно делать не всегда, однако в данном примере функция f (X) возрастает с увеличением а вплоть До границы области. Поэтому можно сразу двигаться в точку X1 = X0 + αd0, находящуюся на границе области допустимых решений.
Из точки X1 уже нельзя двигаться в направлении градиента d1, так как при этом мы выйдем из области допустимых решений. Поэтому ищем вектор r1, решая задачу (2.33), вторая для точки X1 имеет только одно ограничение, задаваемое уравнением прямой, на которой находится эта точка.
На рис. 2.5 легко видеть, что вектор r1, составляющий меньший угол с d1, направлен вдоль соответствующего ограничения. Двигаясь в этом направлении, мы приходим в точку X2, где необходимо выбрать другой вектор r2. Далее, двигаясь вдоль вектора r2, приходим в точку X3 = X2 + αr2, в которой f (X) достигает максимума. Процедура определения величины α, для которого решение X3 является оптимальным, описана ранее.
Поясним сказанное выше численным примером. Возьмем уже рассматривавшуюся выше (см. § 6, гл. I и § 5, гл. II) задачу распределения ресурсов. Пренебрежем нелинейностью в ограничениях, сохранив нелинейность в функции цели. В результате имеем следующую задачу:
найти max f = 2 x1 - 0,1x12 + 3x2 - 0,1 x22
при ограничениях
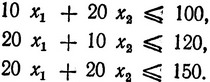
Выбираем в области допустимых решений начальную точку x01 = 1, x02 = 1, для которой f0 = 4,8. Вектор градиента в этой точке имеет компоненты
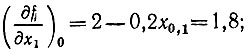
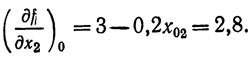
Движемся из точки (x01, x02) в направлении градиента:
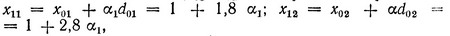
где α1 выбирается так, чтобы не нарушались ограничения:
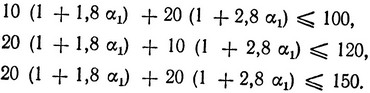
В соответствии с (2.30) 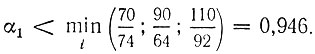 При таком движении мы прежде всего достигнем первого ограничения (проверка при значениях α<0,946 показывает, что двигаться можно вплоть до границы области допустимых решений). Итак, имеем x11 = 1 + 1,8*0,946 = 2,703, x12 = 1 + 2,8*0,946 = 3,649, f1 = 14,290. Далее следует двигаться вдоль первого ограничения. Задача определения направления движения (2.33) в данном случае имеет вид:
При таком движении мы прежде всего достигнем первого ограничения (проверка при значениях α<0,946 показывает, что двигаться можно вплоть до границы области допустимых решений). Итак, имеем x11 = 1 + 1,8*0,946 = 2,703, x12 = 1 + 2,8*0,946 = 3,649, f1 = 14,290. Далее следует двигаться вдоль первого ограничения. Задача определения направления движения (2.33) в данном случае имеет вид:
найти max z = (2 - 0,2 x11)r1 + (3 - 0,2x12)r2 = 1,459r1 + 2,270r2
при ограничениях
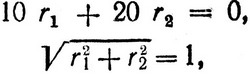
где r1 и r2 - компоненты вектора направления r. Решение этой задачи есть r1 = 0,894, r2 = -0,447. Таким образом, следует продолжать движение вдоль r, определяя α2 = 1,975 согласно (2.30), а также из второго и третьего ограничений, в которые подставляются значения x21 = 2,703 + 0,894α2 и x22 = 3,649 - 0,447α2. для различных значений α2 имеем:
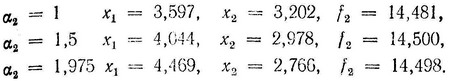
Таким образом, мы видим, что максимум f достигается где-то в окрестности α2 ≈ 1,5, причем само значение максимума очень слабо зависит от конкретных величин x1 и x2. Значение (α2)max, соответствующее этому максимуму, проще найти из условия ∇f*r = 0, или в нашем случае из выражения (2 - 0,2x1)*0,894 - (3 - 0,2x2)*0,447 = 0, где x1 = 2,703 + 0,894α2, x2 = 3,649 - 0,447α2.
Решая это уравнение относительно α2, имеем (α2) = 1,452, x1 = 4,001, x2 = 3,069, fmax = 14,666. На этом процесс решения заканчивается.
Итак, мы в общих чертах рассмотрели метод решения задачи максимизации вогнутой функции при линейных ограничениях. Решение подобной задачи минимизации выпуклой функции проводится аналогично, с той лишь разницей, что для минимизации функции цели приходится двигаться в сторону, противоположную градиенту, т. е. брать α<0.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'