
§ 7. Метод наискорейшего спуска (наискорейшего подъема)
Рассмотрим теперь решение задачи выпуклого программирования, заключающееся в минимизации выпуклой (максимизации вогнутой) функции
f (x) ≡ f (x1, ..., xn)(2.35)
на выпуклой области, определяемой неравенствами
gi (x1, ..., xn) ≤ 0, i = 1, 2, ..., m'.(2.36)
Метод наискорейшего подъема фактически уже использовался выше в § 6 при решении задач на максимум. Аналогичным по структуре является метод наискорейшего спуска, используемый при решении задач на минимум [3, 8, 9]. Общую схему решения этими методами задач выпуклого программирования можно представить следующим образом.
- Выбирается некоторая начальная точка, являющаяся допустимым решением задачи. В этой точке вычисляется градиент функции цели.
- Из начальной точки производится движение в направлении градиента до тех пор, пока функция цели возрастает (в задаче на максимум) или убывает (в задаче на минимум).
- По достижении точки, в которой функция цели получает наибольшее приращение, движение прекращается. В этой точке снова нужно найти значение градиента функции цели. Далее движение происходит в новом направлении градиента.
- Этот процесс продолжается до тех пор, пока не достигается граница области допустимых решений, и движение вдоль градиента становится невозможным.
- В достигнутой граничной точке определяется возможное направление, при движении вдоль которого функция цели возрастает. Оказывается, что наивыгоднейшим из возможных направлений является такое, для которого максимален косинус угла между этим направлением и градиентом функции цели. При решении задачи с линейными ограничениями наивыгоднейшее направление движения совпадало с соответствующим ограничением задачи.
- Процесс движения от точки к точке с возрастанием функции цели продолжается до тех пор, пока не достигается точка, в которой не существует ни одного возможного направления. Эта точка и является искомым оптимальным решением задачи.
Методы решения задач с линейными и нелинейными ограничениями отличаются в основном способами движения вдоль ограничений. Если при линейных ограничениях движение вдоль ограничений не приводит к выходу за границу области допустимых решений, то в случае нелинейных ограничений движение вдоль ограничений, определяющих выпуклую область, как правило, невозможно, поскольку мы быстро оказываемся вне области допустимых решений. Поэтому применяются различные способы движения, обеспечивающие выбор последовательности точек, расположенных вблизи границы и внутри области допустимых решений, или зигзагообразное движение вдоль границы с пересечением последней.
Перейдем к описанию решения общей задачи выпуклого программирования методом наискорейшего спуска. Прежде всего преобразуем саму задачу. Добавим к имеющимся n переменным дополнительную переменную xn+1 и дополнительное ограничение вида
f (x1, ..., xn) ≤ xn+1.
Тогда общая задача (2.35)-(2.36) может быть сформулирована следующим образом:
минимизировать линейную функцию
z = xn+1
при ограничениях
f (x1, ..., xn) - xn+1 ≤0,
gi (x1, ..., xn) ≤ 0 (i = 1, 2, ..., m').
Линейную функцию z можно представить в виде
z = p1x1 + p2x2 + ... + pnxn,(2.37)
где p1, ..., pn - заданные числа, выбранные таким образом, чтобы p1x1 + p2x2 + ... + pnxn = xn+1. Ограничения запишем в виде
ψi (x1, ..., xn) ≤ 0 (i = 1, 2, ..., m),(2.38)
где обозначено m = m'+1. Представленная в таком виде задача минимизации линейной функции (2.37) при нелинейных ограничениях вида (2.38), заданных гладкими выпуклыми функциями ψi (x1, ..., xn), называется канонической Формой общей задачи выпуклого программирования.
Во многих практических задачах сравнительно легко можно найти начальную точку X0, принадлежащую области допустимых решений. Однако, если возможное исходное решение неизвестно, оно может быть найдено, например, следующим образом.
Грубо оценим область определения переменных xj и возьмем из этой области любую точку X*. Подставим это решение в ограничения задачи. Если оказалось, что все
ψi (x1*, ..., xn*)≤0,
то выбранная точка может быть принята за начальную точку X0. Если ψi (x1*, ..., xn*)> 0, то введем дополнительную переменную ξ, такую, чтобы выполнялось неравенство
ψi (x1*, ..., xn*)≤ξ(2.39)
и будем искать минимум функции
u = ξ
способом, описанным выше, т. е. находя в точке X* градиент функции u, определяя длину допустимого продвижения и т. д. Для того чтобы найти начальную точку, в действительности необходимо лишь получить решение X0, для которого ξ≤0.
Пусть найдена начальная точка X0. В соответствии со сказанным выше и без ограничения общности изложения можно считать, что X0 лежит на границе области допустимых решений, поскольку в противном случае достаточно проделать один или несколько шагов из X0 в направлении градиента, чтобы достигнуть границы области.
Впрочем, продвижение непосредственно до границы области не является обязательным. Более того, на каждом шаге вычислений следует устанавливать значение некоторого достаточно малого параметра δk > 0 (k - номер шага), считая, что точка Xk-1 принадлежит границе области ψi (X) = 0, если выполняется неравенство
-δk<ψi(Xk-1)≤0.
Оно означает, что удаление точки Xk-1 от границы области допустимых решений неположительно и не больше чем - δk. Соответственно для начальной точки X0 можно написать
-δ1<ψi(X0)≤0.
Перейдем к определению направления ξ(1) = (ξ(1)1, ..., ξ(1)n) наикратчайшего спуска из точки X0. При движении в этом направлении функция цели z должна убывать, т. е. производная от z по направлению ξ должна быть
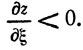
(2.40)
Напомним, что производной функции z по направлению ξ называется скорость изменения функции в этом направлении:
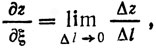
где Δz = z2 - z1 и Δl - приращение функции и приращение длины вдоль ξ соответственно.
Воспользовавшись известной формулой для производной сложной функции, можно написать:
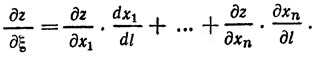
Правая часть этого выражения является скалярным произведением двух векторов: вектора градиента 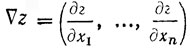 и вектора направления
и вектора направления
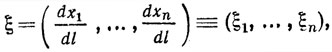
где
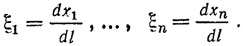
Градиент линейной функции z есть ∇z = (p1, ..., pn); поэтому можно в точке X0 записать условие (2.40) в виде
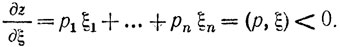
(2.41)
Кроме выполнения условия 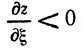 необходимо еще, чтобы направление ξ вело внутрь области допустимых решений, т. е. чтобы вдоль этого направления убывали все Функции ψi (x), или чтобы удовлетворялись неравенства
необходимо еще, чтобы направление ξ вело внутрь области допустимых решений, т. е. чтобы вдоль этого направления убывали все Функции ψi (x), или чтобы удовлетворялись неравенства
(∇ψi(X0),ξ)<0,(2.42)
где ∇ψi (X0) - градиент функции ψi в точке X0.
Величины (2.41) и (2.42) определяют соответственно скорость убывания функций z и ψi в направлении ξ. Для осуществления наискорейшего спуска при движении внутри области допустимых решений необходимо, чтобы величина (2.41), т. е. абсолютная скорость убывания функции z, была как можно большей при условии, что выполняется неравенство (2.42). Поэтому наряду с δ1>0 выберем произвольное достаточно малое λ1> 0, и направление ξ(1) определяем, решая следующую задачу линейного программирования:
минимизировать функцию
u = (p, ξ)(2.43)
при ограничениях
(∇ψi (X0), ξ) ≤-λ1.(2.44)
Для сходимости итерационного процесса необходимо, чтобы вектор направления ξ был ограниченным. Поэтому положим |ξ1| ≤c, ..., |ξn|≤c, где c - заданное число Многие известные методы решения задач выпуклого программирования отличаются способами нормализации, т. е. выбором величины c [9]. В частности, можно считать c = 1. таким образом, условие |ξi| ≤ c учитывается при решении задачи (2.43)-(2.44).
Пусть решением задачи (2.43)-(2.44) является величина η1, причем
min u = η1<-δ1 при ξ = ξ(1).
Тогда, меняя величину α в выражении
X = X0 + αξ(1),
двигаемся в направлении ξ(1) до тех пор, пока не встретим границу области допустимых решений. Величина α1 определяется как наименьший из положительных корней уравнений
ψi (X0 + αξ(1)) = 0 (i = 1, ..., m)
и называется шагом приближения. Далее находим точку X1 = X0 + α1ξ(1), в которой необходимо прекратить движение и искать новое направление движения, считая теперь точку X1 исходной. Полагаем δ2 = δ1, λ2 = λ1 и повторяем все вычисления, относившиеся к точке X0, пока на k-м шаге не придем к тому, что
min u = ηk≥-δk.
В случае 0>ηk≥-δk определяем αk, Xk и продолжаем процесс из точки Xk, считая теперь δk+1 = δk/2 и λk+1 = λk/2.
После некоторого числа шагов параметры δ и λ уменьшится настолько, что с достаточной степенью точности можно будет считать, что точка Xi принадлежит границе части допустимых решений, и min u = ηl+1 = 0. Это означает, что Xi является решением задачи, и итерационный процесс закончен.
Вообще говоря, из того факта, что на некотором шаге кажется ηl+1 = 0, т. е. из факта отсутствия направления спуска из точки Xl, еще нельзя сделать вывод, что точка Xl является решением задачи. Дело в том, что отсутствие направления спуска может быть следствием того, что недостаточно мало, и равенство нулю ηl+1 объясняется наличием поверхностей, на которых Xl в действительности не лежит, но уклонение от них меньше, чем δl+1. Известны способы проверки того, является ли Xl решением. Наиболее простой из них - в несколько раз уменьшить значение параметра δ и снова проделать вычисления ηl+1. Если окажется, что величина ηl+1 отличается от 0, то итерационный процесс следует продолжать до тех пор, пока не достигнем новой точки Xl, для которой ηl+1 = 0. После некоторого числа шагов решение задачи может быть найдено с заданной точностью.
Совершенно аналогично проводится решение задачи максимизации вогнутой функции методом наискорейшего подъема.
Обратимся к примеру. Опять возьмем уже рассмотренную выше (см. § 5 данной главы) задачу:
найти max f = 2x1 - 0,1x12 + 3x2 - 0,1x22
при ограничениях
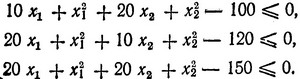
Ранее мы решали эту задачу о сепарабельными функциями приближенным методом, теперь же используем метод наискорейшего подъема.
Прежде всего представим задачу в канонической форме. Для этого в случае максимизации f надо ввести дополни, тельную переменную x3≤f и записать выражение (2.37) и новое ограничение в следующем виде:
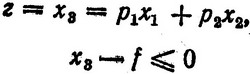
или
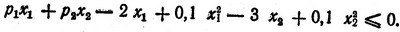
Выбор величин p1 и p2 до некоторой степени произволен, лишь бы всегда выполнялось ограничение, в которое они входят. Очевидно, p1 и p2 можно выбрать исходя из условий
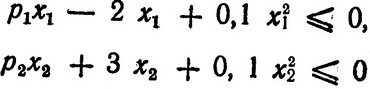
или
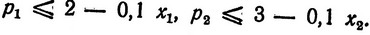
Ранее в § 5 мы уже оценивали, что (x1)max≤5, (x2)max≤5, следовательно, имеем p1≤1,5, p2≤2,5. Вместе с тем возрастание функции z происходит тем быстрее, чем больше p1 и p2; поэтому выбираем p1 = 1,5 и p2 = 2,5 и приходим к задаче:
найти max z = 1,5x1 + 2,5x2
при ограничениях
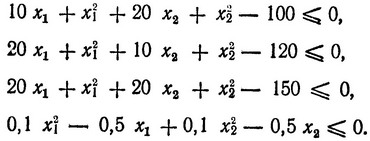
Выбираем начальную точку с координатами x01 = 1 и x02 = 1, которая заведомо принадлежит области допустимых решений, и из этой точки движемся в сторону возрастания z. Для этого находим ∇z:
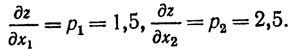
Так как ∇z не зависит от x1 и x2, то можно в принципе двигаться сразу до границы области допустимых решений, и при этом функция z (и вместе с ней и f, так как z ≤ f) рее время будет возрастать. Однако, если продвинуться до самой границы, дальнейшее движение вдоль ограничений будет практически невозможным, так как по крайней мере какое-нибудь одно ограничение будет нарушаться уже при самом малом шаге. Кроме того, также будут сильно сказываться ошибки вычислений, обычно накапливающиеся из-за округления результатов. Именно для этого вводится параметр δ1>0, ограничивающий приближение к границе. Выберем, например, δ1 = 1,01 и перепишем ограничения в виде
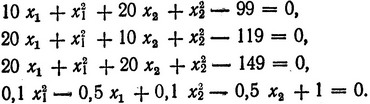
Подставим в эти уравнения значения x11 = 1 + 1,5α1, x12 = 1 + 2,5α1 и найдем (α1)max, при котором точка (x11, x12) еще находится в области, задаваемой ограничениями (аналогично тому, как это делалось в примере, рассмотренном в § 6). Получаем (α1)max = 0,838 и точку с координатами x11 = 2,257, x12 = 3,095, которую считаем находящейся на границе области допустимых решений. При этом z1 = 11,123.
Далее переходим к движению вдоль границы. Для этого ищем компоненты вектора ξ(1) (ξ1, ξ2), являющиеся решением следующей линейной задачи:
найти шах u = p1ξ1 + p2ξ2 = 1,5ξ1 + 2,5ξ2
при ограничениях
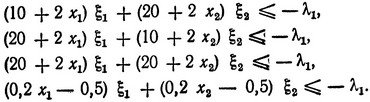
(*)
Здесь выражения в скобках есть компоненты вектора ∇ψi (например, 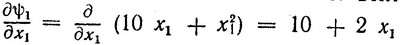 и т. д.), в которые следует подставить значения x1 = x11 = 2,257 и x2 = x12 = 3,095. Величину λ1>0 выберем несколько позже. В результате получаем систему ограничений в виде
и т. д.), в которые следует подставить значения x1 = x11 = 2,257 и x2 = x12 = 3,095. Величину λ1>0 выберем несколько позже. В результате получаем систему ограничений в виде
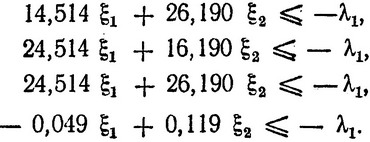
Эту задачу линейного программирования, конечно, можно решить симплексным методом, однако мы поступим проще. Для того чтобы функция z увеличилась, необходимо, чтобы было u>0, что, очевидно, будет иметь место, когда по крайней мере или ξ1>0, или ξ2>0. Значения ξ1 и ξ2, соответствующие крайним точкам многоугольника ограничений, можно легко найти, решая попарно уравнения, полученные из этой системы ограничений. Нетрудно убедиться, что только совместное решение последнего уравнения с остальными тремя дает ξ1> 0. При этом max u = 0,89λ1 достигается при значениях ξ1 = 8,65λ1, ξ2 = - 4,84λ1, получающихся при совместном решении уравнений
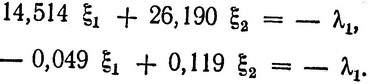
Согласно условиям |ξi|≤1 примем λ1 = 0,1; тогда ξ1 = 0,865, ξ2 = - 0,484 и max u = η1 ≈ 0,089.
Так как η1<δ1 (случай максимизации),то надо брать величину δ1/2 = δ2 и вычислять α2, используя ограничения в виде
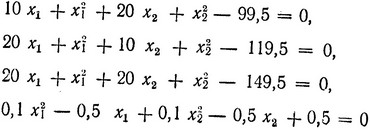
и переменные x1 = x21 = 2,257 + 0,865α2 и x2 = x22 = 3,095 - 0,484α2. Опять прежде всего будет нарушено первое ограничение, и оно определяет (α2)max = 0,668. Поэтому получаем после второго шага x21 = 2,835, x22 = 2,772. Для контроля правильности вычислений полезно бывает еще раз убедиться в том, что полученное решение удовлетворяет первым трем ограничениям. Что касается четвертого ограничения, то по условно оно удовлетворяется, если x1<5 и x2<5. Значение функции z также увеличилось в точке (x21, x22) и стало равным 11,183. После этого можно переходить к следующему шагу, определяя прежде всего ξ(2) (ξ1, ξ2) путем решения той же задачи линейного программирования (*), но при значениях x1 = 2,835 и x2 = 2,772. Как указано выше, процесс решения повторяется до тех пор, пока мы не получим max u = ηl+1 = 0. Количество шагов будет во многом определяться необходимой точностью решения задачи с учетом оговорок о проверке сходимости, сделанных выше. Естественно, что использование метода наискорейшего Куска (подъема) при расчетах вручную является весьма трудоемким, однако при наличии ЭВМ его применение не вызывает затруднений.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'