
§ 5. Приближенное решение задач с сепарабельными функциями
Изложим теперь общую идею приближенного решения задач с сепарабельными функциями. В математике известны методы, позволяющие заменить любую непрерывную функцию ломаной. Воспользуемся одним из этих методов и построим приближенную задачу к задаче (2.9)-(2.10), проводя кусочно-линейную аппроксимацию функций gij (xj) и fj (xj). Далее будет показано, как определяется оптимальное решение полученной приближенной задачи.
На примере функции одной переменной покажем, как проводится такая аппроксимация. Рассмотрим некоторую непрерывную функцию, определенную для всех x из интервала c1≤x≤c2 (рис. 2.4). Выберем на этом интервале r + 1 точку xk таким образом, чтобы x0 = c1, x1<x2<...<xk<... <xr = c2. Этим точкам будут соответствовать значения функции yk (xk). Соединим попарно точки xkyk и xk+1yk+1 при всех k = 0, ..., r - 1 отрезками прямых. В результате получится кусочно-линейная функция 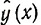 , которая аппроксимирует функцию y(x). Такая аппроксимация может быть сделана со сколь угодно большой точностью путем выбора соответствующего разбиения интервала c1≤x≤c2.
, которая аппроксимирует функцию y(x). Такая аппроксимация может быть сделана со сколь угодно большой точностью путем выбора соответствующего разбиения интервала c1≤x≤c2.
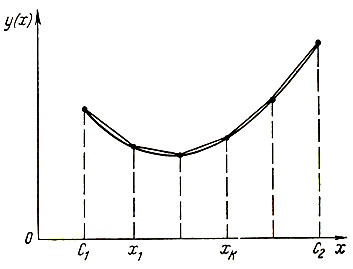
Рис. 2.4
Найдем аналитический вид функции 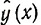 . Если x лежит в интервале xk≤x≤xk+1, то для
. Если x лежит в интервале xk≤x≤xk+1, то для 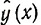 можно написать
можно написать
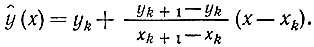
(2.18)
Любое значение x в интервале xk≤x≤xk+1 можно представить в виде x = λxk+1 + (1-λ)xk, где 0≤λ≤1.
Обозначим λ = λk+1, 1-λ = λk. Тогда имеем
x = λkxk + λk+1xk+1,(2.19)
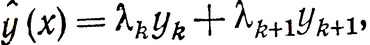
где λk + λk+1 = 1, λk ≥ 0, λk+1 ≥0.
Обобщая эти выражения таким образом, чтобы с их помощью определить любое x из c1≤x≤c2 и любую соответствующую функцию 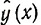 , можем написать:
, можем написать:
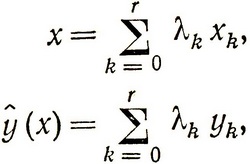
(2.20)
где 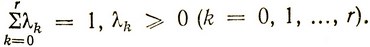
Если условиться, что отличными от нуля для каждых xk и yk являются лишь не более двух соседних λk, то функция (2.20) является аналитическим выражением кусочно-линейной функции, пример которой изображен на рис. 2.4.
Воспользуемся таким методом аппроксимации для построения функций, приближенных к gij(xj) и fj(xj). Будем считать, что в задаче (2.9)-(2.10) непрерывны все функции gij (xj) и fj (xj). Выберем на интервале c1j≤xj≤c2j, который может пробегать переменная xj (j = 1, 2, ..., n), rj + 1 точку xkj и, используя описанный выше метод аппроксимации, построим кусочно-линейные функции 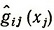 и
и 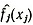 . Если интервал, который пробегает переменная xj, точно не известен, то предварительно необходимо грубо оценить, в каких пределах меняется xj, и производить разбиение этого расширенного интервала d1j<xj<d2j, где d1j<c1j и d2j>c2j. В результате мы получим задачу, приближенную к задаче (2.9)-(2.10):
. Если интервал, который пробегает переменная xj, точно не известен, то предварительно необходимо грубо оценить, в каких пределах меняется xj, и производить разбиение этого расширенного интервала d1j<xj<d2j, где d1j<c1j и d2j>c2j. В результате мы получим задачу, приближенную к задаче (2.9)-(2.10):
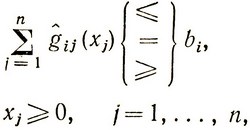
(2.21)
найти максимум (минимум) 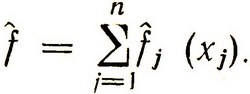
Все функции 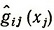 и
и 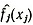 в соответствии с (2.20) можно записать в виде
в соответствии с (2.20) можно записать в виде
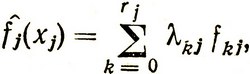
(2.22)
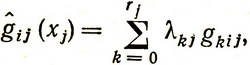
(2.23)
где fkj = fj (xkj) и gkij = gij (xkj) - фиксированные числа,
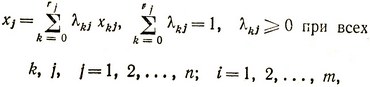
причем для данного j не более двух соседних λkj могут быть положительными. Отметим, что при построении функций 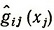 и
и 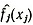 используется одно и то же разбиение интервала c1j<xj<c2j, на котором точки xkj по условию выбираются так, чтобы обеспечить удовлетворительную точность аппроксимации всех функций fj (xj) и gij (xj).
используется одно и то же разбиение интервала c1j<xj<c2j, на котором точки xkj по условию выбираются так, чтобы обеспечить удовлетворительную точность аппроксимации всех функций fj (xj) и gij (xj).
Подстановка выражений (2.22) и (2.23) в (2.21) позволяет получить форму записи приближенной задачи, отличающуюся от (2.21) тем, что вместо переменных xj используются переменные λkj
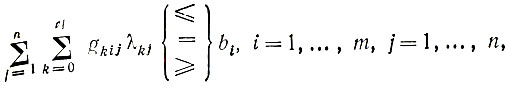
(2.24)
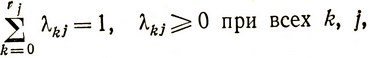
найти минимум (максимум) 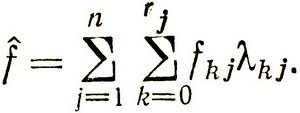 Таким образом, задача с сепарабельными функциями сведена к задаче линейного программирования. Далее можно искать решение этой задачи с помощью симплексного метода. Причем если функции fj (xj) выпуклые (вогнутые) и gij (xj) обладают свойствами, при которых множество допустимых решений выпукло, то при решении приближенной задачи как задачи линейного программирования получается оптимальное решение даже в том случае, когда при построении базиса не учитывается требование того, чтобы при каждом j не более двух соседних λkj были положительны. Доказательство этого положения можно найти в более подробных курсах нелинейного программирования [8].
Таким образом, задача с сепарабельными функциями сведена к задаче линейного программирования. Далее можно искать решение этой задачи с помощью симплексного метода. Причем если функции fj (xj) выпуклые (вогнутые) и gij (xj) обладают свойствами, при которых множество допустимых решений выпукло, то при решении приближенной задачи как задачи линейного программирования получается оптимальное решение даже в том случае, когда при построении базиса не учитывается требование того, чтобы при каждом j не более двух соседних λkj были положительны. Доказательство этого положения можно найти в более подробных курсах нелинейного программирования [8].
Следует, однако, иметь в виду то обстоятельство, что задача вида (2.9) - (2.10) даже небольшой размерности может свестись к задаче (2.24) очень большой размерности. Поэтому может оказаться выгодным вначале решать задачу при довольно грубом разбиении интервала изменения переменных, а затем уточнять результат, используя более мелкое разбиение в окрестности полученного грубого решения. При этом если некоторая переменная xj входит в задачу линейно, т. е. gij (xj) = aijxj и fj (xj) = cjxj, то нет необходимости выражать xj через λkj, а можно просто использовать xj как переменную. Это обстоятельство позволяет уменьшить размерность задачи.
Проиллюстрируем описанный выше метод приближенного решения задачи с сепарабельными функциями на следующем примере, который позволит также продемонстрировать экономические аспекты, возникающие при переходе от линейных задач к нелинейным.
Возьмем за основу линейную задачу, решенную ранее (см. гл. I, § 5, п. 3). В этой задаче мы предполагали все aij и cj заданными числами, что очень грубо отражает действительное положение, складывающееся на практике. Обычно в производстве всегда имеется возможность появления брака, т. е. расходования ресурсов без выпуска изделий. Процент брака может не быть постоянной величиной; например, он может увеличиваться о ростом интенсивности производства.
Допустим, что специальные исследования, проведенные на данном предприятии, показали, что зависимости себестоимости от объема производства изделий в первом приближении могут считаться линейными функциями, т. е. Cj = cj0 + cj1xj (все cj0≥0, cj1≥0, j = 1, 2), и из-за наличия брака расход ресурсов на изготовление изделий также в первом приближении линейно зависит от объема производства этих изделий (все в расчете на тысячу штук);
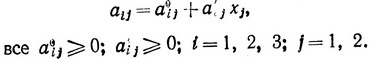
Подставляя Cj и aij в условия линейной задачи, приходим к следующей нелинейной задаче;
найти
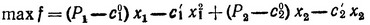
при ограничениях
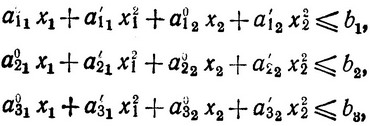
или в сокращенной записи;
найти
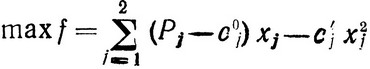
(2.25)
при ограничениях
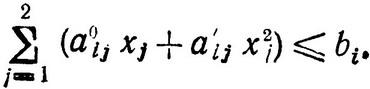
Сравнивая задачи (2.25) и (2.9)-(2.10), нетрудно видеть, что в нашем примере
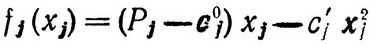
и
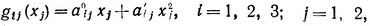
т е. мы пришли к нелинейной задаче с сепарабельными функциями. Этот пример является иллюстрацией приведенного в самом начале данной главы утверждения, что попытка более детального рассмотрения линейных задач почти все-а приводит к нелинейности.
Проверим, обладают ли функции fj (xj) и gij (xj) задачи (2.25) свойствами выпуклости или вогнутости. В данном случае достаточно убедиться в том, что любая из функций fj (xj) и gij (xj) обладает этим свойством. Возьмем, например, функцию f1 (x1) = (P1 - c01)x1 - c11x21 и составим для нее неравенство (2.4). Для этого выберем две произвольные точки x11 и x12 и определим при любом 0≤λ≤1 значение функции
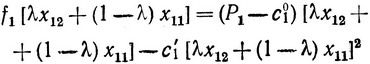
и сумму
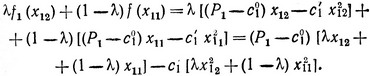
Как и следовало ожидать, линейные слагаемые этих выражений совпадают, и поэтому необходимо сравнить по величине только нелинейные слагаемые. В результате простых преобразований получаем:
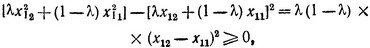
так как все сомножители λ, (1-λ) и (x12 - x11)2 неотрицательные числа. Функция f1 (x1) - вогнутая, поскольку
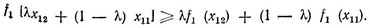
Совершенно аналогично доказывается выпуклость функции gij (xj). Итак, задача (2.25) является задачей выпуклого программирования. Перейдем к приближенному решению этой задачи.
Прежде всего определим максимальные значения переменных x1 и x2. Для этого сначала в ограничениях положим x2 = 0, решим три получившихся квадратных уравнения относительно x1 и выберем из этих решений минимальное: I
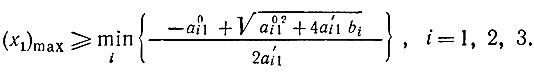
Знак "-" перед корнем в решениях не учитываем, так как по условию x1≥0. Аналогично имеем
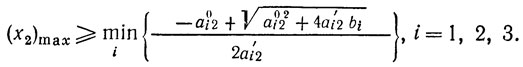
Обозначим эти значения следующим образом: (x1)max = α и (x2)max = β. Таким образом, переменные x1 и x2 могут изменяться в интервалах 0≤x1≤α, 0≤x2≤β. Разобьем первый из этих интервалов, например, на пять одинаковых отрезков точками x01 = 0, x11, x21, x31, x41, x51 = α и второй - точками x02 = 0, x12, x22, x32, x42, x52 = β. Соответственно координаты точек внутри интервалов есть
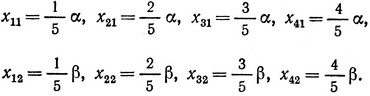
Не представляет труда непосредственно убедиться в том, что любое значение x1 из интервала (0, α) может быть получено с помощью выражения
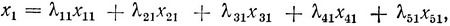
где все 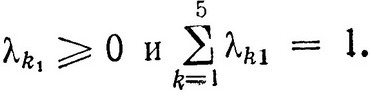
То же самое можно сказать и о x2. Тогда кусочно-линейные функции 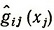 и fj (xj) запишутся в следующем виде:
и fj (xj) запишутся в следующем виде:
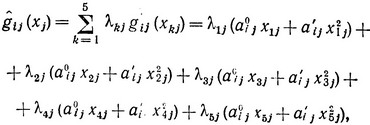
(2.26)
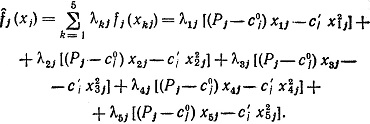
Функции 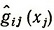 и
и 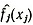 - линейные функции переменных λkj, так как все выражения в скобках - заданные постоянные числа. Таким Образом, от нелинейной задачи 2.25) путем линейной аппроксимации мы перешли к следующей линейной задаче:
- линейные функции переменных λkj, так как все выражения в скобках - заданные постоянные числа. Таким Образом, от нелинейной задачи 2.25) путем линейной аппроксимации мы перешли к следующей линейной задаче:
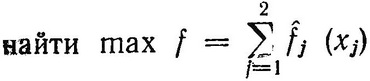
при ограничениях
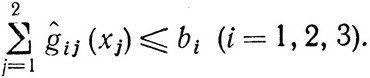
(2.27)
Далее линейная задача (2.27) может решаться симплексным методом, причем без учета ограничительных условий на выбор λkj, так как мы показали, что задача (2.25) является задачей выпуклого программирования.
Проиллюстрируем решение этой задачи на конкретном примере. Используем те же численные условия, что и в лисиной задаче, и дополнительно будем считать, что все a'ij = 1 и c'j = 0,1.
При этих условиях задача имеет вид:
найти max f = 2x1 - 0,1x12 + 3x2 - 0,1x22
при ограничениях
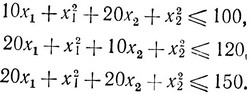
Решая квадратные уравнения
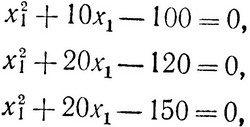
находим (x1)max≥min (6, 2; 4,9; 5,8} = 4,9.
Аналогично имеем (x2)max≥min {4, 2; 7; 5,8} = 4,2. Для удобства расчетов примем, что оба переменных изменяются в интервале (0;5), который и разобьем на 5 отрезков единичной длины, т. е. имеем:
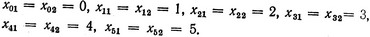
Запишем функции 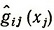 и
и 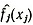 :
:
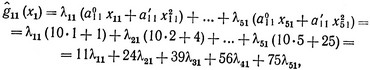
и аналогично
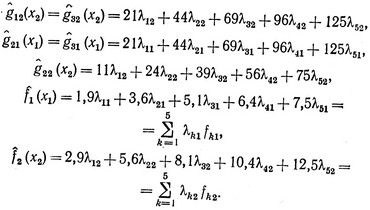
Подставляя эти линейные функции в условия задачи (2.27), мы приходим к задаче линейного программирования вида (2.24) с тремя ограничениями и тринадцатью неизвестными (с учетом искусственных переменных), которая далее может решаться с помощью стандартной процедуры симплексного метода, описанной в § 5 гл. I. Оптимальное решение находится после того, как получены значения λkj:
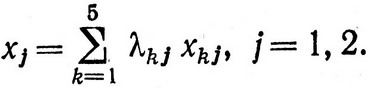
При этом значение функции цели есть
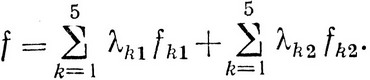
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'