§ 4. Задачи с сепарабельными функциями

Будем, например, искать решение задачи следующего вида:

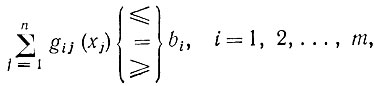
(2.9)

которое обращает в минимум (максимум) целевую функцию

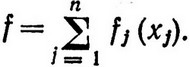
(2.10)

Здесь все функции в ограничениях и целевая функция являются сепарабельными.

Решение этой задачи может быть получено приближенными методами, в основу которых положена кусочно-линейная аппроксимация функций g_ij (x_j) и f_j (X_j) (см. [8]). В результате мы приходим к приближенной задаче, которая может быть решена симплексным методом. В случае, когда функции g_ij (X_j) обладают соответствующими свойствами выпуклости или вогнутости и f_j (X_j) являются выпуклыми (вогнутыми), решение приближенной задачи дает абсолютный минимум (максимум), который в принципе может быть сделан сколь угодно близким к абсолютному минимуму (максимуму) исходной задачи. Множество М допустимых решений, определяемое выражением (2.9), является выпуклым в следующих случаях: 1) в ограничениях со знаком "≥" все g_ij (x_J) - вогнутые функции; 2) в ограничениях со знаком "≤" все g_ij (x_j) - выпуклые функции; 3) в ограничениях, входящих только со знаком "=", все g_ij (x_j) - линейные функции. Эти правила следуют из определений выпуклого множества (см. п. 2, гл. I, § 3), выпуклой и вогнутой функций (§ 3, гл. II).

Существует ряд практических приемов сведения исходной задачи к виду (2.9) - (2.10), основанных на введении новых переменных.

Пусть, например, в качестве слагаемого в ограничениях или в функции цели имеется произведение x_ix_j, в результате чего эти функции не являются сепарабельными. Введем новые переменные y_i и y_j следующим образом:

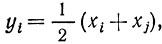
(2.11)

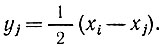
(2.11)

Тогда x_ix_j = y_i² - y_j², и в новых переменных соответствующая функция приобретает сепарабельную форму. При этом в условие задачи включаются два дополнительных ограничения вида (2.11). Таким образом, каждый раз при исключении произведения x_ix_j приходится расширять задачу включением дополнительных ограничений.

Если в качестве слагаемого содержится произведение двух или большего числа переменных, то при условии, что все переменные строго положительны, можно применить следующий прием. Введем (для случая произведения двух переменных) новую переменную

и прологарифмируем это выражение:

Далее вводим новую переменную (2.12) и выражение (2.13) в задачу. Очевидно, требование строгой положительности переменных x_i и x_j позволяет избежать трудностей, которые возникнут из-за того, что lg 0 = -∞.

Можно, однако, модифицировать этот прием таким образом, чтобы он стал пригоден для любых неотрицательных x_i и x_j. Введем новые переменные z_i и z_j и некоторые фиксированные положительные числа d_i и d_j таким образом, чтобы

Тогда z_i≥d_i>0, z_j≥d_j>0 и x_ix_j = z_iz_j - d_iz_j - d_jz_j + d_id_j.

Теперь можно ввести переменную y = z_iz_j и записать

Вместо произведения x_i*x_j вводим в задачу новые переменные y, z_i, z_j и добавляем три новых ограничения (2.14) и (2.15). Этот метод в принципе может быть обобщен на случай произведения любого числа переменных.

С помощью логарифмирования легко преобразовать к сепарабельному виду выражения, содержащие экспоненты, например, e^(ax_i2+bx_j), введя новую переменную y:

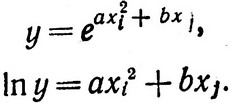
(2.16)

Аналогично при наличии в задаче членов вида x_i^x_j производим замену следующих переменных (при x_i>1, x_j≤0):

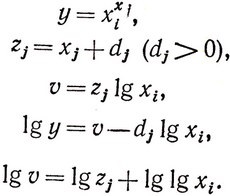
(2.17)

Представленные приемы показывают, что к сепарабельной форме можно привести задачи весьма различные в своей первоначальной постановке. Благодаря этому довольно широкий круг практических задач может решаться на основе методов, разработанных для решения задачи вида (2.9)-(2.10). Однако, если в задаче много функций, не имеющих сепарабельной формы, размерность приведенной задачи может становиться очень большой из-за большого числа новых ограничений, возникающих во время приведения исходной задачи к сепарабельному виду.