
Глава II. Выпуклое программирование
§ 1. Нелинейное и выпуклое программирование
Большое число практических экономических ситуаций, исследование которых является предметом математического программирования, либо вообще не может быть сведено к линейным задачам, либо (даже когда такая линеаризация на каком-то этапе производится) попытка более детального рассмотрения все же приводит к нелинейности.
Наиболее общая задача нелинейного программирования может быть сформулирована следующим образом:
требуется определить значения n переменных x1, x2, ..., xn, которые удовлетворяют m уравнениям или неравенствам вида
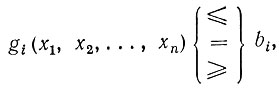
(2.1)
i = 1, 2, ..., m.
и обращают в максимум (или минимум) функцию цели
f (X) = f (x1, x2, ..., xn).(2.2)
Предположим, что f и gi - нелинейные заданные функции, bi - известные константы. Обычно считается, что все или по крайней мере некоторые переменные должны быть неотрицательными.
В частном случае линейного программирования предполагается, что функции f и gi являются линейными, т. е.
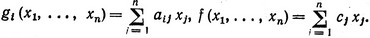
Всякая другая задача математического программирования, отличная от этой, считается нелинейной задачей.
В соответствующих разделах математики разработаны общие (классические) методы определения максимумов и минимумов функций различного вида. Однако такой общий подход к решению задач практически находит ограниченное применение для получения численных результатов, поскольку приводит к необходимости решать нелинейные системы уравнений со многими неизвестными и не годится для нахождения краевых экстремумов. Поэтому в математическом программировании в основном изучаются методы, которые могут служить алгоритмом, т. е. вычислительной процедурой при численном решении специальных задач, имеющих конкретные экономические приложения. Укажем некоторые из таких задач.
Наиболее основательно изучены задачи с линейными ограничениями и нелинейной функцией цели. Однако даже для этих задач вычислительные методы разработаны лишь в случаях, когда функция цели обладает определенными свойствами. В частности, например, функция цели может быть представлена в виде
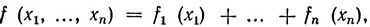
где на функции fj (xj) должны в свою очередь быть наложены некоторые ограничения. Это так называемая сепарабельная функция. В другом случае целевая функция может быть записана как сумма линейной и квадратичной функций:
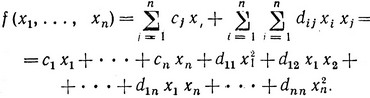
Нелинейные задачи такого типа называются задачами квадратичного программирования. Для того чтобы найти оптимальное решение, на величины dij необходимо наложить некоторые дополнительные ограничения.
Задачи с нелинейными ограничениями более трудны, чем с линейными. Чтобы в этих задачах получить оптимальное решение, к функциям gi и f должны быть предъявлены весьма жесткие требования. В частности, оптимальное решение нелинейной задачи может быть получено в том случае, если ограничения gi, заданные нелинейными неравенствами, определяют выпуклое множество в пространстве Переменных (см. гл. 1, § 3) и функция цели является нелинейной гладкой выпуклой или вогнутой функцией. В дальнейшем будет дано строгое определение выпуклой и вогнутой функций. Здесь же только необходимо указать, что свойство выпуклости функций f обеспечивает существование лишь одного минимума, а свойство вогнутости f - лишь одного максимума f внутри области, задаваемой ограничениями. На этом и строятся алгоритмы определения оптимального значения функции цели. При отсутствии выпуклости или вогнутости решение задачи математического программирования наталкивается на наличие локальных минимумов или максимумов, к отысканию которых в общем случае применимы классические методы.
Таким образом, свойство выпуклости (вогнутости) функции цели является важным свойством, гарантирующим получение соответствующего оптимального решения нелинейной задачи. Выпуклым программированием называется раздел математического программирования, в котором изучаются методы отыскания минимума выпуклой или максимума вогнутой функции на выпуклом множестве.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'