
§ 2. Относительный и абсолютный максимумы и минимумы функции
Говорят, что функция f (X), определенная на некотором множестве М, достигает на нем относительного максимума в точке X0, если найдется некоторое число δ, такое, что для всех X из М, удовлетворяющих условию 0<|X - X0|<δ, справедливо неравенство f(X)≤f(X0). Если выполняется строгое неравенство, то такой максимум называется строгим относительным максимумом. Здесь через X обозначается точка с координатами x1, x2, ..., xn, через X0 - точка x01, x02, ..., x0n.
Если функция f (X) в некоторой точке X* множества М достигает максимума и, кроме того, для любой точки X из М имеет место f (X) ≤ f (X*), то такой максимум называется абсолютным, или глобальным, максимумом. Если множество М замкнутое ограниченное, а функция f непрерывна на этом множестве, то абсолютный максимум функции f обязательно достигается по крайней мере в одной точке множества М (подробнее см. [8]). Если множество М не ограничено, то абсолютный максимум может и не достигаться ни в одной точке из М; однако он может оказаться равным предельному значению функции f при стремлении X к бесконечности.
Определения относительного и абсолютного минимумов получаются из соответствующих определений для максимумов заменой знаков неравенств на обратные. Отметим, что если функция f имеет в некоторой точке максимум, то функция -f имеет в этой же точке минимум.
Итак, если f (X) имеет в некоторой точке X0 из М максимум, то существует число δ такое, что для всех X из окрестности X0 имеет место неравенство f (X)≤f(X0). Возьмем точку X из этой δ-окрестности: X = X0 + Δxj, где |Δxj|<δ, Δxj - приращение j-й координаты, имеющее вид (0, ..., 0, Δxj, 0, ..., 0).
Тогда f (X0 + Δxj) - f (X0) ≤ 0 для всех Δxj или 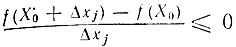 при Δxj>0, j = 1, 2, ..., n,
при Δxj>0, j = 1, 2, ..., n, 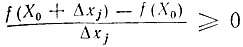 при Δxj<0.
при Δxj<0.
Переходя в этих неравенствах к пределу при Δxj→0, когда Δxj→ +0 и Δxj→-0 соответственно (т. е. при стремлении Δxj к нулю с разных сторон), и предполагая, что эти пределы существуют, получаем
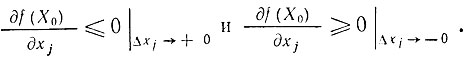
Очевидно, что если в точке X0 функция непрерывная и гладкая, то ее производные должны иметь определенное значение, т. е.
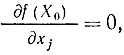
(2.3)
j = 1, 2, ..., n.
Так как аналогичные рассуждения можно провести для любого j, то это означает, что в точке X0 из М, где функция имеет максимум, все n частных производных функции f (X) Должны обращаться в нуль. Таким образом, для того чтобы найти координаты точек, в которых функция f максимальна, следует найти решение системы n уравнении вида ∂f/∂xj = 0, j = 1, 2, ..., n. Это общее свойство функций лежит в основе классических методов оптимизации.
Отыскание решения системы (2.3) может оказаться весьма трудной задачей, особенно если это решение не единственное. Поэтому для нахождения решения зачастую приходится пользоваться приближенными численными методами. Более того, система (2.3) может не иметь решения ни в одной точке ограниченного множества М, и тем не менее выпуклая (вогнутая) функция f (X) может достигать минимума (максимума) где-то на границе этого множества.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'