
§ 6. Двойственные задачи линейного программирования
Оказывается любой задаче линейного программирования можно поставить в соответствие другую задачу, сформулированную по определенным стандартным правилам таким образом, что решение любой из этих задач автоматически является решением другой задачи. Такие задачи называются взаимно двойственными.
Пусть, например, поставлена некоторая задача линейного программирования: из всех неотрицательных решений системы ограничений вида
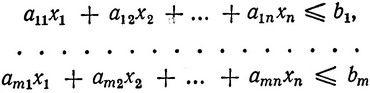
выбрать такое, которое максимизирует функцию цели f = c1x1 + c2x2 + ... + cnxn. Будем называть эту задачу прямой задачей. Сопоставим ей двойственную задачу: из всех неотрицательных решений системы

выбрать такое, которое минимизирует функцию цели
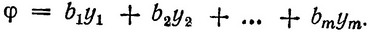
Двойственная задача получается из прямой задачи по следующим правилам:
- Свободные члены ограничений прямой задачи bi являются коэффициентами функции цели двойственной задачи, а коэффициенты функции цели прямой задачи становятся свободными членами ограничений двойственной задачи. Таким образом, число переменных в двойственной задаче равно m, т. е. числу ограничений прямой задачи, а число ограничений двойственной задачи равно n, т. е. числу переменных прямой задачи.
- Матрицей коэффициентов ограничений двойственной задачи служит матрица Aт, получаемая транспонированием матрицы A, составленной из коэффициентов ограничений прямой задачи.
- В системе ограничений двойственной задачи все неравенства меняются на противоположные, и требование достижения максимума f, имеющееся в постановке прямой задачи, заменяется в двойственной задаче на требование достижения минимума функции цели φ.
Нетрудно убедиться в том, что в качестве прямой задачи может быть использована двойственная задача и наоборот.
Тот факт, что решение прямой задачи является автоматически также решением двойственной задачи, следует из теоремы двойственности, которая формулируется следующим образом [18]:
если существуют решения прямой и двойственной систем, то значение функции цели f, соответствующее любому допустимому решению прямой системы, не больше значения функции цели φ, соответствующего любому допустимому решению двойственной системы; кроме того, для обеих систем существуют оптимальные допустимые решения, причем max f = min φ.
Мы не будем здесь приводить доказательства этой теоремы, отсылая интересующихся к более подробным курсам линейного программирования [1-3, 18]. Укажем только, что доказательство этой теоремы проводится при использовании симплексного метода.
Если по каким-либо причинам при решении задачи линейного программирования встретились трудности в вычислениях, то всегда можно составить для нее двойственную задачу и решать ее также с помощью симплексного метода. Такой способ решения прямой задачи называется двойственным симплексным методом (см. 12, 3, 5, 6). Этим методом выгодно пользоваться при решении на ЭВМ задач, в которых число ограничений значительно больше числа неизвестных, поскольку объем вычислений определяется в большей (степени числом ограничений, нежели числом неизвестных.
Отметим, что в то время как в обычном симплексном методе мы приближаемся к максимальному (минимальному) решению снизу (сверху), то в двойственном симплексном методе мы приближаемся к этому решению одновременно с противоположных сторон. Поэтому при решении некоторых задач о большим числом переменных и ограничений бывает удобно использовать для решения одной и той же задачи оба метода, так как при этом, подходя к оптимальному решению с противоположных сторон, можно прекратить вычисления, если разность между соответствующими функциями цели прямой и двойственной задач не превышает точности, требуемой при вычислении оптимального решения.
Зачастую наряду с прямой задачей двойственная задача линейного программирования может также иметь непосредственное экономическое истолкование. Например, если исходная задача заключается в установлении плана выпуска продукции, максимизирующего общий доход производства при заданных ограниченных ресурсах, то двойственная задача заключается в установлении оптимальных цен на Ходящие в состав исходного продукта компоненты, обеспечивающих необходимую сумму реализации от единицы продукции и минимизирующих стоимость производственных ресурсов. Более подробно этот вопрос разбирается в работах [5, 6, 18], где приведены также конкретные примеры.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'