Рассказ четырнадцатый. Что было дальше в теории экстремальных задач?

Рассмотрим простейшую задачу о максимуме и минимуме, указывающую нам путь естественного перехода от функций конечного числа переменных к величинам, зависящим от бесконечного числа переменных.

Г. Вольтерра

Излагаемые мною методы не требуют ни построений, ни геометрических или механических рассуждений. Они требуют только алгебраических операций, подчиненных планомерному и однообразному ходу.

Ж. Лагранж

Один старый французский математик сказал: "Математическую теорию только тогда можно считать совершенной, когда ты... берешься изложить ее содержание первому встречному".

Д. Гильберт

1. Об истории математического анализа. Развитие методов решения задач на максимум и минимум неразрывно связано с историей математического анализа. Мы касались этой темы неоднократно. Свяжем же теперь воедино многое из того, о чем рассказывалось раньше.

Сначала, как мы помним, задачи на максимум и минимум решались индивидуально и для каждой из них создавался свой собственный метод. В начале XVII века стала ощущаться потребность отыскать какие-то общие приемы исследования экстремальных задач. Попытки найти алгебраические способы отыскания максимумов и минимумов были сделаны Декартом. Ферма был первым, кто привлек для этих целей идеи, как мы скажем теперь, дифференциального исчисления. Свой метод он открыл, по его собственным словам, еще в 1629 году, но первое достаточно подробное изложение метода содержится в его письмах Робервалю и Декарту, которые он переслал в 1638 году.

"Все учение о нахождении наибольших и наименьших величин основывается на том, что... применяют следующее единственное правило", пишет Ферма и далее излагает суть своей теоремы, о которой говорилось в рассказе десятом.

Можно посоветовать читателю обратиться к книге Декарта "Геометрия" ([8], -с. 154), где приведено письмо Ферма, и осознать, как ему удалось выразить свой метод, не прибегая к понятию производной - ведь этого понятия тогда еще не было.

Свои теоретические выводы Ферма подкрепил примером: "Отрезок АС требуется разделить в Е так, чтобы прямоугольник со сторонами АЕ и ЕС был наибольшим (по площади)". Нетрудно усмотреть, что фактически это та же самая задача, которую поставил и геометрически решил Евклид в своих "Началах" (рассказ четвертый). Этот пример (причем в формулировке Ферма) был разобран в пятом рассказе.

В начале семидесятых годов XVII столетия Ньютон завершил свой труд под названием "Метод флюксий и бесконечных рядов с приложением его к геометрии кривых". Это сочинение было закончено к 1671 г., но опубликовано лишь в 1736 году. Имеется издание этой работы на русском языке [15].

В ней Ньютон закладывает начала дифференциального и интегрального исчисления, а также теории рядов. Разумеется, Ньютон уделил внимание и нахождению наибольших и наименьших величин. Мимоходом он упоминает прием Ферма, не называя, впрочем, его имени. Он пишет так: "найди флюксию (т. е. производную) и положи ее равной нулю" (в указ. соч. с. 73). Далее он решает два выразительных примера, где функция задана неявно и в одном из случаев - с иррациональностью. Затем он пишет: "С помощью метода решения этой проблемы можно получить решение следующих проблем" и указывает девять геометрических задач, которые он умеет исследовать. И снова первая среди них - задача, равносильная евклидовой.

В 1684 году появляется работа Лейбница, в которой также были заложены основания математического анализа. Уже само название ее, которое начинается со слов: "Новый метод нахождения наибольших и наименьших значений...", показывает, какую важную роль сыграла задача о нахождении экстремумов в становлении современной математики. В своей статье Лейбниц не только получает в качестве необходимого условия соотношение f' (х) =0, но и использует второй дифференциал для различения максимума и минимума (впрочем, это также было в то время уже известно Ньютону). С помощью соотношения f' (х) = 0 Лейбниц решает ряд конкретных задач, в частности выводит закон Снеллиуса (рассказ третий).

В трудах Лейбница, значительно опередивших свое время, уже прозвучала мысль о линейной аппроксимации функций, о связи производной и касательной. Эта идея претерпела затем интересную эволюцию, о которой будет рассказано в п. 5.

Исследования Ферма, Ньютона и Лейбница способствовали появлению метода отыскания экстремумов функций одного переменного. Казалось бы, естественно было начать изучение экстремумов функций двух переменных, трех переменных и т. п. Но этого не произошло. История анализа совершила своеобразный зигзаг и сразу стала изучать функции бесконечного числа переменных, и лишь через несколько десятилетий вернулась собственно к конечномерным задачам.

И в задаче Ньютона (рассказ восьмой), и в задаче о брахистохроне (рассказ седьмой), и в классической изопериметрической задаче (рассказ второй) испытанию подвергались "любые кривые". Их нельзя задать с помощью одного, двух, любого конечного числа параметров. В их "произволе" заключено "бесконечно большое число переменных". Недаром именно эти три задачи мы так и не смогли решить в нашем предыдущем рассказе.

С конца XVII века началась разработка теории задач, подобных этим трем. Было создано специальное "исчисление" этих задач. Оно оформилось в XVIII и XIX веках в трудах Эйлера, Лагранжа, Вейерштрасса и других. Его стали называть вариационным исчислением.

Несколько позже был развит анализ функций конечного числа переменных. А потом (и сравнительно недавно) было понято, что математический анализ бесконечного числа переменных не является принципиально более сложным, чем конечномерный анализ. И снова мысль о создании бесконечномерного анализа отталкивалась от потребности решать экстремальные задачи (см. слова Г. Вольтерра, поставленные нами в качестве эпиграфа, где Вольтерра имеет в виду классическую изопериметрическую задачу). Коснемся чуть подробнее темы:

2. Что такое функции бесконечного числа переменных? В рассказе девятом мы обсуждали вопрос: что такое функция? Сначала было рассказано о функциях одного переменного, когда одному числу х ставится в соответствие по определенному правилу чисто у. Затем речь шла о функции двух переменных, когда паре чисел (x₁, х₂) ставится в соответствие (и снова по определенному правилу) число y. Наконец, было сказано и о функциях n переменных. Но еще до девятого рассказа (и причем неоднократно) нам пришлось столкнуться с функциями бесконечного числа переменных, когда переменными были сами функции. (Вспомним формулу (2) в рассказе седьмом и формулу (8') в рассказе восьмом.) Такого рода функционалы (так зачастую называют в математике функции от функций) изучали почти за двести лет до того момента, как научились обращаться с функциями бесконечного числа переменных так же свободно, как и с функциями одного переменного.

Рассмотрим совокупность (в математике говорят еще - пространство) всех непрерывных функций на отрезке [а, b] числовой прямой. Ее обозначают С ([a, b]). Пусть эти непрерывные функции теперь играют роль аргумента. Попробуем осмыслить этот факт. Вспомним, что такое функция одного переменного, т. е. функция, заданная на числовой прямой R. (Скажем, все та же функция y = y(х) = √(1 + х²).) Это, как мы помним, - правило, дающее возможность по заданному числу х получать число у (в конкретном случае надо взять х, возвести его в квадрат, прибавить единицу и затем извлечь корень.)

Попробуем теперь понять, что такое функция F (у) на пространстве С ([а, b]). По самому смыслу понятия "функция" это должно быть некоторое правило, которое по непрерывной функции y(х), заданной на [а, b], дает возможность вычислить число F (y).

Возьмем несколько примеров. Для определенности пусть дальше а = 0, a b = 1.

Пример 1. F₁ (y) = 2y (0).

Что здесь предписано? По функции y (х) следует сначала вычислить то число, которое она принимает в точке нуль, а потом умножить его на 2. Вспомним несколько известных нам функций и вычислим для них значение, F₁ (y). Если y (х) = х, то y (0) = 0, и, значит, (y) = 0; если y (х) = √(1 + x²), то y(0) = 1 и F₁(y) = 2; если y(х) = √(1 + х²), то y (0) = 1 и F₁ (y) = 2; если y (х) = 5 × 2^х, то y (0) = 5 и F₁ (y) = 10.

Представьте себе теперь, что мы играем в такую игру: вам задают подряд несколько функций, а вы вычисляете F₁ (у) от каждой. К примеру, вам предлагают y (х) = 3 cos (х + 2), или 5ln(х + 3), или еще что-то. Мне кажется, вы не затруднитесь ответить, чему будет равно F₁ (y) в этих случаях. Понять правила этой игры - это и значит понять, что такое функция F₁.

Пример 2. F₂ (y) = ∫¹₀ y (х) dx. (Этот функционал выражает о не что иное, как площадь под графиком y(х).) И снова давайте играть в ту же игру. Я вам даю y(х) = 1 - вы мне вычисляете: F₂ (y) = 1; я вам - y (х) = х, вы мне - F₂ (y) = 1/2; я вам - y (х) = sin х, вы мне - F₂ (y) = 1 - cos 1 и т. д. Так мы познакомились с очень важным функционалом, функционалом площади.

Но можно придумать что-нибудь похитрее. Скажем,

Пример 3. F₃ (y) = (2_у (0))³ - (∫¹₀ y(х) dx)².

Здесь предписание более сложное. Если вам дают какую-то функцию y(х), то вы должны сначала вычислить y(0), затем это число умножить на два, потом полученное число возвести в куб, далее - найти интеграл от y (х) по отрезку [0, 1], возвести этот интеграл в квадрат, а затем из "куба" вычесть этот "квадрат". Скажем, если вам задали задачи y (х) = х, то получится - 1/4, а если y (х) = 5 × 2^х, то и вовсе придется потрудиться. Но важно, что "в принципе" вы выполните поставленную задачу и по каждой функции y (х) (которую можно отчетливо описать) получите число F₃ (y).

В рассказе девятом я писал в соответствующем месте: "А теперь давайте определим и изобразим несколько важнейших функций". Здесь что-либо изобразить трудно, ведь нужно рисовать в бесконечномерном пространстве, а "определить" - попробуем.

Простейшая функция - постоянная F (y) = с. Каждой непрерывной функции y(х) сопоставляется единственное число с.

Следующие по сложности функции - линейные. Что это значит - "линейная функция" от функции? Это значит, что сумму любых функций она переводит в сумму чисел (т. е. F (y₁ + y₂) = F(y 1) + F(y₂)) и, кроме того, что F (ay) = aF(y) для любого числа а и любой функции у(х).

Функции из примеров 1 и 2, приведенных нами выше,-линейные, функция из третьего примера линейной не является.

Здесь, в бесконечномерном случае, линейных функций очень много. (В каком-то смысле их даже "больше", чем всех непрерывных функций. Ведь если φ - непрерывная функция, то ей можно сопоставить линейный функционал

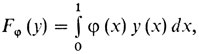
а функционал F₁ (y) = 2y (0) не может быть представлен в этом виде.)

Бесконечномерный анализ изучает функции от "бесконечного числа переменных", точнее - функционалы на бесконечномерных пространствах (типа пространства С ([а, b])). Приведем пример еще одного важного бесконечномерного пространства, с которым на протяжении двух веков в основном оперировало вариационное исчисление. Это пространство С¹ ([а, b]) непрерывно дифференцируемых функций y (х), т. е. таких функций y(х), которые сами непрерывны и их производные также непрерывны на отрезке [a, b].

В пространстве С¹ ([а, b]) определены функционалы, имеющие важный геометрический или физический смысл. Приведем примеры.

Пример 4 - функционал "длины":

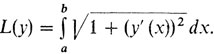
Пример 5 - функционал И. Бернулли - "время движения вдоль кривой" (см. формулу (2) в рассказе седьмом):

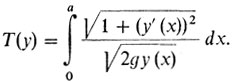
Пример 6 - функционал Ньютона - сопротивление движению в редкой среде (см. формулу (8') в рассказе восьмом):

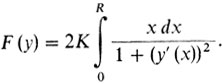
Эти примеры можно неограниченно продолжать. Но не будем делать этого, а перейдем сразу к вопросу о том, как ставятся экстремальные задачи для функционалов. В рассказе девятом говорилось: для того чтобы точно сформулировать экстремальную задачу, необходимо описать максимизируемую или минимизируемую функцию и ограничение. Ограничения, как мы помним, задаются обычно равенствами и неравенствами. В бесконечномерном случае все остается без изменений. Здесь также нужно описать минимизируемый и максимизируемый функционал (а значит, и пространство, на котором он определен) и ограничения.

Формализуем те задачи из первой части, которые мы не решали пока во второй. Во всех случаях будем исследовать задачи в пространстве С¹.

Задача Дидоны. Вспомним историю о Дидоне (начало второго рассказа). Анализируя ситуацию, в которой оказалась финикийская царевна, можно представить (среди прочих) следующие две возможности поставить задачу оптимизации.

А) Первая задача Дидоны, или классическая изопериметрическая задача. Требуется указать оптимальную форму участка земли, который при заданной длине периметра l имел бы наибольшую площадь.

Эта задача и исследовалась нами во втором рассказе. Другие постановки получаются, если, как это естественно считать, Дидона хотела сохранить выход к морю. Для простоты рассмотрим случай прямолинейного берега и будем при этом считать, что Дидоне были указаны границы, за пределы которых она не могла выйти (рис. 55).

Тогда получается

Б) Вторая задача Дидоны.

Требуется среди всех дуг длины l, лежащих в полуполосе 0 ≤ х ≤ a, y ≥ 0 с заданными концами в точках (0, 0) и (0, а), найти такую, которая вместе с отрезком y = 0, 0 ≤ х ≤ a ограничила бы фигуру наибольшей площади.

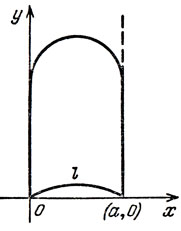
Рис. 55

Мы ограничим себя формализацией только второй задачи^*. Пусть y = y (х) - уравнение дуги. Выше нам встречались функционалы "площадь" и "длина".

Вспомнив, как они задаются, приходим к такой постановке:

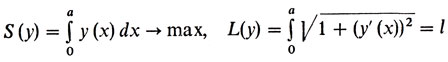
при граничных условиях y (0) = 0, y (а) = 0.

^* (Формализации первой задачи требуют рассмотрения функционалов от пары функций. Такого рода задачи мы опишем в конце этого рассказа. Решение же первой задачи нетрудно получить из решения второй.)

Максимизируемый функционал здесь - это площадь. Ограничение задается равенством L(y) = l, где L(y) - функционал длины. Граничные условия также задаются равенствами Γ₁ (y) = 0, Γ₂(y) = 0, где Γ₁ (y) = y (0), Γ₂(y) = y (а).

Задача о брахистохроне по сути дела была уже формализована нами. Вспомнив еще раз формулу (2) в рассказе седьмом, мы получим нужную формализацию:

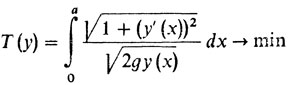
с граничными условиями y (0) = 0, y (а) = b.

Здесь минимизируемый функщюнал - это функционал Бернулли.

Задача Ньютона также фактически была формализована нами в восьмом рассказе. Эта формализация выглядит так:

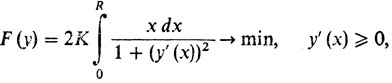
с граничными условиями у (0) = 0, у (R) = Я.

Обратим особое внимание на ограничение: y' (х) ≥ 0 - условие монотонности. Оно встретилось только здесь.

Напомним, что все эти задачи были решены нами по- разному (по крайней мере, внешне). Но во всех решениях присутствовало одно и то же: кривую мы всюду аппроксимировали ломаными и тем самым сводили задачу к конечномерной.

Такой метод решения задач подобного типа был осуществлен Эйлером, а его предшественником был, как мы помним, Лейбниц. Этот метод и его модификации получили название прямых методов в вариационном исчислении. Их и до сих пор применяют для численного решения задач вариационного исчисления.

3. Задачи вариационного исчисления и принцип Лагранжа для них. Мы много раз употребляли уже термин "вариационное исчисление", а теперь подошло время, чтобы его точно объяснить. Пусть нам задана некоторая, скажем, непрерывная функция трех переменных f(х, y, z). Рассмотрим следующий функционал:

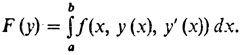
Этот функционал можно рассматривать в различных пространствах, но чаще всего его исследуют в пространстве С¹. Вариационным исчислением называется раздел теории экстремальных задач, где изучают максимумы и минимумы таких функционалов при различного рода ограничениях (о которых мы немного скажем дальше).

Посмотрим, что надо сделать, чтобы по функции y(х) из С¹ ([а, b]) получить число F (y). Сначала надо продифференцировать y (х). Затем надо подставить y(х) во второй аргумент, а y' (х) - в третий аргумент функции f(х, y, z). Тогда получится функция одного переменного, которая числу х ставит в соответствие число f(х, y (х), y' (х)). А в заключение надо взять интеграл от этой функции, и тогда получится искомое число F (y).

Вернемся на короткое время к двенадцатому рассказу. В первом пункте этого рассказа была поставлена задача о минимизации или максимизации функций нескольких переменных при ограничениях типа равенств и неравенств. Если бы неравенств не было, то задача приняла бы такой вид:

где х = (х₁ ,..., х_n) a F_i(x) функции n переменных (мы сознательно заменили малые буквы f_i большими F_i).

Давайте же теперь изучать точно такие же задачи, только здесь F_i - не функции многих переменных, а введенные выше функционалы типа F (y). Функционалы типа F (y) называют функционалами классического вариационного исчисления. Примеры их встретились y нас в предыдущих пунктах. Например, в функционале длины f (х, у, z) = √(1 + z²), в функционале площади f(х, у, z) = у, в функционале И. Бернулли f(х, у, z) = √(1 + z²)/√2gy и т. п.

Пусть далее задан набор функций f₀ (х, у, z), f₁ (х, у, z), ... ..., f_m (х, у, z). Рассмотрим соответствующие им функционалы вариационного исчисления F₀ (у), F₁ (у), ..., F_m (у) и следующую вариационную задачу:

где функции y(x) удовлетворяют краевым условиям на концах отрезка [а, b]: y (а) = у₀, y(b) = y₁.

Ее называют изопериметрической задачей классического вариационного исчисления.

Множество функций y(х) на С¹ ([a, b]), удовлетворяющих условиям Fi (у) = α_i, i = 1,..., m, y (a) = y₀, y(b) = y₁ называют допустимыми в задаче (з₁).

Если ограничения типа F_i (y) = α_i отсутствуют, то задача (з₁) принимает вид

по всем y(х) таким, что y(а) = y₀, y(b) = y₁ и задачу (з₂) называют простейшей задачей классического вариационного исчисления.

Задача о брахистохроне относится к числу простейших, вторая задача Дидоны - к числу изопериметрических (с этим и связан термин "изопериметрический" в применении к задаче (з₁)).

Задача Ньютона не относится ни к тому ни к другому типу, ибо там имеется дополнительное ограничение y'(х) ≥ 0 которого ни в (з₁) ни в (з₂) нет.

Возникает вопрос, как определить понятие локального минимума (максимума) в задаче (з₁). Для этого надо задать какую-то "меру близости" функций из С¹ ([а, b]) друг от друга. В качестве меры близости функции y(х) от функции, тождественно равной нулю, берут число

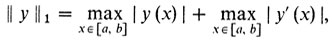
(его называют нормой функции y(х)), а в качестве меры близости функции y₁ (х) и y₂ (х) - число ||у₁ - y₂||. В пространстве С ([а, b]) норма вводится так:

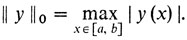
Теперь определение локального минимума становится совершенно аналогичным определению 1 из двенадцатого рассказа.

Определение. Говорят, что функция ŷ(х) доставляет локальный минимум (максимум) в задаче (з₁), если можно указать такое ε > 0, что для всех допустимых в задаче (з₁) функций, удовлетворяющих неравенству

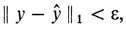
выполнено неравенство F₀ (у) ≥ F₀ (у̂) (F₀ (у) ≤ F₀ (ŷ)).

Возникает вопрос: как решать задачу (з₁)?

Напомним, в чем состоял принцип Лагранжа в применении к задаче (з). Он состоял из двух утверждений.

1) Для задачи без ограничений необходимым условием экстремума в точке х̂ является соотношение

(теорема Ферма).

2) Для решения задачи (з) надо составить функцию Лагранжа и затем поступить с ней так, как будто переменные независимы (т. е. нужно применить теорему Ферма). Второе утверждение мы назвали принципом Лагранжа.

В применении к задаче (з₁) все оказывается совершенно аналогичным. Только теорему Ферма требуется переосмыслить. Именно, имеет место следующая

Теорема (Эйлера). Пусть в простейшей задаче (з₂) f₀ - непрерывно дифференцируемая функция трех переменных. Тогда, если функция y(х) доставляет локальный экстремум (минимум или максимум) простейшей задаче (з₂), то удовлетворяется следующее уравнение:

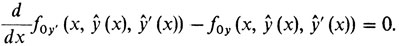(1)

Оно называется уравнением Эйлера задачи (з₂). Его допустимые решения называются стационарными точками задачи (з₂), или ее экстремалями.

Уравнение (1) и является расшифровкой уравнения типа F'₀ (х̂) = 0 в применении к простейшей задаче. Этот факт мы постараемся объяснить в следующем пункте. Отметим, что для решения конкретных задач не требуется понимания, откуда берется уравнение (1). Таким образом, алгоритм (идущий от Эйлера) исследования простейших задач состоит в следующем.

Нужно найти все решения уравнения (1) (а они зависят от двух параметров), которые проходят через данные точки, и выбрать среди них те, для которых функционал F₀ принимает наименьшее (наибольшее) значение.

Нетрудно показать непосредственным дифференцированием, что если f₀ не зависит от х, то уравнение (1) допускает следующее соотношение ("интеграл"):

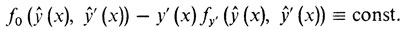(1')

Иначе говоря, любое решение уравнения (1) удовлетворяет соотношению (1').

Что же касается общей задачи (з₁) то к ней метод Лагранжа применим безо всяких изменений. Нужно составить функцию Лагранжа

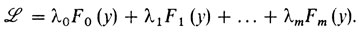
Ее можно записать так:

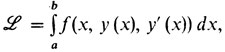
где

И далее следует поступать так, как будто мы имеем дело с нахождением экстремума функции L, а функции у не связаны. Иначе говоря, надо написать уравнение Эйлера

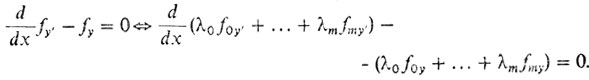
Все сказанное основывается ка следующей теореме.

Теорема (правило множителей Лагранжа для изопериметрических задач). Пусть функции f₀, непрерывно дифференцируемы. Тогда, если функция ŷ(х) достигнет локального экстремума (минимума или максимума) в задаче (з₁) найдутся числа λ₀ ,..., λ_m, не равные нулю одновременно и такие, что удовлетворяется уравнение Эйлера

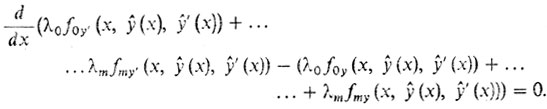(2)

Допустимые решения уравнения (2) называются стационарными решениями.

Правило множителей Лагранжа позволяет дать такой рецепт поиска решения задачи (з₁). Разбиваем его на те же 4 этапа.

1° Формализация задачи. 2° Применение принципа Лагранжа, т. е. составление уравнения (2) совместно с уравнениями F_i (у) = α_i и граничными условиями y (а) = у₀, y (b) = y₁. 3° Нахождение всех стационарных решений. 4° Отбор стационарных решений, являющихся решениями задачи.

Применим этот алгоритм к решению наших двух задач - о брахистохроне и Дидоны.

Решение задачи о брахистохроне.

1° Задача о брахистохроне была уже формализована нами как простейшая задача с

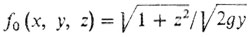
(не зависит от х).

2° Необходимое условие - уравнение Эйлера

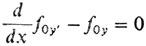
допускает интеграл

(*)

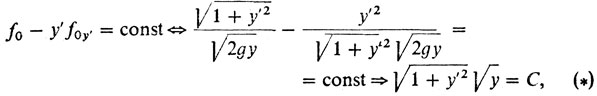где С - некоторая константа. Вспомним, что именно к этому соотношению и пришел сам И. Бернулли.

3° Нахождение стационарных точек - это нахождение решений уравнения (*). Но это уравнение было проинтегрировано нами. При этом оказалось, что решения его - это семейство циклоид.

4° В седьмом рассказе было показано, что имеется лишь одна допустимая циклоида из построенного в предыдущем пункте семейства. Она и будет решением задачи (это, конечно, еще нужно обосновать).

Решение второй задачи Дидоны.

1° Задача Дидоны была уже формализована нами как изопериметрическая задача с f₀ (х, у, z) = у, f₁ (х, у, z) = √(1 + z²).

2° Принцип Лагранжа. Составляем сумму f = λ₀f₀ + λ₁f₁ и выписываем уравнение Эйлера

(**)

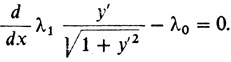3° Решаем полученное уравнение, учитывая, что если λ₀ = 0, то ŷ ≡ 0 (проверите, учтя граничные условия), что возможно, лишь если l = а. Значит, если l > a, можно считать, что λ₀ = 1. Тогда из (**) получаем

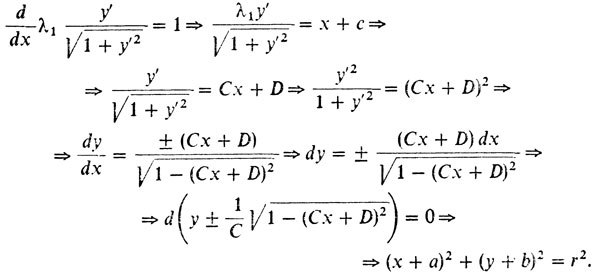
Получилось семейство всех окружностей.

4° Нетрудно теперь найти нужное решение. Если а < l ≤ πa/2, то в построенном семействе окажется единственная окружность длины l, проходящая через точки (0, 0) и (a, 0). Если же l > πa/2, то решением будет полуокружность с центром в точке (a/2, (l - πа/2)) радиуса а/2, "дополненная" отрезками х = 0, 0 ≤ y ≤ πа/ 2, х = а, 0 ≤ y ≤ l - πа/2 (см. рис. 55).

Отметим отличие наших решений в рассказе тринадцатом и здесь.

Там задачи были исследованы до конца. Здесь все-таки остается неопределенность, связанная с существованием решения. Существование решения в задачах вариационного исчисления доказывается труднее, чем в конечномерном случае. Более того, там часто решения просто не существует. Вот, например, в только что исследованной задаче Дидоны при l > πа/2 решения в обычном значении не существует, ибо поднятая полуокружность, "дополненная отрезками", не есть функция y(х), соединяющая точки (0, 0) и (a, 0).

Здесь, как говорят математики, имеется "обобщенное" решение.

Не так просто, как может показаться, обстоит дело и с брахистохроной, ибо циклоида не непрерывно дифференцируема, т. е., иначе говоря, решение задачи о брахистохроне не существует в той совокупности функций (в пространстве С¹ ([0, a])), в которой рассматривалась сама задача.

Знаменитому математику XX века Давиду Гильберту (его слова были поставлены эпиграфом к этому рассказу, и к ним мы еще вернемся) принадлежит идея о том, что любая естественно поставленная вариационная задача должна иметь решение, "если в случае необходимости самому понятию решения придать расширенное толкование".

И действительно, идея Гильберта оправдывается в большинстве задач, в частности в задаче о брахистохроне, задаче Дидоны, а также в двух задачах, которые были сформулированы в конце седьмого рассказа. К решению последних мы приступаем.

Задача Лопиталя. 1° Формализация. Время распространения света от точки (0, у₀) до точки (a, y₁) для среды, где скорость распространения зависит лишь от высоты y и равна υ(y), выражается интегралом

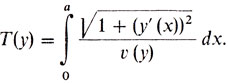
Для того чтобы убедиться в этом, нужно еще раз посмотреть на формулу (2) в рассказе седьмом. В итоге получается следующая простейшая задача классического вариационного исчисления:

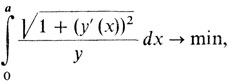
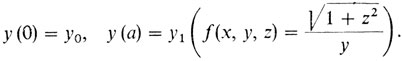
2° Необходимое условие - уравнение Эйлера. Оно допускает интеграл, который мы и выписываем:

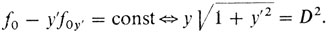
3° Найдем стационарные точки:

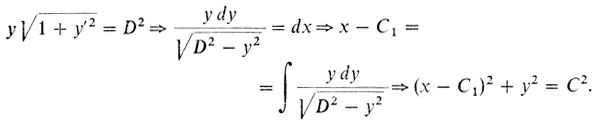
Уравнение Эйлера проинтегрировано. Получили семейство полуокружностей с центрами на оси Ох.

4° Легко понять, что через любые две точки (0, у₀) и (a, y₁) можно провести одну и только одну окружность нашего семейства. Эта окружность и будет решением задачи, но доказательство этого - за пределами наших возможностей. Те же самые полуокружности являются прямыми в интерпретации Пуанкаре плоскости Лобачевского.

Задача о минимальной поверхности вращения. 1° Формализация:

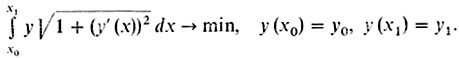
Вспомним: функционал "площадь поверхности вращения" уже выписывался нами в конце седьмого рассказа. Здесь был отброшен лишь множитель 2π. Таким образом, в рассматриваемом случае

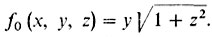
2° Необходимое условие - уравнение Эйлера, допускающее интеграл, который и выписывается:

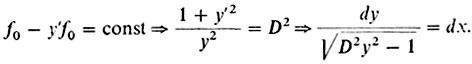
3° Нахождение стационарных точек (экстремалей). Решим уравнение из п. 2 с помощью подстановки:

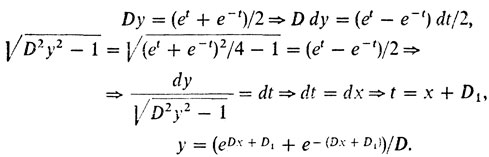
Кривая

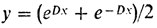
называется цепной линией.

4° Мы доказали, что если решение задачи о минимальной поверхности существует, то кривая вращения - это цепная линия.

Теперь снова вернемся к обсуждению идеи Гильберта об обобщенном решении. В задаче о брахистохроне и в задаче Лопиталя решение было найдено нами. Это не обобщенное решение, а "настоящее". Правда, и в том и в другом случае экстремали не являются непрерывно дифференцируемыми функциями, если ордината одной из концевых точек равна нулю. (Впрочем, в задаче Лопиталя из такой точки свет будет распространяться "бесконечное время", так что из физических соображений точки с ординатой нуль и рассматривать не нужно.)

В задаче Дидоны было найдено решение при l ≤ π/2 и обобщенное решение при l > π/2. В задаче о минимальной поверхности дело отстоит более сложным образом. Там иногда классическое решение существует, иногда - нет (см. рис. 56, где х₀ = - a, x₁ = a, y₁ = у₀). Если классического решения нет, то минимум доставляет обобщенное решение, состоящее из отрезков х = - а, 0 ≤ y ≤ у₀; х = а, 0 ≤ y ≤ y₁ и соединенных отрезком y = 0, -a ≤ x ≤ a (рис. 56,а). В этом случае "поверхность вращения" состоит из двух дисков, соединенных "перемычкой" y = 0, -а ≤ х ≤ а (рис. 56,б). В случае же, когда экстремаль существует, надо выбрать минимум из классического и обобщенного решений.

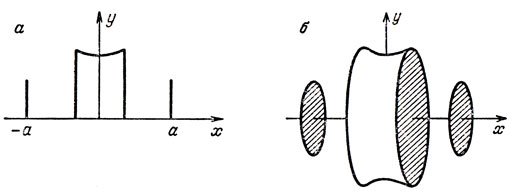
Рис. 56

4. Об истории вариационного исчисления. В предыдущем пункте мы объяснили содержание термина "вариационное исчисление". Теперь уместно рассказать об историческом развитии этого направления и о происхождении самого термина.

Все началось, как мы помним, с брахистохроны - задачи, поставленной Иоганном Бернулли в 1696 году. Эта задача привлекла всеобщее внимание, и вскоре было решено еще несколько подобных проблем. О некоторых упоминалось - вспомним минимальную поверхность вращения и задачу Лопиталя. И опять-таки для каждой задачи изыскивался свой способ исследования, хотя было ощущение, что возможен единый подход ко всем проблемам рассмотренного типа.

Тогда Иоганн Бернулли поставил перед своим учеником Леонардом Эйлером проблему изыскать общую методику решения всех этих задач. И Эйлер создал такой метод. В 1744 году вышел мемуар Эйлера, который так и назывался "Метод нахождения кривых линий, обладающих свойством максимума или минимума, или решение изопериметрической задачи, взятой в самом общем виде". Метод Эйлера состоял в том, что он нашел уравнение, которому должна удовлетворять "кривая линия, обладающая свойством максимума или минимума". Это уравнение уже было выписано нами. Его стали называть уравнением Эйлера.

Обратим внимание на слово "изопериметрический" в названии эйлеровского труда. С изопериметрической задачи мы качали нашу книгу. Какое же отношение она имеет к Эйлеру? Надо сказать, что Эйлер решил своим методом и классическую из оперим етрическую задачу. В других же многочисленных случаях, которые Эйлер сумел разобрать, ограничения не имели отношения к длине кривой, к ее периметру. Но в термине "изопериметрический" отразилась преемственность нашей науки, и с тех пор он закрепился.

Знаменательное событие произошло в 1759 году. Тогда совсем еще молодой Лагранж написал свое первое сочинение, касавшееся той же темы. Он подошел к ней с другой стороны и настолько удачно, что с тех пор метод Лагранжа (называемый иногда методом вариаций) стал общепринятым. Работа Лагранжа привела Эйлера в восхищение, и он отказался от публикации собственных разработок на эту тему, давая возможность молодому ученому самому довести свои замыслы до конца. Весь новый раздел математики Эйлер назвал "вариационным исчислением".

В чем же состоит метод Лагранжа? Что такое вариация?

Вернемся к п. 2 двенадцатого рассказа, где мы выводили конечномерную теорему Ферма. Напомним наши рассуждения.

Пусть y = f₀ (х) - функция n переменных х = (х₁,..., х_n). Предположим, что она дифференцируема и достигает локального экстремума в точке x̂. Тогда ясно, что функция одного переменного

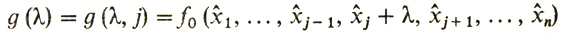
должна иметь минимум в нуле, и значит, по (одномерной) теореме Ферма должно иметь место равенство

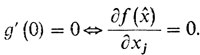
Лагранж в точности тот же прием применил к простейшей задаче классического вариационного исчисления:

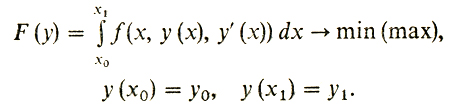(1)

Последуем за мыслью Лагранжа. Допустим, что функция f(х, у, z) в (1) непрерывно дифференцируема, а функционал F (у) достигает локального минимума на непрерывно дифференцируемой кривой у(х). Возьмем теперь "вариацию" у(х). Точнее, возьмем любую непрерывно дифференцируемую кривую у(х), которая обращается в нуль на концах: у (х₀) = у(х₁) = 0. Тогда "вариация" ŷ(х), т. е. добавка к ŷ(х) функции y (х), умноженной на любое число λ, не выводит нас из совокупности допустимых кривых - все они будут проходить через точки (х₀, y₀) и (x₁, y₁)- Следовательно, функция одного переменного

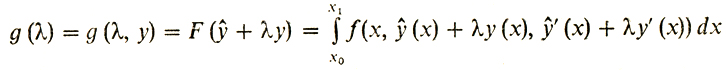
должна иметь локальный минимум в нуле, и значит, снова можно воспользоваться одномерной теоремой Ферма. Из этой теоремы вытекает, что g'(0) = 0. Теперь нужно вычислить g' (0). В анализе доказывается, что при наших допущениях о непрерывной дифференцируемости f(х, у, z) и у(х) возможно дифференцирование под знаком интеграла. Если проделать

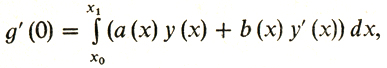(2)

где через а(х) обозначена функция -

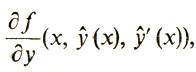
а через b(x) - функция

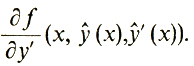
Итак, вслед за Лагранжем мы пришли к такому результату. Если ŷ(х) доставляет локальный минимум или максимум в простейшей задаче (1), то для любой непрерывно дифференцируемой функции y(х), если только она обращается в нуль на концах y(х₀) = y (x₁) = 0, выполнено равенство:

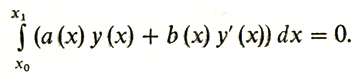
Продолжим рассуждение. Найдем такую функцию с (х), что

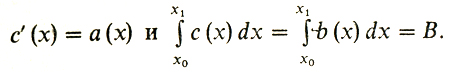
Для этого подберем константу D так, чтобы интеграл по отрезку [х₀, х₁] от функции

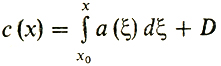
равнялся бы В. А теперь проинтегрируем первое слагаемое в (3) по частям:

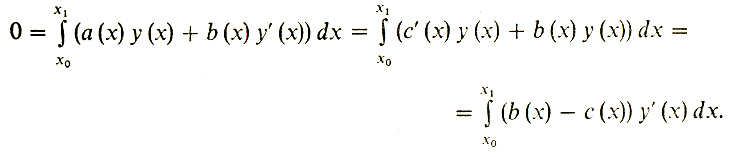
И, наконец, сделаем последний шаг. Положим

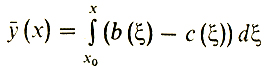
Тогда ясно, что ȳ (х₀) = 0. Кроме того,

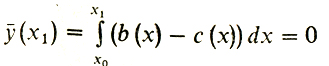
по построению функции с(х), откуда ȳ' (x) = b (х) - с (х). Это следует из формулы Ньютона - Лейбница. Значит, для ȳ(х) должно выполняться равенство (3), т. е.

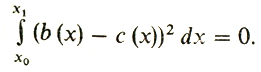
Но если непрерывная функция положительна, то ее интеграл не может равняться нулю. Значит, b(х) ≡ с (х), т. е. доказано, что

т. е.

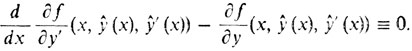(4)

Так выводится уравнение Эйлера по Лагранжу.

Вспомните: в предыдущем пункте этого рассказа говорилось, что уравнение Эйлера - это расшифровка теоремы Ферма для простейшей задачи. Здесь становится ясным смысл этого высказывания: уравнение Эйлера является следствием того, что "производная функционала F(y) в точке ŷ по любому направлению y(х) (y (х₀) = y(х₁) = 0) равна нулю". Отметим еще, что выражение для g'(0) получило название вариации функционала F.

Но Лагранж не остановился лишь на математических проблемах вариационного исчисления. Он, собственно говоря, и занимался-то ими лишь для того, чтобы иметь возможность применить их к проблемам естествознания. Главный труд его жизни - "Аналитическая механика" - книга о движениях тел в природе. В основе лагранжевого подхода к механике лежит экстремальный принцип, который называют принципом наименьшего действия. Проиллюстрируем его на простейшем примере.

Пусть шарик массы m подвешен (для простоты - в условиях невесомости) к пружине, для которой применим закон Гука о пропорциональности силы натяжения пружины ее отклонению от центра О. Чтобы впоследствии оставить уже введенные обозначения, мы подвесили пружину по оси Оу. Перемещение шарика тогда задает функцию y (t), где y (t) - его координата в момент t. Функция y(t) удовлетворяет, как известно, закону Ньютона

который гласит: "произведение массы на ускорение равно действующей силе" (ускорение - это вторая производная, а сила по закону Гука равна - ky (t), где k - коэффициент пропорциональности). Выражение T = m(y' (t))²/2 называется в механике кинетической энергией, U = ky²(t)/2 - потенциальной энергией, а интеграл от разности кинетической и потенциальной энергии называется действием. Рассмотрим задачу о минимизации действия при закрепленных граничных условиях:

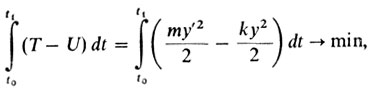(6)

Если написать уравнения Эйлера для задачи (6), то мы приходим к уравнению (5):

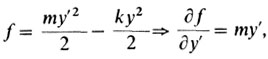
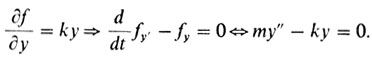
Таким образом, второй закон Ньютона - это не что иное, как уравнение Эйлера для действия. Или еще: истинные движения описываются стационарными точками действия. При малых временах истинная траектория и на самом деле минимизирует действие. Поэтому термин "принцип наименьшего действия" оказывается верным при малых временах. Вообще же правильнее говорить - "принцип стационарного действия".

И снова мы столкнулись с тем, что законы природы имеют двойное описание - "физическое" и "экстремальное", а впервые разговор об этом зашел у нас в третьем рассказе и был продолжен в седьмом. Там шла речь об оптике и минимизировалось время, здесь описываются движения тел и при этом минимизируется действие. В оптике нами рассматривались "волновые фронты", т. е. такие совокупности точек, куда свет приходит за одно и то же время. Якоби (вслед за Гамильтоном, который с этой точки зрения исследовал оптические явления) предложил рассматривать аналоги волновых фронтов и в задачах механики (рассматривая "фронты действия"), и вообще в любой простейшей задаче классического вариационного исчисления.

А именно Якоби начал рассматривать следующую функцию концевой точки S (х, у), равной значению интеграла

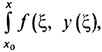
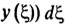
на экстремали (доставляющей минимум) и соединяющей фиксированную точку (х₀, y₀) с точкой (х, y).

Ясно, что любая часть экстремали, доставляющей минимум, является экстремалью, доставляющей минимум. Это простое соображение на самом деле является расшифровкой для общей ситуации принципа Гюйгенса в оптике (о котором мы говорили в третьем рассказе), и его тоже называют принципом Гюйгенса. Используя принцип Гюйгенса и уравнение Эйлера, нетрудно вывести уравнение, которому удовлетворяет функция S (х, у). Это уравнение называется уравнением Гамильтона - Якоби. Во многих интересных случаях его удается проинтегрировать, и этот метод дает еще одну возможность исследовать задачи классического вариационного исчисления. Таким образом, двойственность описания оптических явлений привела к двойному описанию решений любой задачи классического вариационного исчисления.

Вернемся несколько назад, в XVIII век. Для того чтобы можно было извлекать следствия из принципа наименьшего действия, необходимо было научиться решать задачи вариационного исчисления при ограничениях более сложных, чем изопериметрические, а именно требовалось исследовать задачи при связях, задаваемых дифференциальными уравнениями. Приведем одну общую постановку (восходящую к Лагранжу), к которой сводится большинство наиболее интересных задач из приложений. Пусть f_j = f_j (х, y₁, ..., y_n, z₁, ..., z_n), j = 0, 1, ..., k, k < n, функции 2n + 1 переменного. Рассмотрим задачу

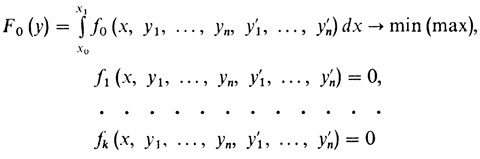
при граничных условиях y_i(х₀) = y_i0, y_i(x₁) = y_i1, i = 1,...,n

Эту задачу называют задачей Лагранжа. Как пишутся для нее необходимые условия экстремума?

Лагранж был уверен в том, что и эта задача должна подчиняться тому принципу о "снятии ограничений", который обсуждался в двенадцатом рассказе и был назван нами принципом Лагранжа. В соответствии с общим замыслом Лагранжа следует написать функцию Лагранжа и затем писать необходимое условие для задачи на экстремум функции Лагранжа при отсутствии ограничений. Но как же выглядит функция Лагранжа для задачи Лагранжа? И здесь снова Лагранж проявил максимальную решительность. В конечномерной задаче функция Лагранжа - это сумма функционала, умноженного на число λ₀, и произведений функций, задающих ограничения на множители Лагранжа. Но здесь, в задаче Лагранжа, имеется "столько же ограничений, сколько точек х на отрезке [х₀, x₁]", поэтому Лагранж и предложил умножать i-е уравнение f (x, y₁(x),...., y_n(x), y'₁(x),...., y'_n(x)) = 0 на функцию от х l_i(x), затем интегрировать по отрезку [х₀, x₁] и, наконец, суммировать по i. То есть Лагранж заменил умножение на числа и последующее суммирование умножением на функции и последующим интегрированием. В итоге функция Лагранжа приобрела следующий вид:

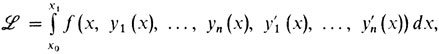
где

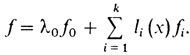
И он сформулировал следующий результат: если вектор-функция ŷ(х) = (ŷ₁(х),..., ŷ_n(х)) доставляет локальный минимум в задаче Лагранжа, то найдутся число λ₀ и функции l_i(х) такие, что для функции f выполнено уравнение Эйлера. (Лагранж, конечно, умножал функционал не на λ₀, а на единицу.)

Свой результат Лагранж не доказал. Впрочем, без каких бы то ни было ограничений сформулированный результат и не может быть верным. Так что и метод, легший в основу его величайшего труда - "Аналитической механики" - остался без строгого обоснования. Это продолжалось свыше ста лет. Теорема Лагранжа была доказана с полной строгостью лишь к концу XIX века, а суть этой теоремы была осознана лишь в нашем веке. А что это значит - "осознана лишь в нашем веке" - это предмет особого разговора, который и составит предмет следующего пункта.

5. Заключение. (Еще раз об истории математического анализа: бесконечномерный и выпуклый анализ; теория оптимального управления и принцип максимума Понтрягина; задача о быстродействии и задача Ньютона.)

Эта книга рассчитана на школьника. В первой части я избегал даже элементов математического анализа. Во второй мы говорили о вещах, которые не проходят в школе, например, о функциях нескольких и бесконечного числа переменных. Но все- таки пока мы не слишком удалялись от школьной программы. И в этом заключительном пункте моего заключительного математического рассказа - пятнадцатый рассказ будет посвящен общим вопросам и вольным разговорам - мне тоже не хочется отходить от своей установки писать "для первого встречного" (вспомним слова Гильберта) школьника. Но здесь мне хотелось бы обрести большую свободу и мысленно обратиться лишь к такому первому встречному школьнику, который уже принял решение связать свою судьбу с математикой. Я собираюсь говорить, как бы предвидя его будущее, в расчете на то, что он впоследствии самостоятельно заполнит неизбежные пробелы понимания, вызванные недостатком его теперешних знаний.

Мне представляется важным высказать и потом частично обосновать несколько общих тезисов касательно дальнейшей судьбы идей, обсуждавшихся раньше, при которой они, с одной стороны, возносятся ввысь, а с другой - возвращаются к своим истокам.

Вспомним: сначала Ферма (для полиномов), а затем Ньютон и Лейбниц в общей ситуации разработали метод исследования задач на максимум и минимум функций одного переменного. Далее сразу началась эра классического вариационного исчисления (И. Бернулли, Эйлер, Лагранж), когда стали исследовать экстремумы некоторых функций от бесконечного числа переменных. Она продолжалась примерно два с половиной века.

В конце XIX века Вольтерра и чуть позже - Фреше, Адамар и многие другие стали развивать основания бесконечномерного анализа. При этом всегда подчеркивалось, что одна из целей вновь, создаваемого исчисления - решать бесконечномерные задачи на максимум и минимум. Вспомним слова Вольтерра, поставленные эпиграфом к нашему рассказу. В первой половине нашего столетия математический анализ в бесконечномерных пространствах (его стали называть функциональным анализом, этот раздел анализа соединил в себе различные концепции классического анализа, высшей алгебры и геометрии) пережил пору бурного развития и расцвета. Однако математики, которые в это же время продолжали развивать вариационное исчисление, не прилагали общих теорем функционального анализа к вариационному исчислению и, более того, не считали, что разрабатывается аппарат для этой теории. Один из крупнейших специалистов в области вариационного исчисления в нашем веке - Блисс - в своем учебнике по вариационному исчислению, где он подвел итоги всего развития этой дисциплины, в книге, создававшейся в сороковые годы, когда все необходимые результаты функционального анализа уже стали общеизвестными, очень скептически отзывался о возможностях этого общего подхода в "конкретных" задачах вариационного исчисления.

И вот, пожалуй, теперь настало время сформулировать наш первый тезис.

Бесконечномерный анализ (точнее, дифференциальное исчисление в бесконечномерных пространствах) - это раздел математики, основанный в точности на тех же самых идеях, что и конечномерный, и столь же простой и естественный, как последний, является истинным аппаратом классического вариационного исчисления в той же мере, как конечномерный является аппаратом для теории конечномерных задач на экстремум. При этом все основные теоремы дифференциального исчисления в бесконечномерном пространстве столь же просты и естественны, как их конечномерные аналоги.

В основании дифференциального и интегрального исчисления для функций одного переменного лежат понятия производной и дифференциала. Вспомним их определение (рассказ одиннадцатый).

Мы говорили, что функция F(x), заданная на прямой R, дифференцируема в точке х₀, если существует такая линейная функция y = kx, что

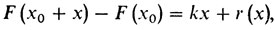
где

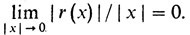
Линейная функция y = kx называется дифференциалом F в точке х₀.

Бесконечномерный анализ изучает функции на пространствах с нормой - так называемых нормированных пространствах. Примером нормированных пространств могут служить встретившиеся нам пространства С ([а, b]) и С¹ ([а, b]). А вообще нормированным пространством называется любая совокупность элементов Y таких, с которыми можно поступать так же, как с векторами на плоскости, т. е. складывать их и умножать на числа, а кроме того, таких, что каждому элементу y из Y приписано число ║y║, называемое нормой. Норма должна удовлетворять таким свойствам:

1) ║y║ ≥ 0 (не отрицательность) и ║y║ = 0, лишь если y = 0,

2) ║ay║ = |a|║y║ для любых y ∈ Y и a ∈ R (однородность).

3) 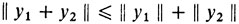Для всех y₁, y₂ из Y (аксиома треугольника).

Примерами нормированных пространств могут служить прямая R, где следует положить ║y║ = |y|, n-мерное пространство векторов y = (y₁, ..., y_n), где можно ввести нормы по-разному, например,

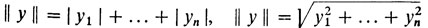
и т. п.,

а также встретившиеся нам пространства С и С¹.

Мы уже говорили, что функция K(y) называется линейной, если K(y₁ + y₂) = K (y₁) + K (y₂) для всех y₁, y₂ ∈ Y и K(ау) = аK(y) для любых y ∈ Y, a ∈ R.

Теперь можно определить понятие производной в любом случае.

Мы говорим, что функция F (y), заданная на нормированном пространстве Y, дифференцируема в точке у₀, если существует такая линейная функция K (y), что

где

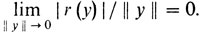
Линейная функция K(y) называется дифференциалом F в точке y₀.

Неправда ли, все очень похоже? Скажу больше. Определение дифференциала в бесконечномерном анализе дал французский математик Фреше в начале нашего века. Посмотрим, к чему приведет определение Фреше, если применить его к конечномерному случаю.

Мы скажем, что функция F(y) = F(y₁ ,..., y_n) n переменных дифференцируема в точке y₀ = (y₀₁,...,y_0n) если существует такая линейная функция (а любая такая функция имеет, как мы помним, вид K (у) = k₁y₁ + ...+ k_ny_n), что

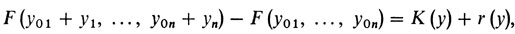
где

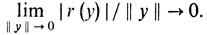
В качестве нормы можно взять любую норму в n-мерном пространстве. Сейчас именно это определение входит в каждый учебник по анализу. Но Фреше считал, что его придумал именно он! Он так и пишет: "дифференциал в моем смысле". Обычный конечномерный анализ существовал уже два с половиной столетия, и вместе с тем один из крупнейших математиков начала нашего века считает, что он впервые предлагает правильное определение основного понятия анализа - понятия дифференциала! Правда, потом выяснилось, что "его" определение уже было дано в неопубликованных трудах Вейерштрасса (относящихся к 60-м годам XIX века) и встречалось в английских и немецких учебниках начала века, но в научной литературе его действительно не было. Факт остается фактом - бесконечномерное определение оказалось легче придумать, чем конечномерное!

Далее. Какие теоремы дифференциального исчисления следует считать основными? Прежде всего необходимо назвать две теоремы - о дифференцировании сложной функции и об обратной функции.

Правило дифференцирования сложной функции (одного переменного) таково:

В бесконечномерном анализе эта формула также верна (если придать ей правильную трактовку) и доказывается столь же просто, как и в конечномерном.

Теорема об обратной функции (для одного переменного) гласит: если непрерывно дифференцируемая функция y = f(х) равна нулю в точке 0 и при этом f'(0) ≠ 0, то вблизи нуля функцию f можно обратить, т. е. для любого достаточно малого ȳ найдется такое единственное х̄, что ȳ = f(х̄).

Как доказывается эта теорема? Среди разнообразных доказательств ее отдадим предпочтение доказательству, восходящему к Ньютону. Оно состоит в построении последовательности {х_n}_n≥0, постепенно сходящейся к х̄. Эта последовательность строится по правилу:

а геометрически она изображена на рис. 57. Нулевое приближение х₀ берется произвольно в достаточной близости от нуля.

В бесконечномерном случае верен тот же результат. Рискну сформулировать его. Одной нормированности здесь недостаточно. Нужно еще одно свойство, так называемое свойство

полноты, "отсутствия пробелов" (рациональные числа не образуют полного пространства, ибо между ними имеются "пробелы" типа числа √2, которое не рационально). Полные нормированные пространства называются банаховыми.

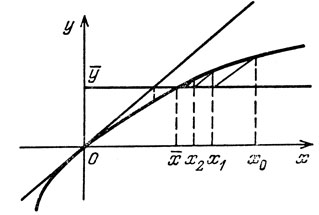
Рис. 57

Пусть теперь X и Y - два банаховых пространства и F - Функция, отображающая X в Y. Производная ее - это линейное непрерывное отображение, переводящее X в Y. Условие f'(0)≠ 0 в одномерной теореме на наш "бесконечномерный язык" переводится так: производная F'(0) обратима (т. е. (F(0))^-1 является также линейным и непрерывным отображением из Y в X). И теперь теорема об обратной функции получает совершенно аналогичный вид: если X и Y - банаховы пространства и непрерывно дифференцируемая функция y = F (x) равна нулю в нуле и F' (0) - обратима, то для любого ȳ, близкого к нулю, найдется такое единственное х̄, что F (х̄) = ȳ.

И доказательство фактически никак не меняется: доказательство сходимости х_k, определенных по формуле (1), к x̄ проводится совершенно аналогично тому, как на прямой R.

Подведем итоги. И основное понятие - понятие дифференциала, и формулировки основных теорем, и их смысл, и их доказательства в одномерном и бесконечномерном случае фактически одинаковы. При этом.

В бесконечномерном анализе верен принцип Лагранжа, причем основания для него те же, что в конечномерном случае, и доказательства столь же просты.

Пусть снова X и Y - банаховы пространства, f_i - функционалы на X, i = 0, 1, ..., m, a F - отображение из X в Y Рассмотрим задачу

Если отображение F и функции f отсутствуют, то получается задача без ограничений:

В применении к задаче (з) принцип Лагранжа формулируется с употреблением тех же слов, что употребляются и в конечномерном случае, и для изопериметрических задач классического вариационного исчисления, а именно:

1) Для задачи (з') необходимым условием экстремальности является соотношение

(теорема Ферма).

2) Для решения задачи (з) надо составить функцию Лагранжа задачи и затем поступить с ней так, как будто переменные независимы.

Функция же Лагранжа задачи (з) имеет стандартный вид

где λ₀, ..., λ_m - числа, а Λ(y) - линейная функция на Y.

Таким образом, если x̂ - локальный экстремум, то, найдутся такие числа λ₀, ..., λ_m и такая линейная функция Λ(y), что выполнена теорема Ферма для функции Лагранжа:

Но именно так и формулируется правило множителей Лагранжа в конечномерном случае - вспомним соответствующую теорему из двенадцатого рассказа. Сформулированную теорему о правиле множителей Лагранжа доказал в 1934 году советский математик Л. А. Люстерник.

При этом необходимо сказать, что в бесконечномерном случае, помимо гладкости входящих в постановку задачи функций и отображений (а ведь это было единственным требованием в конечномерном случае), нужны еще два требования.

Во-первых, нужно, чтобы пространства X и Y были полными, т. е. банаховыми, во-вторых, нужно, чтобы отображение F обладало бы некоторыми особыми свойствами, которые обычно называют свойствами регулярности (для регулярности и, следовательно, для того, чтобы было справедливо правило множителей Лагранжа, достаточно, чтобы производная F'(х) отображала X на все Y). Доказывается бесконечномерный результат столь же просто, как и конечномерный. Читателя, который пожелает в этом убедиться, я отсылаю к книге [2], где доказательство конечномерного случая приведено на с. 49 - 50, а бесконечномерного - на с. 254 - 255. Оба доказательства строго параллельны, только в нескольких местах некоторые известные результаты высшей алгебры и классического анализа заменяются их обобщениями в функциональном анализе (эти обобщения входят в самый минимум математического университетского образования).

А что же такое выпуклость и выпуклый анализ? С понятием выпуклости мы знакомимся в школе на уроках геометрии. Напомню: фигура на плоскости или в пространстве называется выпуклой, если вместе с двумя своими точками она содержит весь отрезок, соединяющий эти точки; функция называется выпуклой, если ее график лежит не выше хорды, соединяющей любые две точки графика. На рис. 45 изображены выпуклые и не выпуклые фигуры и функции. Треугольник - всегда выпуклое множество, а среди четырехугольников встречаются и не выпуклые. Линейные (y = ах, y = а₁х₁ + ... + a_nx_n) и аффинные (y = ах + b, y = a₁x₁ + .+ a_nx_n + b) функции являются выпуклыми; среди квадратных трехчленов y = ах² + bх + с, a ≠ 0, выпуклыми являются лишь те, у которых a > 0. Выпуклые Функции можно определить аналитически. Функция y = f(x) является выпуклой в том и только в том случае, если для любых точек x₁ и х₂ и любого числа α, лежащего между нулем и единицей, имеет место неравенство Иенсена

Это неравенство обобщается на случай n точек:

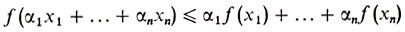
(если только

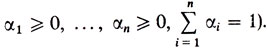
Вот важное достаточное условие выпуклости функции одного переменного: если функция f дважды дифференцируема и при этом f" (х) ≥ 0 для всех х, то она выпукла. Посмотрим теперь на функции из таблицы, приведенные в одиннадцатом рассказе. Легко понять, что функция y = |х| а выпукла тогда и только тогда, когда a ≥ 1, функция y = а^х (a > 0, а ≠ 1) всегда выпукла, выпуклой являются и функции y = log_ax, 0 <а < 1, y = -ln х. Функции y = sin х и y = cos х выпуклыми не являются.

Среди всех фигур выпуклые составляют лишь достаточно узкий, специальный класс. То же можно сказать и о выпуклых функциях. Однако выпуклость играет очень важную роль и в математике, и в ее приложениях. Содержательность идей, сопутствующих выпуклости, и богатство приложений привели к созданию отдельного раздела в математике, получившего название "Выпуклый анализ". Его окончательное оформление произошло сравнительно недавно - лет двадцать тому назад. В этом разделе изучают свойства выпуклых множеств, выпуклых функций и выпуклых экстремальных задач. Нас в основном будут интересовать, конечно, именно экстремальные задачи.

Надо сказать, что именно обилие выпуклых экстремальных задач привело к необходимости углубленного изучения выпуклости и в итоге - к созданию выпуклого анализа. Особенно много выпуклых задач возникает в экономике. Об одной задаче экономического содержания - транспортной задаче - мы говорили. Такого рода проблемы стали возникать постоянно. Очень часто при формализации таких задач выяснялось, что функции, которые требовалось максимизировать или минимизировать, а также функции, задающие ограничения (типа равенств и неравенств), являются линейными. Возник вопрос о том, как их решать. Методы их решения составили специальный раздел выпуклого анализа - линейное программирование. Первые работы, относящиеся к этому разделу, принадлежат советскому математику - академику, лауреату Ленинской и Нобелевской премий Л. В. Канторовичу.

Что же изучают в выпуклом анализе? Важный раздел выпуклого анализа составляет так называемое "выпуклое исчисление", имеющее много сходного с дифференциальным исчислением. Объясним, что это такое. Не все выпуклые функции дифференцируемы. Примером выпуклой функции, не дифференцируемой в нуле, является функция y = |х|.

Мы уже объясняли, что у этой функции нет (в нуле) касательной. Но у любой выпуклой функции y = f(х) одного переменного имеются две "полукасательные" (рис. 58).

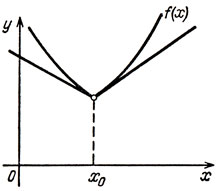
Рис. 58

Это означает, что всегда существуют пределы (далее h > 0)

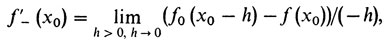
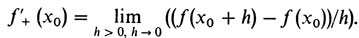
Весь отрезок

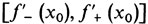
(как правило, вырождающийся в точку) называется субдифференциалом функции f в точке х₀. Он обозначается df (х₀). Если f - константа, то df (х) ≡ 0, если f (х) = ах + b, то df (х) = а в любой точке х. И вообще, если y = f(х) - функция, дифференцируемая в точке х, то df(х₀) = f'(x₀).

Если дифференцируемая функция имеет локальный минимум в точке х₀, то, как мы знаем, по теореме Ферма имеет место равенство f' (х₀) = 0. Мы отмечали при этом, что это равенство является необходимым, но не достаточным условием экстремума. Если функция выпукла, то ее локальный минимум всегда глобальный, абсолютный. В этом состоит одно из замечательных свойств выпуклых функций. Необходимым и достаточным условием минимальности выпуклой функции f в точке х₀ является соотношение 0 ∈ df(x₀) (теорема Ферма для выпуклых функций). Это соотношение означает совсем простую вещь: для того чтобы выпуклая функция f достигала минимума в нуле, необходимо и достаточно, чтобы постоянная функция, равная f(х₀), лежала бы ниже графика f.

Понятие субдифференциала можно обобщить и на случай функции n переменных. Субдифференциал, в отличие от производной, - это не вектор, а некоторое выпуклое множество векторов. При этом имеют место формулы, похожие на формулы дифференциального исчисления. Например, имеет место такая формула:

Она обобщает формулу (f + g) (х) = f' (х) + g' (х), о которой говорилось в одиннадцатом рассказе. Приведенная формула для субдифференциала суммы означает, что для того, чтобы узнать суб дифференциал функции f + g в точке х, надо взять множества А = df (х), В = dg (х) и образовать множество А + В из суммы а + b, а ∈ А, b ∈ В.

Соотношения, подобные формуле для субдифференциала суммы, и образуют выпуклое исчисление.

Важнейший тезис выпуклого анализа состоит в том, что выпуклые объекты всегда допускают двойное описание и что для выпуклого объекта всегда имеется "двойственный". Скажем, выпуклая фигура на плоскости может быть описана сама по себе как совокупность своих точек, а может быть описана также и как пересечение всех содержащих полуплоскостей (полупространств) (см., как на рис. 59 описывается треугольник).

Рис. 59

Аналогично всякая выпуклая функция может быть описана сама по себе, а также как максимум из всех аффинных функций, ее не превосходящих.

Это последнее двойственное описание приводит к одному из важнейших понятий всего классического анализа - понятию преобразования Лежандра.

Пусть y = f(х) - выпуклая функция. Преобразованием Лежандра ее называется функция

Приведем пример. Пусть

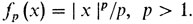
(При p > 1 функция y = f_p (х) является, как мы помним, выпуклой.) Для того чтобы найти шах (xz - f_p (х)), применим теорему Ферма.

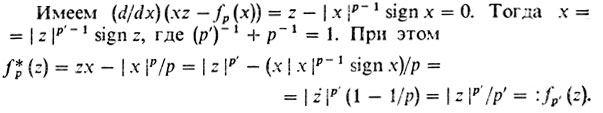
Таким образом, функции f_р(х) и f_р(х) двойственны: каждая из них является преобразованием Лежандра другой. При этом функция f₂ (х) = х²/2 является "самодвойственной".

В этом обстоятельстве лежит причина неравенств Коши - Буняковского и Гельдера, о которых говорилось в рассказе пятом. Отметим кстати, что большинство неравенств, исследовавшихся там, имеет отношение к выпуклому анализу. Например, неравенство между средним арифметическим и средним геометрическим есть не что иное, как неравенство Иенсена. Действительно, пусть x_i > 0, i = 1, ..., n. Тогда

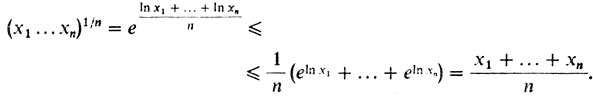
Мы воспользовались неравенством Иенсена для выпуклой функции y = e^х.

И еще один важнейший тезис выпуклого анализа. Рассмотрим треугольник ABC (см. рис. 60). Мы можем стереть все, кроме его вершин. Ведь зная вершины, мы восстановим весь треугольник. То же можно сказать относительно квадрата, ромба и вообще любого выпуклого многоугольника - они восстанавливаются по своим вершинам.

Рис. 60

Вершины многоугольника характеризуются тем, что они (в отличие от остальных точек многоугольника) не являются серединами каких-либо отрезков с концами в точках этого многоугольника.

Оказывается, у любого ограниченного (и замкнутого) выпуклого множества существуют "крайние" точки, т. е. такие точки, которые не могут оказаться серединами никаких отрезков, принадлежащих этому множеству. У круга, например, множеством крайних точек является ограничивающая его окружность. И при этом оказывается, что всякое выпуклое множество восстанавливается по своим крайним точкам.

Напомним, что задачи линейного программирования формализуются так:

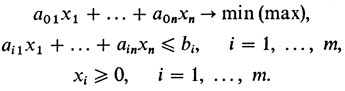
Ограничения в таких задачах образуют "многогранник", который восстанавливается по множеству своих вершин. При этом, как легко понять, минимум (или максимум) линейной функции достигается в одной из вершин.

Один из наиболее широко известных в мире численных методов (так называемый симплекс-метод) устроен так, что он дает возможность из некоторой вершины переходить в другую с меньшим (большим) значением минимизируемой (максимизируемой) функции. Через конечное число шагов находится нужный экстремум.

Теорию выпуклых экстремальных задач называют выпуклым программированием. Достаточно широкий класс конечномерных задач выпуклого программирования описывает следующая постановка:

По сравнению с той постановкой, которую мы привели в начале параграфа, здесь имеются следующие изменения. Во-первых, это задача на минимум, во-вторых, функция f₀ и функции, задающие неравенства, должны быть выпуклыми, в третьих, функции, задающие равенства, должны быть аффинными и, наконец; появилось еще одно ограничение: х ∈ А. При этом множество А также предполагается выпуклым. Вот в этом случае - для выпуклых задач - слова Лагранжа, сказанные о своем принципе и помещенные нами в эпиграф, полностью оправдываются, а именно имеет место следующая теорема.

Если допустимая точка x̂ доставляет абсолютный минимум в задаче (з') выпуклого программирования, то найдутся числа λ₀,...,λ_m не равные одновременно нулю и такие, что А) выполнены условия не отрицательности λ₀ ≥ 0, λ_i ≥ 0, i ≥ m' + 1, Б) выполнены условия дополняющей не жесткости λ_if_i(x̂) = 0, i ≥ т' + 1, и, наконец, В) имеет место так называемый принцип минимума, согласно которому точка x̂ является точкой минимума функции Лагранжа в задаче

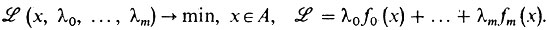
Если же оказалось, что нашлись такие числа λ₀,...,λ_m, и λ₀ = 1, что удовлетворяются соотношения А) - В), то x̂ является абсолютным минимумом в задаче.

Эта теорема была доказана сравнительно недавно - в 1951 году - американскими математиками Куном и Таккером. Она играет роль правила множителей Лагранжа для задач выпуклого программирования.

Закончим наш рассказ решением задачи Дидоны средствами выпуклого анализа.

Пусть A₁ и A₂ две выпуклые фигуры на плоскости. Через α₁А₁ + α₂А₂ обозначим фигуру, образованную векторами х, представимыми в виде х = α₁х₁ + α₂х₂, где х₁ из А₁, х₂ из А₂, α₁ ≥ 0, α₂ ≥ 0. Сумма многоугольника с кругом изображена на рис. 61.

Обозначим через S (А) площадь множества А. В середине прошлого века немецкий геометр Брунн доказал следующее важное неравенство:

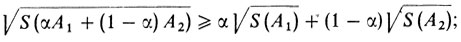(1)

затем в конце прошлого века Минковский доказал, что равенство в (1) возможно тогда и только тогда, когда А₁ и А₂ гомотетичны.

Рис. 61

Доказательство этих фактов и их обобщений, известны под названием неравенств Брунна - Минковского, можно найти в упоминавшейся нами книге Люстерника [14].

Пусть теперь А - выпуклая фигура, а В - единичный круг. Тогда имеет место такая интересная формула (доказанная Штейнером):

В (2) р (А) - периметр (длина границы) А. Для выпуклого многоугольника формула (2) очевидна (см. рис. 61). В общем случае ее можно доказать предельным переходом.

Покажем, как из формул (1) и (2) сразу следует решение классической изопериметрической задачи. Далее мы пользуемся тем, что p(αА) = αр (А) и S (αA) = α²S (A). Имеем

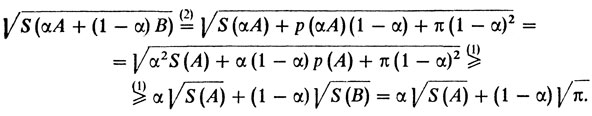
Возводя в квадрат и сокращая одинаковые члены, приходим к изопериметрическому неравенству р² (А) ≥ 4πS (А), которое было получено в итоге второго рассказа. При этом равенство достигается, лишь если А - круг. Вот и еще одно решение задачи Дидоны.

Вернемся снова в XVIII век.

Мы как-то сказали, что Лагранж выдвинул, активно применял и пропагандировал свой принцип снятия ограничений для вариационных задач, но не доказал его. Обоснование этого принципа Лагранжа для задач классического вариационного исчисления стало уделом математиков более поздних поколений, оно было дано в конце XIX века (Майер и др.). И вместе с тем, теорема Лагранжа прямо следует из основных теорем бесконечномерного анализа.

Как же вкладывается классическое вариационное исчисление в бесконечномерный анализ? Приведем один частный, но исключительный по важности случай общей задачи Лагранжа.

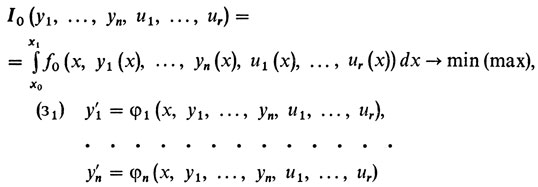
при граничных условиях y_i (х₀) = y_i0, y_i(х₁) = y_i1; i = 1, ..., n.

В этой постановке неизвестные функции разделены на два класса. Одни (y₁(х), ..., y_n(х)) связаны дифференциальными уравнениями. Другие (u₁(х),..., u_n (х)) можно выбирать свободно. Их называют управлениями. Схема дифференциального уравнения или системы таких уравнений с управляющими функциями описывает множество явлений, где допустимо вмешательство человека.

Если считать (при условии, что f₀, φ₁ ,..., φ_n непрерывно дифференцируемы) все игреки непрерывно дифференцируемыми, а управления u₁(х), ..., u_n(х) непрерывными, можно рассмотреть то отображение, которое сопоставляет набору функций y₁(x), ..., y_n(х), u₁(х),..., u_n(х) набор непрерывных функций

Запишем его как(z(х) = (z₁ (х), ...,z_n(х))z(х) = F(y₁ (х),..., u_r(х)). При этом само дифференциальное уравнение в (з х) может рассматриваться как равенство F (y₁ (х), ..., u_r(х)) = 0. В итоге получается задача вида

с краевыми условиями y_i(x₀)= y_i0, y_i(x₁) = y_i1, i = 1,..., n.

И к этой задаче оказывается возможным применить мысль Лагранжа. Функция Лагранжа здесь принимает вид

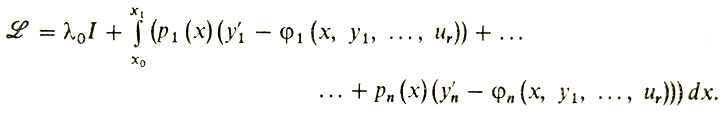
Далее следует мысленно рассмотреть задачу

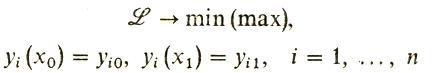
и поступать с нею так, как будто ограничений нет, т. е. писать систему уравнений Эйлера. А справедливость принципа Лагранжа в этом случае выводится из теоремы Люстерника, о которой упоминалось выше.

В заключение расскажем о задачах оптимального управления. Этот важнейший раздел теории экстремальных задач был вызван к жизни задачами технического содержания. Вспомним простейшую задачу оптимального управления из первого рассказа. Пусть имеется тележка, движущаяся прямолинейно без трения по горизонтальным рельсам (см. рис. 62). Тележка управляется внешней силой, которую можно изменять в заданных пределах. Требуется остановить тележку в определенном положении в заданное время. Эту задачу мы называем далее простейшей задачей о быстродействии. Формализуем ее.

Рис. 62

Пусть масса тележки m, ее начальная координата х₀, а начальная скорость υ₀. Внешнюю систему (силу тяги) обозначим через и, а текущую координату тележки - через x(t). Тогда скорость тележки υ (t) = dx (t)/dt, а ускорение a(t) = d²x(t)/dt². Конечный момент времени обозначим через Т. По закону Ньютона m⋅a(t) есть внешняя сила, которая равна u (t). Ограничение на внешнюю силу зададим в виде неравенств u₁ ≤ u (t) ≤ u₂. В итоге получается такая формализация:

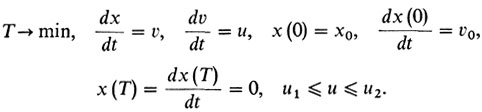
Если бы не было ограничения типа неравенств, эта задача относилась бы к классическому вариационному исчислению. Но наличие ограничения типа нестрогих неравенств на управления не позволяет применять разработанные в вариационном исчислении методы.

Задачи с такими ограничениями получили название задач оптимального управления. Их теория была разработана советским ученым Понтрягиным и его учениками Болтянским, Гамкрелидзе, Мищенко.

Основной метод решения таких задач был открыт в их работах. Он получил название принципа максимума Понтрягина.

Что это такое? Сама задача оптимального управления формулируется почти так же, как (з₁), только на управления налагаются еще дополнительные ограничения, которые мы запишем так:

(*)

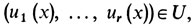где U - это какое-то фиксированное множество векторов (u₁, ..., u_r).

Вот самый простой пример задачи оптимального управления. Пусть f (х, u) - непрерывная функция двух переменных. Рассмотрим задачу

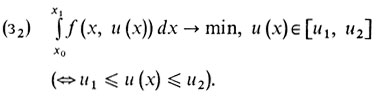
Ограничимся частным случаем такой задачи:

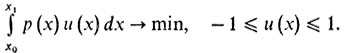
Здесь р (х) - некоторая непрерывная функция на отрезке [x₀, x₁]

Как нам поступить? Совсем нетрудно понять, что наш интеграл будет самым маленьким, если в случае р(х) > 0 мы положим û (х) = -1, а в случае р(х) < 0 положим u (х) равным + 1, т. е. u (х) = -sign р (х). И в общей задаче (з₂) следует поступить аналогичным образом, а именно надо для каждого х из [х₀, x₁] найти то и из отрезка [u₁, u₂], при котором функция f(х, u) (по u) имеет на этом отрезке минимум.

Это можно сформулировать в виде следующего принципа минимума: для того чтобы функция û(⋅) была решением задачи (з₂), необходимо, чтобы

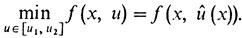
А теперь можно объяснить, в чем состоит принцип максимума. К задаче оптимального управления также применим общий замысел Лагранжа, только его надо чуть модифицировать. Если нам нужно решить задачу оптимального управления (з₂) с дополнительным ограничением (*), то нужно составить функцию Лагранжа L (не отразив в ней ограничение (*)), затем опять-таки мысленно рассмотреть задачу

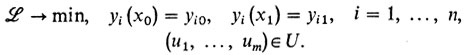
При этом по у надо поступить, как и раньше, т. е. составить уравнения Эйлера, а по и применить принцип минимума. Но так как все члены с и в функцию Лагранжа вошли со знаком "-", удобнее записать его в виде принципа максимума, где (ŷ₁(x), ..., ŷ_n(x), û₁(x), ..., û_r(х)) - решение задачи

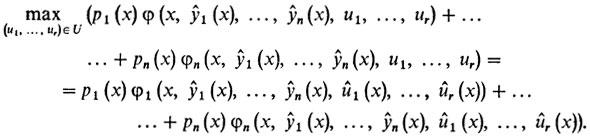
Вот, наконец, и пришло время решить задачу Ньютона.

1° Формализуем задачу Ньютона как задачу оптимального управления:

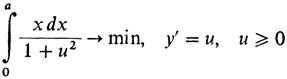
с граничными условиями y (0) = 0, y (а) = b.

2° Применяем принцип Лагранжа. Функция Лагранжа:

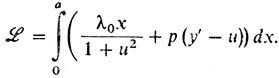
Необходимое условие по y - уравнение Эйлера:

Необходимое условие по u - условие минимальности:

(**)

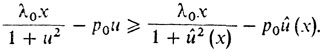3° Если допустить, что λ₀ = 0, то необходимо, чтобы р₀ ≠ 0 (иначе все множители Лагранжа оказались бы нулями). Если же λ₀ = 0 и р₀ ≠ 0, то из (**) следует, что û ≡ 0, а значит, y(х) = ∫^x₀ û(α) dα ≡ 0. Тогда искомое тело "не имеет длины" - оно является плоской пластиной. Если же b > 0, то необходимо считать, что λ₀ ≠ , и тогда можно положить λ₀ = 1. Отметим еще, что случай р₀ ≥ 0 также невозможен, ибо при этом функция (х/(1 + u²)) - р₀u монотонно убывает и (**) невозможно.

Исследуя поведение функции (х/(1 + u²)) - р₀u = φ (u, х) по u, нетрудно убедиться в том, что при р₀ < 0 и малых х функция φ (u, х) достигает минимума при u = 0. Затем оптимальное управление должно быть найдено из уравнения -р₀ = 2ux/(1 + u²)², получающегося из дифференцирования φ(u, х) по и. Момент излома ξ определяется тем, что функция φ(u, ξ) имеет два минимума.

Иначе говоря, в момент излома должны удовлетворяться соотношения (далее через û(ξ) обозначается û (ξ + 0) ≠ 0):

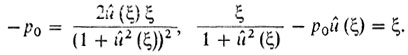
Из второго уравнения получаем -ξû²(ξ)/(1 + û²(ξ)) = р₀û (ξ), откуда р₀ = -ξû(ξ)/(1 + û²(ξ)). Подставив это соотношение в первое из только что написанных уравнений, находим, что û² (ξ) = 1 → û(ξ) = 1, ибо û ≥ 0. И тогда снова из того же уравнения находим, что ξ = - 2р₀.

После излома оптимальное уравнение удовлетворяет соотношению

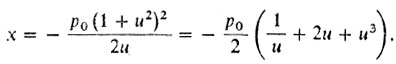
Но

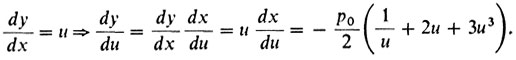
Интегрируя это соотношение с учетом равенства ŷ (ξ) = 0 при û (ξ) = 1 получаем параметрические уравнения кривой Ньютона

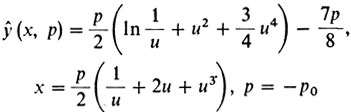
Мы могли бы исследовать и простейшую задачу о быстродействии, но не будем делать этого. Отошлем читателя к книге [1]. где эта задача решена с помощью принципа Лагранжа.

На этом поставим точку. Я выполнил свои обещания и все задачи первой части решил дважды. Давайте отдохнем от формул и поговорим просто так.

Итак, что же сказал бы я "первому встречному школьнику" о теории экстремальных задач (вспомним один из эпиграфов к этому рассказу)? Наверное, что-то в таком роде: в школе тебя учили функциям одного переменного. Там рассказывалось о приеме Ферма решения задач на экстремум таких функций. Но на самом деле имеется множество задач, сводящихся к минимизации функций многих переменных и даже функций от функции (например, от линии), так было, скажем, в задаче о брахистохроне. Их стали исследовать в специальном разделе - вариационном исчислении. В начале нашего века была разработана научная дисциплина - функциональный (бесконечномерный) анализ, в котором обобщается основное понятие "школьного" анализа - понятие производной. Бесконечномерный анализ позволяет с единой точки зрения посмотреть на задачу минимизации функций одного и нескольких переменных и задачи вариационного исчисления.

При этом, если рассматривается задача без ограничений, то теорема Ферма полностью сохраняется: в точке экстремума эта производная должна равняться нулю. Для задач вариационного исчисления теорема Ферма расшифровывается в виде дифференциального уравнения, названного уравнением Эйлера.

Но задач без ограничений сравнительно мало. И среди задач с ограничениями большую долю составляют такие, что их можно формализовать в виде равенств.

Для конечномерных задач с равенствами Лагранж выдвинул принцип их решения. Суть его состоит в том, что надо

составить функцию Лагранжа (т. е. просуммировать минимизируемую функцию и функции, задающие равенства с неопределенными множителями) и затем поступать с ней так, как будто ограничений нет. (Здесь я, может быть, просто процитировал бы слова Лагранжа, поставленные в качестве эпиграфа к двенадцатому рассказу.) Общий замысел Лагранжа сохраняется и для задач вариационного исчисления, и для задач оптимального управления - новой главы теории экстремальных задач.

А если бы мой новый знакомый проявил бы интерес к дальнейшему, я бы рассказал ему то, что написано во второй части этой книги. А следующий рассказ - о некоторых общих вопросах.