Рассказ тринадцатый. Снова порешаем!

Именно здесь мы намереваемся выполнить обещание, которое (возможно, неосторожно) взяли на себя ранее. Наша цель - перерешать все задачи из первой части, и при этом "единообразно, стандартно, если хотите - рутинно", применяя один и тот же (и притом простой) прием, а именно принцип Лагранжа или - в частном случае - теорему Ферма. (В трех случаях нам это сделать все-таки не удастся: мы не сможем справиться с классической изопериметрической задачей, с брахистохроной и задачей Ньютона. Чтобы стандартно Решить их, надо будет еще потрудиться.)

При нашем стандартном исследовании выделяются четыре этапа: 1) формализация; 2) применение принципа Лагранжа или теоремы Ферма; 3) решение соответствующих уравнений и нахождение критических или стационарных точек; 4) отбор нужных точек и обсуждение ответа.

Начнем с задач, сводящихся к нахождению экстремумов функций одного переменного.

1. Задача Евклида о параллелограмме наибольшей площади, вписанном в треугольник (рассказ четвертый).

1° Формализация. Снова обратимся к рис. 12. Пусть, как и раньше, H - высота треугольника ABC, b - длина АС. Обозначим длину AF' через х. Тогда 0 ≤ х ≤ b. Через h = h (х) обозначим высоту треугольника BD'E'. Из подобия треугольников BD'E' и ABC(D'E'║ АС) получаем h(x)/H = x/b. Площадь параллелограмма AD'E'F' равна (Я - h (х)) х = Н (Ь - х) х/Ь. В итоге приходим к следующей формализации:

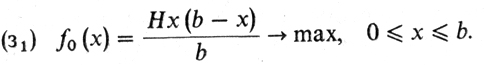
2° Необходимое условие: f'₀(x) = 0.

3° Нахождение критических точек. Стационарные точки: f₀ (х) = (H (bх - х²)/b)' = (b - 2х) Н/b, т. е. f₀ (х) = О лишь в точке b/2. Критические точки: 0, b/2, b.

4° Функция f₀ непрерывна, дифференцируема всюду и рассматривается на конечном отрезке. Значит, решение находится среди критических точек. Перебор критических точек: f₀ (0) = f₀(b) = 0, f₀(b/2) > 0.

Таким образом, решение (з₁) есть b/2. Ответ:искомый параллелограмм ADEF характеризуется тем, что точка F является серединой отрезка [А С]. Именно этот факт и был установлен Евклидом.

2. Задача Архимеда о шаровом сегменте наибольшего объема среди изопифанных (рассказ четвертый).

1° Формализация. Пусть R - радиус шара, a h - высота шарового сегмента. Объем шарового сегмента, как известно, равен πh² (R - h/3), а площадь его боковой поверхности - 2πRh. Площадь боковой "поверхности задана: 2πRh = а, откуда R = a/2πh. Подставляя это выражение вместо R в формулу для объема и учитывая, что h ≤ 2R = а/πh, получаем следующую формализацию:

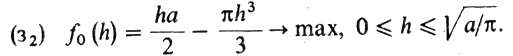
2° Необходимое условие: f'₀ (h) = 0.

3° Нахождение критических точек. Стационарные точки: f₀ (h) = (ha/2 - πh³/3)' = а/2 - πh², т. е. f₀(h)' = 0

лишь в случае, когда h = √а/2π. Критические точки: 0, √а/2π, √а/π.

4° Функция f₀ непрерывна, дифференцируема всюду и рассматривается на конечном отрезке. Значит, решение находится среди критических точек.

Перебор критических точек: f₀(0) = 0, f₀(√а/2π) = √2 а^3/2/6√π, f₀ (√a/π) = а^3/2/6√π. Максимальное значение доставляет точка √а/2π. Это и есть решение. Вспомнив, что a = 2πRh, получаем h = R. Ответ:искомый шаровой сегмент является полушаром - высота равна радиусу. Именно этот результат и был доказан Архимедом.

3. Задача о наименьшей площади (рассказ четвертый).

1° Формализация. Снова обратимся к рис. 17. Проведем через точку М прямую, параллельную АВ, и точку пересечения этой прямой с АС обозначим через N. Пусть Е - некоторая точка на луче NC, а = |AN|, х = |NE'|, D' - точка пересечения луча АВ и прямой Е'М. Треугольники ME'N и AD'E' подобны, ибо MN ║ АВ. Значит, их площади относятся как квадраты длин отрезков [NE'] и [АЕ']. Но площадь треугольника ME'N равна xh/2, где h - высота, опущенная из М на АС. Отсюда получаем, что площадь треугольника AD'E' равна h (х + а)²/2х, и мы приходим к такой формализации :

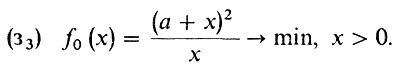
2° Необходимое условие: f₀(х) = 0.

3° Нахождение стационарных точек:

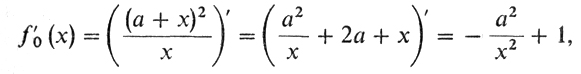
т. е. f'₀(x) = 0 лишь в случае х = а.

4° Функция f₀ удовлетворяет требованиям следствия из теоремы Вейерштрасса из рассказа одиннадцатого. Значит, решение задачи (з₃) существует. В силу дифференцируемости f₀ для x > 0 и теоремы Ферма решение должно быть стационарной точкой. Но стационарная точка единственна. Значит, она и является решением. Ответ:искомая точка Е удалена от А на расстояние 2а. Отсюда сразу следует, что точка M делит отрезок DE пополам (из подобия треугольников ENM и EAD). Именно этот результат и был получен нами ранее геометрическим путем.

4. Задача Герона. Она уже много раз встречалась у нас - в первом, втором, десятом и одиннадцатом рассказах. Пришло время решить ее стандартно.

1° Формализация уже была проведена в рассказе десятом:

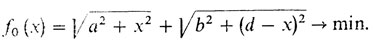
2° Необходимое условие: f'₀ (х) = 0.

3° Нахождение стационарных точек. Применяя теорему о дифференцировании сложной функции, получим: (√(а² + х²)' = х/√(а² + х²) (это было подробно проделано в одиннадцатом рассказе);

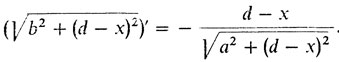
Отсюда получаем

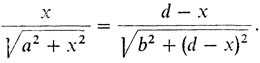
Решим полученное уравнение. Возводя в квадрат, "переворачивая" и вычитая по единице, приходим к соотношению (а/х)² = (b/(d - х))², откуда (отбросив посторонний корень) получаем, что х/а = (d - x)/b (это согласуется с тем, что говорилось в первом рассказе - см. рис. 1). Решение полученного уравнения обозначим через х̂.

4° Функция f₀ (х) как сумма двух выпуклых функций выпукла, кроме того, она гладкая. Значит, как было сказано в конце предыдущего рассказа, х̂ - решение задачи, причем единственное в силу строгой выпуклости f₀ (х).

Взглянем еще раз на самый первый рисунок этой книги. Величина х̂/√(а² + х²) равна sin φ₁ величина d - х̂/√(b² + (d - х)²) равна sin φ₂. Из (1) следует, что sin ₁ = sin φ₂, т. е. φ₁ = φ₂.

Ответ:решение задачи Герона характеризуется тем, что угол падения равен углу отражения. Этот факт и был доказан нами на первых же страницах этой книги.

В первом рассказе были сформулированы две задачи - № 1 и 2, примыкающие к задаче Герона. Но они тривиально к ней сводятся. Докажите, что в задаче 1 решение существует. Тогда, если оно не совпадает с вершиной угла, оно является решением задачи Герона для В и С и той стороны угла, где должна находиться точка А. Значит, у точки А угол падения равен углу отражения. Аналогичное утверждение верно и для точки В. Это приводит к нужному построению. Так же решается и задача 2, поэтому нет нужды решать их формально.

5. Задача Снеллиуса о законе преломления (рассказ третий). Пришло время и эту задачу решить стандартно - так, как это впервые сделал Лейбниц.

1° Формализация. Направим ось Ох по прямой, разделяющей две среды, а ось Оy проведем перпендикулярно оси Ох через точку А (см. рис. 9). Пусть координаты точек А, В оказались такими: А = (0, а), В = (d, - b). Возьмем на оси точку D' с координатой (х, 0). Тогда время, затрачиваемое светом на преодоление пути AD'B, равно √(а² + х²)/υ₁ + √(b² + (d - x)²)/υ₂.

В итоге получается задача без ограничений:

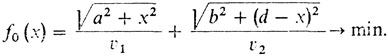
2° Необходимое условие: f'₀ (х) = 0.

3° Нахождение стационарных точек:

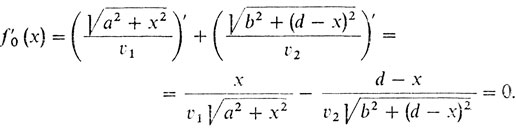(1)

(По поводу дифференцирования см. предыдущую задачу.) Вследствие монотонности функций x/υ₁√(a² + х²) и (d -x)/υ₂√(b² + (d - х)²) получаем, что имеется единственное решение х уравнения f'₀ (х) = 0.

4° Функция f₀ (х) выпукла, значит, теорема Ферма является достаточным условием экстремума, т. е. х̂ - решение. Из строгой выпуклости f₀ (х) следует, что это решение единственно. Из рис. 9 и соотношения (1) получаем равенство

выражающее закон Снеллиуса. Ответ: решение в задаче Снеллиуса характеризуется тем, что отношение синусов угла падения и угла преломления равно отношению скоростей в первой и второй средах. Этот факт был установлен нами в третьем рассказе.

6. Планиметрическая задача Кеплера о прямоугольнике максимальной площади, вписанном в круг. Об этой задаче говорилось в рассказах пятом и десятом; формализована она была в десятом рассказе.

1° Формализация.

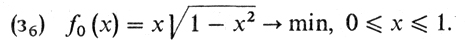
2° Необходимое условие: f₀(х) = 0.

3° Нахождение критических точек. Стационарные точки: f'₀ (х) = 0.

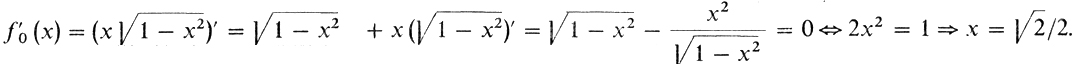
Таким образом, имеются 3 критические точки: 0, 1, √2/2.

4° Функция f₀ непрерывна на [0, 1] и дифференцируема в интервале (0, 1). Значит, решение находится среди критических точек. Перебор критических точек: f₀ (0) = f₀ (1) =0, f₀ (√2/2) = √2/4. Таким образом, решение (з₆) есть √2/2. В этом случае, как это следует го формализации, прямоугольник является квадратом. Ответ: максимальный из вписанных в круг прямоугольников - квадрат.

7. Задача Кеплера о вписанном цилиндре. Об этой задаче речь шла в шестом рассказе.

1° Формализация. Пусть шар имеет радиус R. Обозначим половину высоты цилиндра через х. При этом 0 ≤ х ≤ R. Тогда радиус основания цилиндра равен √(R² - х²) и его объем равен πr²x = 2π(R², - х²) х. Таким образом, приходим к формализации:

(Фактически эта задача была формализована уже в шестом рассказе.)

2° Необходимое условие: f₀ (х) = 0,

3° Нахождение критических точек. Стационарные точки:

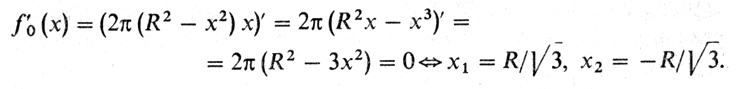
Второй корень не подходит (x₂ < 0). Таким образом, имеются

3 критические точки: 0, R/√3 и R.

4° Функция f₀ непрерывна и дифференцируема всюду. Значит, решение находится среди критических точек. Вследствие того, что f₀(0) = f₀(R) = 0, получаем, что решение равно R/√3, отсюда следует, что радиус минимального цилиндра равен

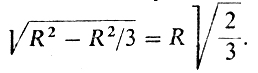
Ответ: Отношение высоты экстремального цилиндра к диаметру основания равен √2. Именно этот факт и был установлен Кеплером.

Перейдем теперь к решению некоторых алгебраических задач.

8. Задача Тартальи (рассказ пятый).

1° Формализация. Обозначим через х меньшее из чисел. Тогда 0 ≤ x ≤ 4 и 8 - х - большее число. Их разность равна 8 - 2х. В итоге

2° Необходимое условие: f₀ (х) = 0.

3° Нахождение критических точек. Стационарные точки:

Второй корень не подходит (х₂ > 4). Таким образом, имеются три критические точки: 0, 4 и 4 - 4/√3.

4° Функция f₀ непрерывна и дифференцируема всюду и рассматривается на конечном отрезке. Значит, решение находится среди критических точек. Но f₀ (0) = f₀ (4) = 0, f₀(4 - 4/√3) > 0. Значит, решение (з₈) есть 4 - 4/√3.

Ответ: большее число равно 4 + 4/√3, меньшее равно 4 - 4/√3. Именно этот факт и был установлен Тартальей.

9. Неравенство между средним геометрическим и средним арифметическим (рассказ пятый).

Рассмотрим вспомогательную экстремальную задачу:

Функции f_i непрерывны и их частные производные непрерывны. Совокупность допустимых точек ограничена, ибо 0 ≤ x_k ≤ 1 для любого к. Значит, по теореме Вейерштрасса решение х̂ = (х̂₁ ,..., х̂_n) существует. При этом, конечно, x̂_k ≠ 0, ибо иначе f₀ (х̂) = 0, в то время как существуют допустимые элементы, для которых f₀ (х) > 0.

Решение х̂ будет, конечно, и локальным минимумом в задаче (з₉), откуда (вследствие того, что по доказанному х̂_k > 0) оно будет локальным минимумом и в задаче без неравенств.

1° Формализация:

Функция Лагранжа для (з')L (х, λ₀, λ₁) = λ₀f₀(х) + λ₁f₁(х).

2° Необходимое условие - правило множителей Лагранжа:

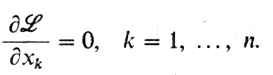
3° Нахождение стационарных точек. Обозначим произведение x̂₁,...х̂_n, через А. Тогда

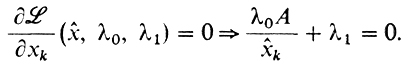
Если допустить, что λ₁ = 0, то сразу приходим в противоречие с тем, что оба множителя, λ₀ и λ₁ не могут быть нулями. Тогда получаем x̂_i = -λ₀A/λ₁ т. е. х̂₁ = ... = х̂_n = 1/n (из-за того, что x̂₁ + ... + х̂_n = 1).

4° Вследствие того, что стационарная точка в (з') единственна, она и доставляет решение задачи.

Теперь докажем нужное неравенство. Пусть a₁,..., а_n - любые неотрицательные числа. Положим S = a₁ + ... + а_n и x_j = A_I/S. Тогда х₁ + ... + х_N = 1, и значит, по доказанному

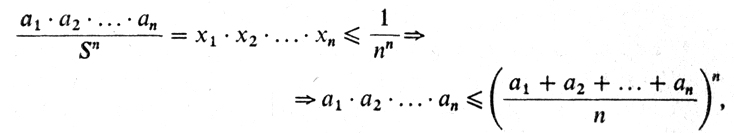
что и требовалось доказать.

10. Неравенства между средним арифметическим и средним квадратическим (рассказ пятый).

Снова рассмотрим вспомогательную задачу.

1° Формализация:

Функции f₀ и f₁ и их частные производные непрерывны. Совокупность допустимых точек ограничена, ибо - 1 ≤ x_k ≤ 1, k = 1,...., n. Значит, решение х̂ = (х̂₁ ,..., х̂_n) существует и можно применять принцип Лагранжа. Функция Лагранжа L(х, λ₀, λ₁) = λ₀f₀(х) + λ₁f₁(х).

2° Необходимое условие:

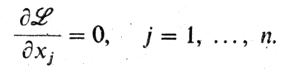
3° Нахождение стационарных точек:

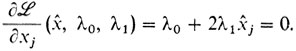
Если допустить, что λ₁ = 0, то сразу приходим в противоречие с тем, что оба множителя Лагранжа не могут быть нулями. Тогда получаем, что х̂_j = -λ₀/2λ₁, т. е. х̂₁ = ... = х̂_n = 1/√n (из-за того что х̂²₁ + ... + х̂²_n = 1).

4° Вследствие того, что стационарная точка единственна, она и доставляет решение задачи.

Теперь докажем нужное неравенство. Пусть а , ..., а_n - любые числа. Положим S - (а²₁ + ... + а²_n)^1/2 и x_j = a_j/S. Тогда х²₁ + ... + х²_n = 1, и значит, по доказанному

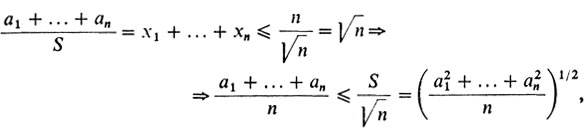
что и требовалось.

Заодно мы доказали и неравенство (для неотрицательных д,)

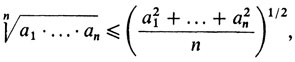
решив тем самым планиметрическую и одну из стереометрических задач Кеплера, о которых шла речь в пятом рассказе.

Отметим еще, что, действуя совершенно аналогично, можно было бы доказать следующие общие неравенства для средних. Пусть а₁, ..., а_n - неотрицательные числа. Положим S_p = ((a^p₁ +...+ a^p_n)/n)^1/p, ∑_p = (a^p₁ + .... + a^p_n). Тогда

Выше мы доказали частный случай (1), когда р = 1, q = 2.

11. Неравенства Коши - Буняковского и Гельдера (рассказ пятый). Пусть а₁, ..., а_n - фиксированные числа, не равные одновременно нулю.

1° Рассмотрим экстремальную задачу:

Функции f₀ и f₁ и их частные производные непрерывны. Совокупность допустимых точек ограничена, ибо - В ≤ x_j ≤В, j = 1,..., n. Значит, решение х̂ = (х̂₁ ,..., х̂_n) существует и можно применять принцип Лагранжа. Функция Лагранжа L (х, λ₀, λ₁) = λ₀f₀(х) + λ₁f₁(х). Положим A = (a²₁ + ... + а²_n)^1/2.

2° Необходимое условие:

3° Нахождение стационарных точек:

Если допустить, что ₁ = 0, то сразу приходим к противоречию с тем, что оба множителя Лагранжа не могут быть нулями. Тогда мы получаем

откуда вследствие равенства х̂²₁ + ... + x̂²_n = В² получаем, что

4° Имеются лишь две стационарные точки. Решением является та точка, где взят знак плюс: х̂_j = Ba_j/A.

Пусть теперь b₁, ..., b_n - также любой набор чисел и В² = b²₁ + ... + b²_n. Тогда по доказанному

Но это и есть неравенство Коши - Буняковского.

Неравенство Гельдера доказывается точно так же. Укажем без комментариев необходимые выкладки.

1° Формализация:

Функция Лагранжа: L = λ₀f₀(х) + λ₁f₁(х). А^def =(а^p'₁ + ... + а^p'_n), р^'-1 + р^-1 = 1.

2° Необходимое условие:

3° Нахождение стационарных точек:

λ₀a_j + pλ₁|x_j|^p-1sing x_j = 0 → x̂_j = Ca^p'-1_j, C = ±B/A^p'/p

4° Решение: x̂_j = Ba^p'-1_j/A^p'/p, j = 1, ..., n.

Пусть теперь b₁,...., b_n - любой набор неотрицательных чисел. Тогда по доказанному

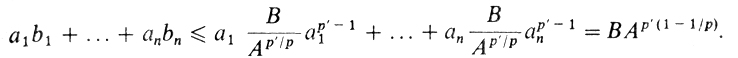
Но это и есть неравенство Гельдера.

И снова вернемся к геометрии.

12. Задача Штейнера (рассказ четвертый). Пусть координаты трех заданных точек таковы: А = (а₁, а₂), В = (b₁, b₂), С = (с₁, с₂). Координату точки D обозначим через (х₁, х₂). Тогда сумма расстояний от D до А, В и С равна

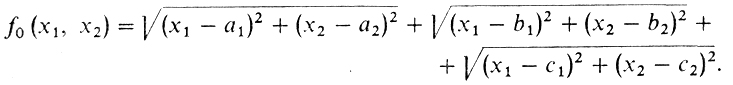
Это приводит к задаче без ограничений.

1° Формализация:

Заметим, что если х²₁ + х²₂ велико, это означает, что точка D расположена далеко от точек А, В и С, и значит, сумма расстояний от нее до этих точек также велика. Следовательно, f₀ (х) → ∞, когда х²₁ + х²₂ → ∞, поэтому можно применить следствие из теоремы Вейерштрасса из предыдущего рассказа. Согласно этому следствию решение х̂ = (х̂₁, х̂₂) задачи (з₁₂) существует.

Легко понять, что во всех точках х, кроме точек А, В и С, частные производные функции f₀ существуют и непрерывны.

2° Необходимое (и в силу выпуклости f₀ - достаточное) условие - теорема Ферма. Если x̂ ≠ А, В или С, то

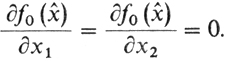
3° Нахождение стационарных точек:

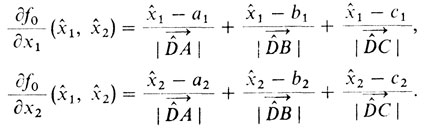
4° Раскроем геометрический смысл написанных соотношений. Они означают, что три вектора единичной длины

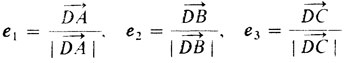
в сумме равны нулю. Но тогда из них можно составить равносторонний треугольник, т. е. величины углов AD̂B, BD̂C и CD̂A равны 120°. Значит, если решение не совпадает с одной из вершин треугольника AВС, то D̂ - это такая точка, из которой все стороны видны под углом 120°. Это не что иное, как точка Торричелли, о которой говорилось в четвертом рассказе (там же мы учились ее строить). Если тупой угол в треугольнике ≥ 120°, то нет такой точки, из которой все стороны видны под углом 120°.

Значит, точка х̂ обязана совпадать с одной из вершин, а именно с вершиной тупого угла, ибо против большего угла лежит большая сторона. (Пусть тупой угол - при вершине С. Тогда - при естественных обозначениях сторон с > а и с > b, откуда следует, что a + b < a + c и a + b < b + с, т. е. минимальная сумма - это а + b.)

Ответ. Если все углы треугольника < 120°, то искомая точка есть точка Торричелли, если один из углов ≥ 120°, то искомая точка расположена в вершине этого угла.

Именно к такому ответу мы пришли в четвертом рассказе.

В первом рассказе была сформулирована задача 4, непосредственно примыкающая к задаче Штейнера. Ответ к ней бььт приведен в четвертом рассказе. В части, касающейся выпуклого четырехугольника, ответ немедленно следует из достаточности теоремы Ферма для выпуклой задачи без ограничений. В невыпуклом случае, так же, как и в задаче Штейнера, доказывается, что решение существует, и после этого остается проверить, что если точка отлична от вершины, то необходимое условие не может быть выполнено.

13. Задача о наименьшем периметре (четвертый рассказ).

Обратимся к рис. 18. Проведем через точку М прямые, параллельные АВ и АС, и точки пересечения с АС и АВ соответственно обозначим через N и Р. Обозначим |AN| = a, |АР| через b, угол ВАС через α, отрезок, проходящий через точку М, через [DE] (D лежит на АВ, Е - на AC), |NE| через х, |PD| через y, углы ADE и DEC соответственно через χ и φ.

Из подобия треугольников PDM и NME получаем х/b = а/y → хy = ab. По теореме косинусов

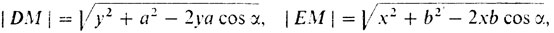
откуда периметр треугольника AD'E' оказывается равным

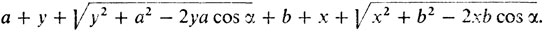
1° В итоге приходим к такой формализации:

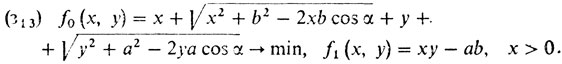
Выразив y через х и подставив в минимизируемую функцию, приходим к задаче

где f₀ (х) → ∞ при х → 0 и f₀ (х) → ∞ при х → ∞ (проверьте).

Значит, по следствию из теоремы Вейерштрасса из одиннадцатого рассказа решение задачи (з'₁₃), а следовательно, и решение задачи (з₁₃) существуют. Обозначим его (х̂, ŷ). Применяем принцип Лагранжа. Функция Лагранжа L(х, y, λ₀, λ₁) = λ₀f₀(x, y) + λ₁f₁(х, y).

2° Необходимое условие:

Нахождение стационарных точек:

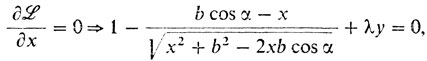
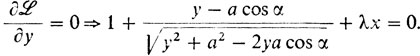
4° Раскроем геометрический смысл написанных соотношений. Для этого опустим перпендикуляры MR и MS на АС и АВ соответственно. Тогда, как видно из рис. 18,

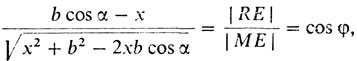
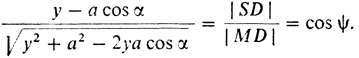
Соотношения п. 3° можно преобразовать, умножив первое на х, второе на y и использовав написанные равенства и равенство хy = ab:

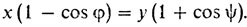
Теперь из треугольников MNE и DPM получаем по теореме 5 синусов:

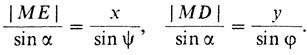
Откуда окончательно

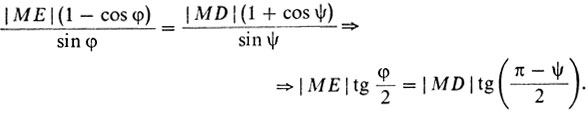
Это последнее соотношение имеет следующий геометрический смысл: перпендикуляр к отрезку DE в точке М пересекается с биссектрисами внешних углов D и Е в одной точке О. Иначе говоря, вневписанная по отношению к треугольнику ADE окружность проходит через точку М.

Именно этот ответ и был получен в четвертом рассказе.

14. Задача Аполлония.

В четвертом рассказе говорилось, что геометрические задачи на экстремум встречаются у всех трех величайших математиков античности - Евклида, Архимеда и Аполлония. Но затем были приведены лишь задачи Евклида и Архимеда.

Задачу Аполлония мы не решились привести. И вот почему.

"Коника", или "Конические сечения", - так называется величайшее творение Аполлония (III-II века до н. э.). Принято считать, что "Коника" - это вершина античной математики. К нашей теме относится пятая книга "Конических сечений". Она не переведена на русский язык, и мы приведем цитату из книги "Пробуждающаяся наука" (М.: Гостехиздат, 1954), принадлежащей перу Ван дер Вардена, известного математика и историка нашей науки. Ван дер Варден пишет так: Аполлоний ставит "задачу о том, как провести из одной точки О к коническому сечению самый длинный и самый короткий прямолинейные отрезки. Однако он дает больше, чем обещает: он определяет все проходящие через О прямые, которые пересекают коническое сечение под прямым углом (в настоящее время их называют нормалями), разбирает, при каком положении О задача имеет два, три или четыре решения". Перемещая точку О, он "определяет ординаты граничных точек G₁ и G₂, где число проходящих через О нормалей разом переходит с 2 на 4 и обратно" (рис. 49).

Я не формулировал задачу Аполлония в четвертом рассказе, во-первых, потому, что понятие "коническое сечение" не проходят в школе, а во-вторых, потому, что совершенно не представляю себе, как можно решить задачу, о которой говорит Ван дер Варден, оставаясь в рамках старой элементарной математики. А без такого решения мне не хотелось затрагивать эту задачу в первой части.

В седьмом рассказе, когда речь шла о брахистохроне, отмечалось, что в античные времена рассматривали лишь прямые, окружности и конические сечения (которые, собственно, и исследовал Аполлоний). Но кривая, разделяющая области, где число нормалей равно двум и четырем (она называется астроидой) принадлежит к совсем другому типу кривых. Она появилась лишь в XVII веке. Трудно даже вообразить, как можно было выразить ее, не прибегая к языку алгебры. (Вспомните эти слова, когда мы найдем уравнение астроиды !)

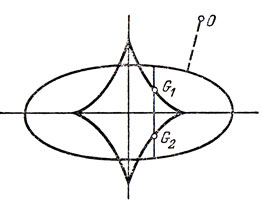
Рис. 49

А теперь перейдем к решению поставленных задач. Сформулируем их так:

1) Как найти расстояние от точки до конического сечения?

2) Сколько нормалей можно провести из точки к коническому сечению?

Мы не будем решать задачи для всех конических сечений, а ограничимся лишь случаем эллипса.

В декартовой системе координат эллипс записывается уравнением (x₁/a₁)² + (х₂/а₂)² = 1. Далее считаем, что a₁ ≥ а₂ > 0, т. е. "ширина" эллипса не меньше его "высоты". Если а₁ = а₂ т. е. если ширина и высота совпадают, то эллипс становится окружностью. Решим первую задачу.

1° Формализация. Пусть точка О имеет координаты (ξ₁,ξ₂)- Расстояние от точки О до точки с координатами (x₁, x₂) равно ((x₁ - ξ₁)² + (х₂ - ξ₂)²)^1/2. Для удобства вместо расстояния будем минимизировать квадрат расстояния. В итоге получаем задачу

Функции f₀ и f₁ и их частные производные непрерывны, совокупность допустимых точек ограничена, ибо -а₁ ≤ x_j ≤ a₁ j = 1, 2. Значит, решение х̂ = (х̂₁, х̂₂) существует и можно применять принцип Лагранжа. Функция Лагранжа

2° Необходимое условие:

3° Нахождение стационарных точек:

Если допустить, что λ₀ = 0, то λ₁ ≠ 0 (ведь множители Лагранжа не могут равняться нулю одновременно). Значит, из написанных уравнений последует, что х̂₁ = х̂₂ = 0, т. е. f₁ (0, 0) = 0 ≠ 1 = f₁ (х̂₁, х̂₂) - противоречие. Итак, λ₀ ≠ 0, и можно положить λ₀ = 1. Обозначим при этом λ₁ = λ. Тогда из полученных уравнений

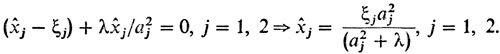
Подставляя эти соотношения в уравнения эллипса, приходим к уравнению

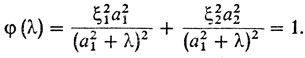
4° Число стационарных точек задачи (т. е. точек, соответствующих тем λ, которые удовлетворяют уравнению φ (λ) = 1) не больше четырех (ибо получилось уравнение четвертой степени, см. также рис. 50. Неравенство φ(0) = ξ²₁/a²₁ + &ξ²₂/а²₂ > 1 на рис. 50 показывает, что функция φ изображена для точки (ξ₁, ξ₂) лежащей вне эллипса).

По-видимому, невозможно записать решение этого уравнения в сколько-нибудь простом явном виде. Но сейчас, когда в нашем распоряжении имеются многочисленные вычислительные средства, мы, конечно, можем получить приближенное решение уравнения φ (λ) = 1 очень скоро и с любой точностью. После того как корни _i уравнения будут вычислены, нужно будет найти соответствующие точки (x₁ (λ_i), х₂ (λ_i)), подставить эти значения в f₀ и найти наименьшее из полученных чисел.

Итак, первая задача решена. Полученные нами соотношения (x̂_j - ξ_j) + λx̂_j/a²_j = 0 имеют такой геометрический смысл: вектор ξ - х̂, соединяющий точку О с минимальной точкой на эллипсе, пропорционален вектору-градиенту функции f₁ в точке х̂, т. е. вектор ξ - х̂ лежит на нормали к эллипсу. Этот факт был впервые установлен Аполлонием.

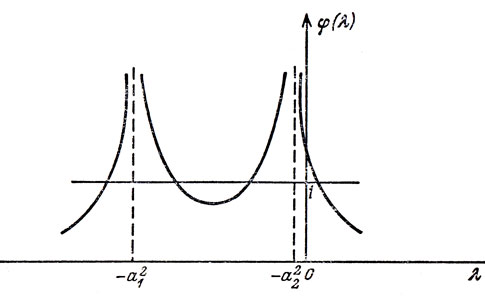
Рис. 50

А теперь примемся за вторую задачу. Выведем уравнения той "разделяющей" кривой, которая отделяет область, где можно провести две нормали, от области, где их можно провести четыре. Из рис. 50 легко понять, что это разделение происходит для тех λ, для которых удовлетворяются условия φ (λ) = 1, φ' (λ) = 0 - ведь именно тогда кривая y = φ (λ) касается прямой y = 1. Значит, надо освободиться от λ из соотношений

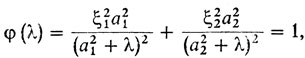
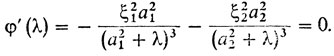
Из последнего уравнения получаем

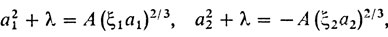
где

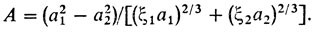
Подставляя эти соотношения в уравнение φ (λ) = 1, приходим к уравнению разделяющей кривой

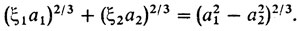
Это и есть уравнение астроиды, о которой было сказано выше (как его мог получить Аполлоний?). Вне астроиды каждая точка имеет две нормали, внутри нее - четыре (в частности, конечно, - в центре эллипса), а на самой астроиде - три (за исключением вершин, где имеются две нормали).

Вот, наконец, мы добрались до того результата, который был получен еще во II веке до н. э.

В 1975 году была организована первая всесоюзная Олимпиада "Студент и научно-технический прогресс". На эту Олимпиаду съехались около ста лучших студентов-математиков всех наших республик. Среди других задач была предложена задача Аполлония: сколько нормалей можно провести из точки к эллипсу? С задачей справился лишь один человек, хотя организаторам, признаться, казалось, что за 22 столетия можно было бы достичь и большего.

Решим еще несколько задач. Летом 1984 года мне предложили провести занятие со школьниками, готовящимися к выступлению на международной математической олимпиаде. Была названа тема занятия - "Математический анализ". Чтобы продемонстрировать силу математического анализа, я решил рассказать то, что уже известно моему читателю из второй части этой книги. Затем на занятии было устроено нечто вроде состязания между анализом и геометрией. Я предлагал задачу, школьники решали ее геометрически, а я - аналитически. Я был убежден в преимуществе анализа и рассчитывал на легкую победу. Однако дело оказалось совсем не таким простым. Мои слушатели были истинными любителями геометрии и, кроме того,-замечательно тренированными в решении задач. Ребятам ничего не стоило придумать неожиданные и очень изящные решения, которые, как мне казалось, совсем нелегко найти. А они считали их тривиальными. Легкой победы не получилось. Но все же нельзя считать, что математический анализ потерпел фиаско. Ниже предлагаются три задачи из этого моего занятия со школьниками, в которых, как мне кажется, "теория" вполне сумела за себя постоять.

Я предлагаю далее лишь аналитические решения. Попробуйте найти "чисто геометрические" решения, которые были бы убедительно проще приведенных!

Первая задача предлагалась на Всесоюзной математической олимпиаде школьников в 1980 году. Ее автор - И. Ф. Шарыгин, известный своим исключительным умением придумывать красивые геометрические задачи (см. [21], задача 349).

15. Дан круг радиуса единица. На диаметре 4В дана точка F, через которую проводится хорда CD. Найти положение хорды, при котором площадь четырехугольника ACBD максимальна.

Решение. 1° Формализация. Пусть О - центр круга, |OF| = а, угол СРВ обозначим через φ (рис. 51). Вспомним, что площадь четырехугольника, вписанного в окружность, равна полупроизведению диагоналей на синус угла между ними.

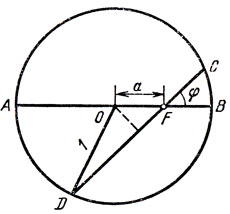
Рис. 51

Ясно, что |CD| = 2√(1 - a² sin² φ). Отсюда приходим к такой формализации:

Делаем замену a sin φ = √z и приходим к задаче

По теореме Вейерштрасса решение существует.

2° Необходимое условие - теорема Ферма: f'(ẑ) = 0.

3° Нахождение критических точек. Стационарная точка одна: ẑ = 1/2 (если а² > 1/2). Критические точки: {0, а²}, если а² ≤ 1/2, и {0, 1/2, а²}, если а² > 1/2.

4° Сравнивая значения f в критических точках, приходим к ответу: если 0 ≤ а ≤1/√2, то ẑ = а², т. е. φ̂ = π/2; если 1/√2 < а ≤ 1, то ẑ = 1/2, т. е. φ̂ = arcsin (1/а√2).

Эту задачу предложили мне сами школьники. Они были убеждены, что их геометрическое решение будет несравненно проще любого аналитического. Но разве может быть что-нибудь проще решения, приведенного нами?

Следующая задача также принадлежит И. Ф. Шарыгину. Он придумал ее специально для занятий с этой группой. (Ее предполагалось использовать в подготовительных конкурсах, но этого не произошло, так что задача оказалась неизвестной моим слушателям. Они, зная И. Ф. Шарыгина, который также занимался с ними, предвкушали очередную легкую победу геометрии.) Вот как она звучит (см. [21], задача 348).

16. Дан угол ВАС и две точки М и N внутри него. Провести (циркулем и линейкой) через точку М отрезок DE так, чтобы площадь четырехугольника ADNE была минимальной (рис. 52).

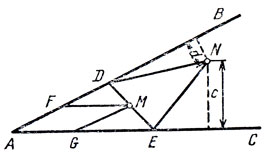
Рис. 52

Решение. 1° Формализация. Проведем отрезки MF и MG параллельно сторонам АС и АВ соответственно и длины этих отрезков обозначим а и b. Опустим из N перпендикуляры на АВ и АС и длины этих перпендикуляров обозначим due. Тогда удвоенная площади ADNE равна (b + x)d + + (а + y) где х = |FD|, y = |GE||. При этом ху = ab, что сразу следует из подобия треугольников DFM и MGE. Таким образом,

Из теоремы Вейерштрасса следует (продумайте!), что решение (х̂, ŷ) задачи существует (ибо f₀ растет на бесконечности). Функции f₀ и f₁ и их производные непрерывны, значит, можно применять принцип Лагранжа. Функция Лагранжа

2° Необходимые условия:

3° Нахождение стационарных точек:

Ясно, что λ₀ ≠ 0 (ибо иначе х̂ = ŷ = 0, т. е. х̂ŷ = 0 ≠ ab), и значит, можно положить λ0Ρ = 1. В итоге приходим к системе уравнений

4° Построение. Строим (циркулем и линейкой) отрезок f из отношения f/b = a/d (вспомните, как это делается, посмотрев на рис. 53) и затем строим (снова циркулем и линейкой - см. рис. 22) х̂ из соотношения х̂² = сf ↔ x̂ = √cf Существуют и чисто геометрические решения, в частности, очень красивое - авторское. Они приводят к другим методам построения. Найдите их и сравните. Найти более простое геометрическое решение моим слушателям не удалось!

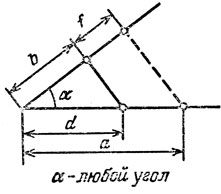
Рис. 53

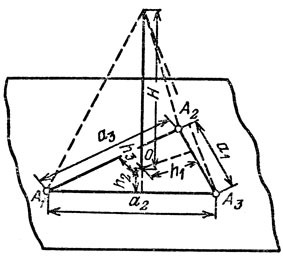
Рис. 54

17. Среди всех пирамид с данными основаниями и высотой найти пирамиду с наименьшей боковой поверхностью.

Решение. 1° Формализация (см. рис. 54). Пусть основание пирамиды - это треугольник A₁A₂A₃ с длинами сторон а₁, а₂ и а₃ (a_j > 0, j = 1, 2, 3), О - проекция вершины на плоскость основания. Высоту пирамиды обозначим через H, а через h₁, h₂, h₃ обозначим расстояния от О до прямых, содержащих стороны А₂А₃, А₁А₃ и А₁А₂ соответственно (взятые со знаком плюс, если О лежит в той же полуплоскости, что и треугольник А₁А₂А₃, и со знаком минус - если в другой). Тогда имеет место известное (и очевидное) равенство a₁h₁ + a₂h₂ + a₃h₃ = 25, где S - площадь основания. При этом боковая поверхность пирамиды равна

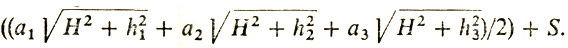
Приходим к задаче

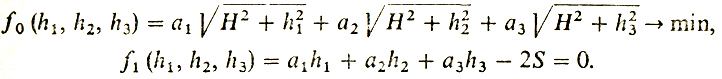
По теореме Вейерштрасса (продумайте!) решение задачи существует (ибо f₀ растет на бесконечности). Функции f₀ и f₁ и их частные производные непрерывны. Значит, решение ĥ = (ĥ₁, ĥ₂, ĥ₃) существует и можно применять принцип Лагранжа. Функция Лагранжа L = λ₀f₀ + λ₁f₁.

2° Необходимые условия: dL/dh_j = 0, (j = 1, 2, 3).

3° Нахождение стационарных точек:

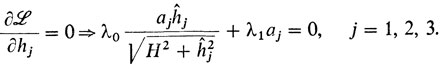
Ясно, что λ₀ ≈ 0, и можно считать, что λ₀ = 1.

4° Сокращая на a_j в полученных уравнениях, немедленно получаем, что ĥ₁ = ĥ₂ = ĥ₃, т. е. проекция высоты - это центр вписанного круга.

... После недолгого размышления один из моих слушателей назвал правильный ответ. Я вызвал его к доске, ожидая в очередной раз выслушать "чисто геометрическое" решение, сопровождаемое ироническими замечаниями. Но неожиданно я увидел выписанными функции f₀ и f₁ функцию Лагранжа, ее частные производные и - ответ.

Да здравствует математический анализ! Не так ли?

С нетерпением ожидал я вестей с 25-й Международной математической олимпиады, которая в 1984 году проходила в Праге. Сначала стало известно, что наша команда выступила с успехом, ребята получили пять первых и одну вторую премию и набрали 225 очков. С таким успехом не выступала ни одна команда за всю историю олимпиад. Потом я получил и задачи. Конечно, больше всего меня интересовало, были ли среди них такие, где можно применять методы исследования экстремальных задач. И там-таки была одна такая задача.

18. Пусть х, y, z - неотрицательные действительные числа такие, что х + y + z = 1. Докажите, что

Решение. 1° Формализация:

По теореме Вейерштрасса решение задачи существует и на максимум, и на минимум. Допустим, что некоторое решение (х̂, ŷ, ẑ) таково, что все эти числа отличны от нуля. Но тогда это же решение будет доставлять локальный экстремум задаче f₀ (х, y, z) → max (min), f₁ (x, y, z) = 0, и к ней можно применять правило множителей Лагранжа.

2° Необходимое условие (для функции, Лагранжа L = λ₀f₀ - λ₁f₁):

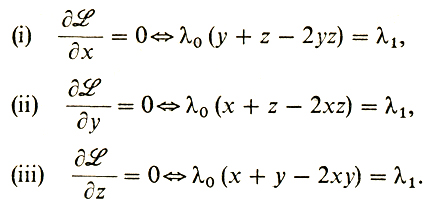
Ясно, что λ₀ не может равняться нулю (иначе λ₁ = 0). Далее λ₀ = 1.

3° Нахождение стационарных точек. Вычитая из уравнения (i) уравнение (ii) (с λ₀ = 1), получаем

Аналогично y = z или х = 1/2, и х = z или y = 1/2.

4° Исследование. Если одно из чисел, скажем z, равно 1/2, то f₀ (х, y, 1/2) = 1/4 < 7/27. Если же ни одно из чисел не равно 1/2, то имеется единственная стационарная точка х̂ = ŷ = ẑ = 1/3 и f₀ (1/3, 1/3, 1/3) = 7/27. Наконец, если решение имеет нулевую компоненту, скажем, х̂ = 0, то 0 ≤ f₀(0, y, z) = yz ≤ 1/4. Ответ: максимум 7/27 достигается при х̂ = ŷ = - ẑ = 1/3, минимум, равный нулю, достигается, скажем, при х̂ = ŷ = 0, ẑ = 1.

И еще об одной геометрической задаче^*. С нею связано воспоминание.

^* (Более подробно о ней см. в статье автора, опубликованной в журнале "Квант" 1983, № 1, с. 22 - 25.)

Это было давным-давно, более тридцати лет назад. Руководитель кружка, загадочно усмехнувшись, спросил нас: "Один тетраэдр лежит внутри другого. Может ли сумма его ребер оказаться больше, чем сумма ребер объемлющего тетраэдра?" Сначала это показалось нам совершенно невозможным. Ведь тетраэдр лежит внутри другого, как же что-то у него может оказаться больше? Но на самом деле сумма ребер действительно может оказаться большей у меньшего тетраэдра. На втором туре 16-й Всесоюзной математической олимпиады десятиклассникам была предложена такая задача.

18. Вершины тетраэдра KLMN лежат внутри, на гранях или на ребрах другого тетраэдра ABCD. Докажите, что сумма длин всех ребер тетраэдра KLMN меньше, чем 4/3 суммы длин всех ребер тетраэдра ABCD.

Это интересный пример, когда можно решить проблему, фактически не приступая к ее стандартному исследованию, ибо слишком многое прояснится сразу после формализации.

Тетраэдр ABCD - это выпуклое замкнутое ограниченное множество. Обозначим его буквой X. В принципе, X можно задать системой из четырех неравенств: X = {х = (х₁, х₂, х₃)| <х, аⁱ> ≤ α_i, i = 1,2, 3,4},(<х, y> - скалярное произведение х и y).

Наша задача формализуется так:

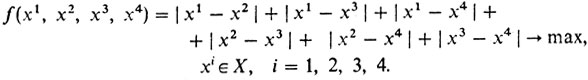
Здесь х^k = (х^k₁, x^k₂, x^k₃), l = 1, 2, 3, 4 - точки в трехмерном пространстве, a |х - y| - расстояние в нем от х до y.

Функция f - непрерывная функция 4 × 3 = 12 переменных. Тетраэдр X - замкнутое ограниченное множество, задаваемое четырьмя неравенствами. По теореме Вейерштрасса решение задачи существует. Пусть оно есть (х̂₁, х̂₂, х̂₃, х̂₄). Из строгой выпуклости f(вытекающей - продумайте - из свойств функции расстояния от фиксированной точки до данной) сразу вытекает, что точки х̂ⁱ необходимо должны совпадать с вершинами X. Действительно, если, скажем, х̂¹ - не вершина, то существует такой отрезок [y, z], где y и z - точки из X и х̂¹ = (y + z)/2. Но тогда по свойству строго выпуклой функции

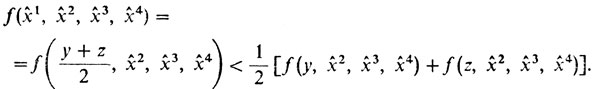
Но отсюда следует, что в одной из точек (y, х̂², х̂³, х̂⁴) или (z, х̂², х̂³, х̂⁴) функция f имеет большее значение, чем в f(х̂¹, х̂², х̂³, х̂⁴). Получилось противоречие.

А теперь остается лишь несложный перебор. Обозначим через P_KLMN периметр тетраэдра KLMN, а через P_ABCD - периметр тетраэдра ABCD.

Если все точки К, L, М и N различны, то тетраэдр KLMN совпадает с ABCD, и все ясно, ибо

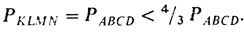
Пусть не более двух вершин тетраэдра P_KLMN совпадают, скажем, К = L = А. Тогда имеются две возможности:

1) две другие вершины тоже совпадают, скажем, М = N = В, и тогда из неравенства треугольника

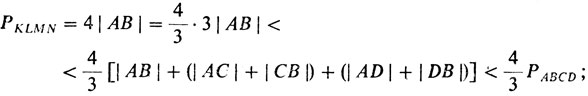
2) вершины М и N различны, скажем, М = В, N = С; тогда из неравенств треугольника следует:

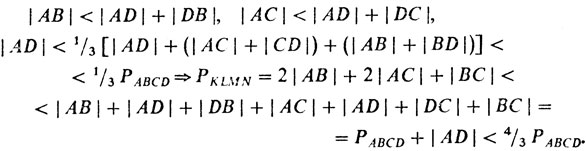
Если же три вершины совпадают, скажем, K = L = M = А, N = В, то из неравенства п. 1) получаем P_KLMN = 3 |АВ| < 4|АВ| < 4/3 Р_ABCD. Задача решена.

Нетрудно понять, что число 4/3 в условии задачи уменьшить нельзя.

Оно достигается для вырожденного тетраэдра ABCD, у которого три вершины - А, В и С - совпадают (скажем, с A) (и тогда P_A'BCD = 3|AD|, а у тетраэдра KLMN две вершины совпадают с А, а две - с D (и тогда P_KLMN = 4|AD|).