Рассказ двенадцатый. Экстремумы функций многих переменных. Принцип Лагранжа

Можно высказать следующий общий принцип. Если ищется максимум или минимум некоторой функции многих переменных при условии, что между этими переменными имеется связь, задаваемая одним или несколькими уравнениями, нужно прибавить к функции, экстремум которой мы ищем, функции, задающие уравнения связи, умноженные на неопределенные множители, и искать затем максимум или минимум построенной суммы, как если бы переменные были независимы. Полученные уравнения, присоединенные к уравнениям связи, послужат для определения всех неизвестных.

Ж. Лагранж

1. Здесь будет рассказано о том, как решать задачи на экстремум функций многих переменных. Суть дела выражена Лагранжем в словах, поставленных нами в качестве эпиграфа. Для освоения первой части этого рассказа необходимо владеть понятиями "непрерывная функция многих переменных" (рассказ десятый) и материалом первой части предыдущего рассказа.

Пусть f₀,f₁, ..., f_m - функции n переменных х = (х₁ ,..., х_n).

Рассмотрим задачу с ограничениями типа равенств и неравенств

Отметим, впрочем, что в основном у нас будут встречаться задачи с одними лишь равенствами.

Примеры.

Напомним, что (з₂) - это при n = 2 формализация планиметрической, а при n = 3 - классической задачи Кеплера о параллелепипеде максимального объема, вписанном в шар.

(з₄) формализует такую задачу: найти на плоскости точку, сумма квадратов расстояний от которой до трех данных точек была бы минимальной (сравните ее с задачей Штейнера).

Разумеется, не каждая задача типа (з) имеет решение. Однако, как и для функций одного переменного, можно сформулировать теорему (также доказанную Вейерштрассом), которая во многих случаях гарантирует существование решения.

Обозначим совокупность допустимых точек в задаче (з) через С. Иначе говоря, С состоит из трех точек х, для которых

Множество С называется ограниченным, если существует константа А > 0 такая, что |х_i| ≤ A, i = 1, ..., n для любой точки х = (х₁..., х_n) из С. Например, множество х²₁ + ... + х²_n = 1 ограничено, в частности ограничена окружность х₁² + х²₂ = 1, а множество х₁ = х²₂ (парабола) не является ограниченным множеством.

Теорема Вейерштрасса.Пусть в задаче (з) функции f₀,...., f_m непрерывны, а совокупность С допустимых точек в (з) ограничена. Тогда решение обеих задач

и

существует.

Укажем, как и в предыдущем рассказе, на такое

Следствие.Пусть функция f₀(х)(х = (х₁ ,..., х_n)) непрерывна для любого х. Тогда если

то решение задачи без ограничений

существует.

Повторим определение локального экстремума в задаче (з).

Определение 1.Говорят, что точка х̂ = (х̂₁, ..., х̂_n) доставляет локальный минимум (максимум) в задаче (з), если можно указать такое ε > 0, что для всех допустимых точек х = (х₁, ..., х_n), удовлетворяющих неравенству

выполнено неравенство f₀ (х) ≥ f₀ (х̂) (f₀(х) ≤ f₀ (х̂)).

Если (з) задача без ограничений и х̂ доставляет ей локальный экстремум, мы говорим еще, что х̂ доставляет локальный экстремум функции f₀.

Для того чтобы можно было сформулировать основное правило решения задач типа (з), необходимо ввести еще одно понятие.

Пусть функция y = f (х) определена для всех х = (х₁, ..., х_n), для которых выполнены неравенства a_j ≤ х_j ≤ b_j, j = 1, ..., n (совокупность всех таких точек назовем параллелепипедом Π(a₁, b₁;,...,;a_n, b_n) и пусть для точки х₀ = (х₀₁, ..., х_0n) выполнены строгие неравенства

Рассмотрим следующую функцию одного переменного:

Что мы сделали? Мы закрепили все координаты у х₀, кроме j-й, а к j-й координате прибавили число х. Предположим теперь, что функция g_j дифференцируема в нуле.

Определение 2.Производная в нуле функции g_j называется j-й частной производной функции f в точке х₀ и обозначается df(x₀)/dx_j.

Теперь сформулируем две теоремы, которые позволят нам затем описать правило решения задач типа (з).

Сначала рассмотрим задачу (з) без ограничений.

Теорема Ферма.Пусть в точке х̂ существуют все частные производные функции f₀. Если точка х̂ доставляет локальный экстремум (минимум или максимум) этой функции, то

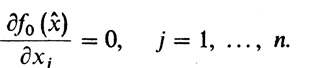(1)

Точки, для которых все частные производные равны нулю, называются стационарными. Соотношения (1) являются, разумеется (как и в случае n = 1), необходимыми условиями.

Приведем пример приложения этой теоремы. Решим задачу (з₁). Решение задачи существует в силу следствия теоремы Вейерштрасса. Обозначим его (х̂, у̂). Имеем

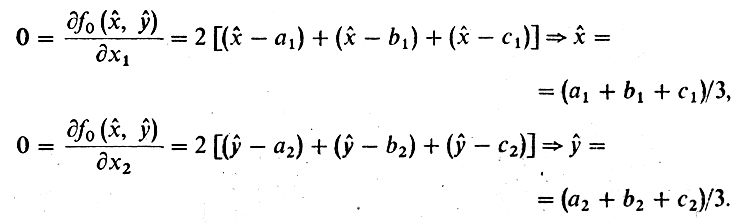
Ответ. (х̂, у̂) есть центр масс треугольника (а₁, а₂), (b₁, b₂), (c₁, c₂).

Теперь рассмотрим общую задачу (з), в которой, правда, неравенства отсутствуют. Составим такую сумму:

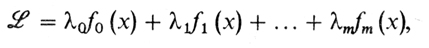
где х = (x₁, ..., x_m), λ = (λ₀, λ₁,....,λ_m)

Эту функцию называют функцией Лагранжа. Числа λ₀, λ₁,....,λ_m называются множителями Лагранжа.

Общий принцип Лагранжа, описание которого вынесено нами в эпиграф, можно коротко выразить так: для решения задачи (з) (с одними равенствами) надо составить функцию Лагранжа, а затем поступить с ней так, как если бы переменные (х₁ ,..., х_n) были независимы (т. е. применить теорему Ферма). Полученные уравнения, а именно уравнения

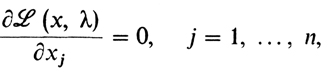(2)

дополненные уравнениями связи

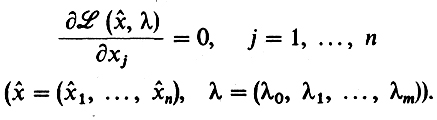(3)

надо решить относительно х₁ ,..., х_n, λ₀, λ₁,....,λ_m и среди этих решений выбрать нужное.

Это правило основывается на следующей теореме.

Теорема (правило множителей Лагранжа).Пусть функции f₀, ...,f_m определены в некотором параллелепипеде Π(a₁, b₁; а₂, b₂; ...; a_n, b_n), содержащем внутри себя точку х̂ = (х̂₁ ..., x̂_n) (a_i x̂_i < b_i, i = 1, ..., n). Пусть далее все функции f_i, i = 0, 1, ..., m, и все частные производные əf_i/əx_j, i = 0, 1, ..., m; j = 1, ..., n непрерывны в этом параллелепипеде. Тогда если допустимая точка х̂ доставляет локальный экстремум (минимум или максимум) в задаче (з) (где неравенства отсутствуют: m' = m), то найдутся числа λ₀, λ₁,....,λ_m, не равные одновременно нулю и такие, что

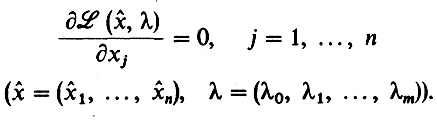
Сделаем теперь несколько замечаний. Отметим, во-первых, что в (2) и (3) имеется n + m уравнений с n + m + 1 неизвестным. Но надо иметь в виду, что множители Лагранжа можно умножать на любую константу, отличную от нуля.

Таким образом, всегда можно домножить так, чтобы один из множителей Лагранжа равнялся единице. Тогда в (2) - (3) число уравнений фактически равно числу неизвестных.

Далее. Уравнения (2) наиболее содержательны, если λ₀ ≠ 0. Ведь если λ₀ = 0, то уравнения (2) отражают лишь вырожденность ограничений и не связаны с функцией, экстремум которой ищется. Но вообще-то заранее считать, что λ₀ отлично от нуля (как это делает Лагранж - см. эпиграф), нельзя. Приведем пример, показывающий, что правило множителей Лагранжа при дополнительном допущении λ₀ ≠ 0 может стать неверным.

Пример. Рассмотрим задачу (см. рис. 48):

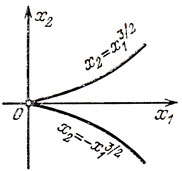
Рис. 48

Из рисунка видно, что единственным решением задачи является точка х̂ = (0, 0). Попробуем теперь составить функцию Лагранжа с λ₀ = 1 и применить алгоритм Лагранжа:

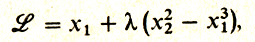
откуда

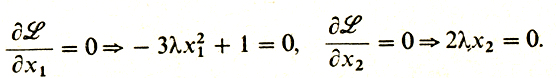
Уравнение связи имеет вид х²₂ - x³₁ = 0. Написанные уравнения, как легко видеть, не совместны.

Правило множителей Лагранжа позволяет дать следующий рецепт поиска решений задачи (з) с равенствами. Разобьем его на те же 4 этапа.

1 этап - формализация задачи. Требуется привести (разумеется, если это возможно) задачу к виду (з) с m' = m.

2 этап - применение принципа Лагранжа, т. е. составление системы уравнений

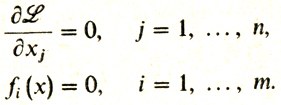
3 этап состоит в нахождении всех стационарных точек. При этом бывает полезно сначала выяснить вопрос о том, может ли λ₀ равняться нулю или нет.

4 этап состоит в переборе всех стационарных точек и выборе тех, где функция f₀ имеет минимальное (максимальное) значение.

Этот рецепт решения мы коротко называем принципом Лагранжа.

Из сформулированных теорем следует, что если (в задаче без неравенств) совокупность допустимых точек ограничена и все функции f₀,...,f_m непрерывны и непрерывны все частные производные əf_i/əx_j, i = 0,...., m, j = 1, ..., n, то описанное правило приведет к решению задачи.

Искусству дифференцировать функции многих переменных заново обучать не надо: ведь все сводится к дифференцированию функций одного переменного. Теперь уже можно было бы перейти к решению задач. Но мы потратим еще некоторое время на обсуждения.

2. Здесь так же, как и в предыдущем рассказе, уделим место некоторым объяснениям.

Теорему Ферма в многомерном случае нет нужды специально объяснять, ибо она тривиально выводится из одномерного случая. Действительно, пусть функция f₀(х₁,..., х_n) имеет локальный экстремум в точке (х̂₁ ,..., х̂_n). То есть функция g_j(x) (по типу той, которая была определена в п. 1)

должна иметь минимум в нуле. Но тогда по одномерной теореме Ферма, которая подробно освещалась в предыдущем рассказе, получаем

Но по самому определению j-й частной производной как раз и получается, что

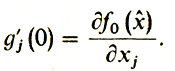
Сопоставляя эти два равенства и произвольность j, приходим к теореме Ферма:

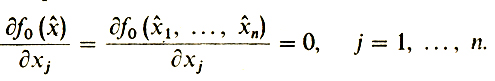
Теперь нам предстоит разобраться в правиле множителей Лагранжа. Начнем наши объяснения с простейшей ситуации, когда, во-первых, n = 2, m = 1, а во-вторых, когда ограничение задается линейным соотношением. Иначе говоря, будем рассматривать следующую задачу:

График y = f₀(x₁, х₂) можно мыслить себе (вспомните, что говорилось в десятом рассказе) как ландшафт горной местности. Соотношение f₁(х₁, х₂) = a₁x₁ + а₂х₂ - b = 0 задает на плоскости прямую. Можно представить себе, что в горной местности прокладывают линию электропередачи по траектории, которая на карте имеет вид прямой. Спрашивается, где будет самая высокая точка трассы?

Вспомним, как горы изображают на картах. Там наносят линии одинаковой высоты, линии уровня. Задумаемся над тем, как должны быть расположены друг относительно друга трасса электропередачи и линия уровня нашей горы в точке наивысшего подъема.

Ясно, что трасса в этой точке не может пересекать линию уровня. Если трасса пересекает ее, то она проходит из области меньших значений высоты в область ее больших значений, и значит, в точке пересечения максимума высоты быть не может. Вывод: в точке максимума высоты трасса должна касаться линии уровня.

Теперь посмотрим на функцию f₁(х₁, х₂) = a₁x₁ + а₂х₂ - b. Ее частные производные

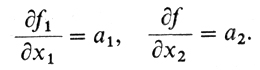
Вектор (а₁, а₂) перпендикулярен трассе и вообще любой линии уровня функции f₁ (х₁, х₂). Это ясно из геометрического смысла уравнения а₁x₁ + а₂х₂ = b. Однако оказывается, что этот факт верен всегда. А именно, если f(х₁, х₂) - любая непрерывная функция, у которой ее частные производные также непрерывны, то вектор

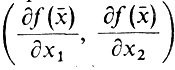
перпендикулярен касательной к линии уровня f(х) = f(х̄).

Но ведь трасса тоже касательна к линии уровня в точке максимума высоты. Из всего сказанного и вытекает, что оба вектора

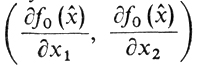
перпендикулярны трассе и, следовательно, пропорциональны, т. е.

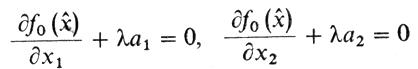
или

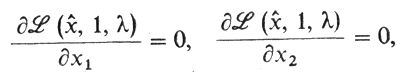
где

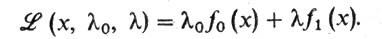
В этой частной ситуации мы пришли к правилу множителей Лагранжа.

Пусть теперь функция f₁ - не обязательно аффинная, но у нее имеются непрерывные частные производные. Снова рассмотрим семейство линий уровня

Допустим, что в некоторой части плоскости через каждую точку проходит одна и лишь одна кривая каждого из семейств. Предположим, что в х̂ = (х̂₁, х̂2) задача имеет решение. Тогда все точки кривой l₀, задаваемой уравнением

обязаны лежать "по одну сторону" от кривой l₁ задаваемой уравнением

т. е. эти кривые должны не пересекаться, а касаться. Мы объяснили, что если в точке х̂ на кривой l₁ функция f₀ имеет экстремальное значение, то кривая f₀ касается кривой l₁.

Еще раз напомним о том, что вектор (df₀ (х̂)/dx₁, df₀ (х̂)/dx₂) перпендикулярен кривой l₀, а вектор (df₀(x̂)/dx₁, df₀(x̂)/dx₂) перпендикулярен кривой l₁. Если эти кривые касаются, то данные векторы должны быть пропорциональны.

Пропорциональность этих векторов и утверждается в правиле множителей Лагранжа (с λ₀ = 1).

Доказать принцип Лагранжа (т. е. правило множителей Лагранжа) в этой книге мы не сможем. Однако некоторые пояснения, касающиеся доказательства его, будут даны в четырнадцатом рассказе.

В начале рассказа была поставлена общая задача, когда имеются и равенства, и неравенства. А дальше речь шла уже об одних лишь равенствах. Как видоизменяется принцип Лагранжа в общем случае? Вернемся к задаче (з), которая была поставлена вначале, и допустим, что все функции f₀(х), ...,f_m(x) удовлетворяют условиям сформулированной выше теоремы о правиле множителей Лагранжа. Тогда, если допустимая точка х̂ доставляет локальный минимум в задаче (з), то найдутся числа λ₀, ₁,...,λ_m не равные одновременно нулю и такие, что

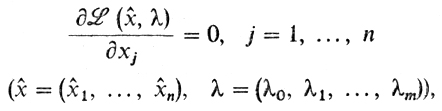
кроме того, удовлетворяются условия не отрицательности множителей Лагранжа при функционале и неравенствах λ₀ ≥ 0, λ_m'+1 ≥ 0,..., λ_m ≥ 0 и выполняются следующие условия (так называемые условия дополняющей не жесткости):

Условия дополняющей не жесткости означают, что множитель Лагранжа λ_j может быть отличен от нуля только на "активном" ограничении, когда в точке экстремума ограничение типа неравенства на самом деле является равенством: f_j (х̂) = 0, j = m' + 1, ..., m.

Что же изменилось? Во-первых, здесь "экстремум" заменился на "минимум". При неравенствах небезразлично, какой тип экстремума рассматривается. В случае задачи на максимум или при наличии ограничений вида f_j > 0 для применения только что сформулированного результата необходимо сначала преобразовать задачу к виду (з), заменив, если это нужно, некоторые из f_j, j = 0, m' + 1, ..., m на - f_j. Во-вторых, добавилось условие не отрицательности, в-третьих - условие дополняющей не жесткости.

При решении задач в этой книге нам не придется применять только что сформулированную теорему. Но роль ее и ей подобных теорем очень значительна. В первом рассказе мы как-то сказали, что старые методы оказались недостаточными для решения многих экономических проблем. Теперь об этом можно сказать конкретнее.

Вспомним транспортную задачу, о которой разговор заходил уже дважды. В ее формализации участвуют неравенства, без них формализировать ее затруднительно. Но раньше задач с неравенствами не рассматривали. То дополнение к правилу множителей Лагранжа, которое только что было сделано, появилось лишь сорок (а не двести пятьдесят) лет тому назад. И еще одно. Выяснилось, что в экономических задачах очень часто минимизируемые функции и ограничения выпуклы или даже линейны.

Пришлось специально заняться изучением выпуклых функций и выпуклых экстремальных задач. И мы уделим этому некоторое внимание.

3. Выпуклые функции и выпуклые задачи. О выпуклых функциях одного переменного мы мельком уже сказали. Выпуклые функции нескольких переменных определяются совершенно аналогично. Функция f(х) = f(х₁ ,..., х_n) называется выпуклой, если для любых точек х и х' и любого α, 0 ≤ α ≤ 1, имеет место неравенство Иенсена

Примерами выпуклых функций являются прежде всего линейные и аффинные функции. Отметим также "функцию расстояния" от точки до нуля

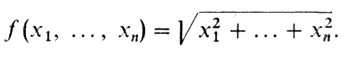
Функцию y = f (х) называют строго выпуклой, если в неравенстве Иенсена при х ≠ х' и 0 < α < 1 имеет место строгое неравенство

Функции y = х², y = √(h² + х²) и x²₁ + х ²₂ строго выпуклы, а функция y = |х| или функция расстояния - не строго выпуклы. Нетрудно понять, что если функция y = f (х) строго выпукла и достигает в точке х̂ своего минимума, то этот минимум единствен.

Уже было сказано, что не всякая функция является дифференцируемой, и дважды обсуждался пример: y = |х|. Эта функция выпукла и не дифференцируема в нуле. Функция расстояния также дифференцируема всюду, кроме нуля, где она не является дифференцируемой. Однако если выпуклая функция дифференцируема и в некоторой точке ее производная равна нулю, то в этой точке функция достигает своего абсолютного экстремума. И даже более того: график любой выпуклой функции лежит "выше" любой своей касательной плоскости.

Отмеченное обстоятельство очень важно: для выпуклых дифференцируемых функций теорема Ферма является достаточным условием экстремума! Вот одна из причин того, что теория выпуклых экстремальных задач имеет такой завершенный характер.