Рассказ одиннадцатый. Экстремумы функций одного переменного

Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад.

И. Ньютон

Этот и следующий рассказы построены одинаково. Они состоят из двух частей. В первой части излагается сам метод решения задач без доказательств, хотя и с некоторыми объяснениями и комментариями. Во второй части проводятся точные определения и некоторые доказательства. Для освоения первой части необходимо владеть лишь следующими понятиями: "предел", "непрерывная функция" и "производная".

1. Здесь будет рассказано о методе отыскания решения таких задач на экстремум функций одного переменного:

В (з) а и b могут принимать и бесконечные значения. Таким образом, речь будет идти об экстремумах функции /0 на конечном отрезке, на луче или на совокупности всех вещественных чисел.

Примеры.

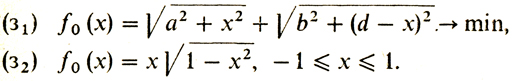
Напомним, что (з₁) - это формализация задачи Герона, (з₂) - формализация планиметрической задачи Кеплера (обе задачи были формализованы в рассказе десятом).

Заметим, что не всякая задача имеет решение. Например, мы уже рассматривали такую задачу без ограничений:

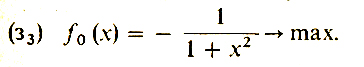
Функция f₀(х) ≤ 0, и нет такой точки x̄, где f₀(х) = 0.

С другой стороны, если взять точки х_n = n, n = 1, 2, ..., то f₀ (х_n) → 0. Отсюда следует, что максимума в (з₃) не существует, т. е. нельзя указать такую точку x̂, что f₀(х) ≤ f₀(x̂) для всех x.

Итак, максимумы и минимумы существуют не всегда. Однако имеется замечательная теорема Вейерштрасса, которая дает в огромном числе случаев гарантию существования решения.

Теорема Вейерштрасса.Пусть f₀(x) - непрерывная функция на конечном отрезке [a, b]. Тогда решения обеих задач

и

существуют.

Из этой теоремы немедленно следует, что решение задачи (з₂) существует. А про (з₁) этого сказать пока нельзя, ибо там функция рассматривается на всей прямой, а не на конечном отрезке.

Из теоремы Вейерштрасса выводится такое следствие, которое позволит, в частности, доказать существование и в (з₁).

Следствие.Пусть f₀ непрерывна на всей прямой. Тогда, если lim_x→∞ f₀(x) = lim_x→-∞ f₀(х) = ∞, решение задачи без ограничений

существует.

У нас еще встретятся случаи, когда f₀ непрерывна на луче вида а ≤ х < ∞ или а < х < ∞. Следовательно, если в первом случае lim_x→∞ f₀ (х) = ∞, а во втором lim_x→a f₀ (х) = lim_x→∞ f₀ (х) = ∞, то функция f₀ достигает своего минимума на соответствующем луче.

Для отыскания решения задачи (з) будем использовать прием, впервые примененный Ферма.

Но сначала напомним одно определение, о котором говорилось в предыдущем рассказе. Пусть функция f₀ определена на отрезке а ≤ x ≤ b в х̂ - точка из этого отрезка. Говорят, что точка х̂ доставляет локальный минимум (максимум) в задаче (з), если можно указать такое ε, что для всех точек х из отрезка [а, b], для которых |х - х̂| < ε, выполнено неравенство f0(х) ≥ f₀(x̂)(f₀(x) ≤ f₀(x̂)).

Иногда мы говорим проще: х̂ доставляет локальный экстремум функции f₀.

Имеет место

Теорема Ферма.Пусть функция f₀ является дифференцируемой в точке х̂. Тогда, если точка х̂ доставляет локальный экстремум (минимум или максимум) этой функции f₀, то f₀ (х) = 0.

Точки, для которых f'₀ (х) = 0, называются стационарными. Стационарные точки совместно с концевыми, точками называются критическими.

Соотношение f'₀ (х̂) = 0 является лишь необходимым условием экстремума. Например, для функции f₀ (х) = х³ точка х = 0 является стационарной, но ни локального максимума, ни локального минимума не доставляет.

Теорема Ферма позволяет дать следующее правило поиска решений одномерных задач. Разобьем его на 4 этапа.

1 этап - формализация задачи. Требуется привести (разумеется, если это возможно) стоящую перед вами задачу к виду

2 этап состоит в выписывании необходимого условия f'₀(x) = 0.

3 этап состоит в нахождении всех стационарных точек.

4 этап состоит в переборе всех критических значений функции f₀ и выбора минимального (максимального) среди них.

Из теорем Вейерштрасса и Ферма следует, что если функция f₀ удовлетворяет на [а, b] теореме Вейерштрасса (или следствиям из нее) и, кроме того, если она дифференцируема во внутренних точках х отрезка [a, b] (когда а <х < b), то описанное правило приведет к решению задачи.

Выделим отдельно следующий факт, которым в основном и будем пользоваться: если отрезок [a, b] конечен, функция f₀ непрерывна на [а, b] и дифференцируема во внутренних точках х, а < х < b, то решение находится среди критических точек.

Таким образом, для применения описанного правила требуется умение дифференцировать. Для облегчения этой процедуры приведем таблицу производных основных функций, несколько часто употребляемых формул, а также напомним важнейшее правило нахождения производной сложной функции.

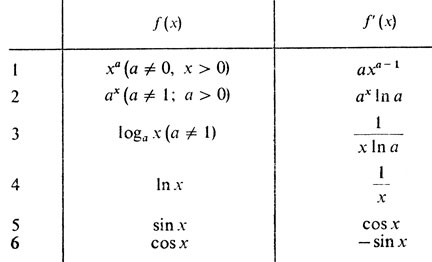
Таблица производных

Кроме этой таблицы, полезно помнить следующие формулы:

7.

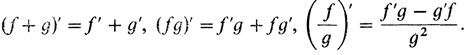
И еще одно. Очень часто функции, с которыми нам придется сталкиваться, имеют вид h(x) = f(g(x)). Нужно запомнить и научиться пользоваться следующей формулой для производной сложной функции:

8.

Пример, h (х) = √(а² + х²). Здесь h (х) = f(g (x)), где f(u) = √u = u^1/2, g(х) = а² + х². Пользуясь формулой 1 таблицы и формулами 7 и 8, получаем

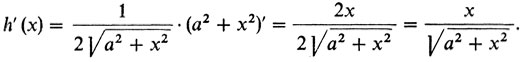
В заключение этого пункта скажем несколько слов о выпуклых функциях. Их значение в теории экстремальных задач велико, и нам придется не раз затрагивать эту тему. Сейчас дадим определение выпуклых функций одного переменного.

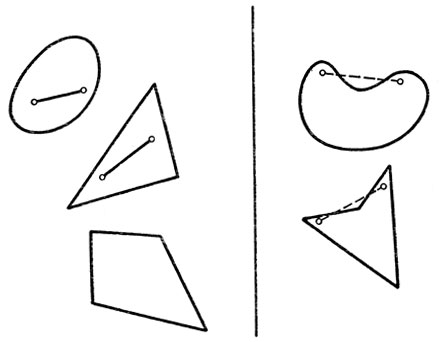
Рис. 45

С самим понятием выпуклости мы сталкиваемся еще в школе. Напомним, что фигура называется , выпуклой, если вместе с любыми двумя своими точками она содержит весь отрезок, соединяющий эти точки. Любой треугольник как часть плоскости - выпуклая фигура, среди четырехугольников встречаются и не выпуклые (рис. 45).

Можно дать три равносильных определения выпуклой функции. Приведем их. Функция y = f(x) называется выпуклой, если для любой хорды, соединяющей две точки графика этой функции, ее график в промежуточных точках лежит ниже этой хорды; или: множество точек плоскости, лежащее выше графика функции y = f(х), является выпуклым; или: для любых чисел x₁ и х₂ и любого α, 0 ≤ α ≤ 1 имеет место следующее неравенство (неравенство Иенсена):

Примеры выпуклых функций доставляют прежде всего линейные функции, функции вида y = bх + с (аффинные) и квадратные трехчлены y = ах² + bх + с, у которых а > 0. Среди функций y = |х|^р выпуклы лишь те, у которых р ≥ 1. Функция √(h² + х²) выпукла при любых И. Не все выпуклые функции всюду дифференцируемы. Например, функция y = |х| не дифференцируема в нуле. Но если выпуклая функция дифференцируема, то ее производная является возрастающей функцией.

2. В первой части этого рассказа было описано правило решения задач. Это правило нетрудно запомнить, и сразу можно решать задачи. (Что мы и будем делать в тринадцатом рассказе.) Но многим, наверное, захочется все-таки понять, откуда взялось это правило. Об этом и будет рассказано здесь, причем дважды, и вот почему.

Те, кто увлекаются чтением научной и научно-популярной литературы, разделяются, как мне кажется, на две группы. Одну группу образуют читатели (и их большинство), которые стремятся постичь лишь основные идеи. Они удовлетворяются не вполне строгим, но выразительным изложением и не бывают в претензии, если заметят, что при изложении были опущены некоторые, по впечатлению - несущественные, детали. В первой части этого пункта и аналогичного пункта следующего рассказа я буду ориентироваться на эту группу читателей.

Но не следует забывать и о тех, кого не удовлетворяет лишь описание общих идей, кому захочется разобраться в сути дела, по возможности, до конца. Заключительная часть этого пункта написана в расчете на вторую группу читателей. В этой части мы стремимся быть возможно точными и краткими.

Представьте себе: вы едете по прямолинейному шоссе (рис. 46). В каждый момент времени ваша машина находится на определенном расстоянии от какого-то начального пункта. Таким образом, местоположение машины может быть выражено в каждый заданный момент t одним числом s(t). Получается функция от времени: s(t) есть расстояние от машины до начального пункта в момент времени t.

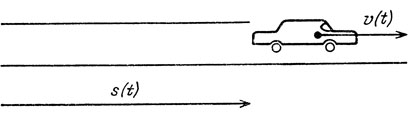
Рис. 46

Теперь посмотрим на спидометр. Он показывает скорость. Скорость машины в момент t обозначим v (t). Из курсов физики и математики мы знаем, что скорость - это производная пути по времени:

(Говорят, что лорд Кельвин, один из крупнейших физиков прошлого века, утверждал нечто обратное. Он говорил примерно так: "Не морочьте мне голову с вашей математикой: производная - это скорость"!)

Если скорость в данный момент не равна нулю - пусть для определенности она положительна, как это изображено на рис. 46,-то в следующие моменты мы удалимся от начального пункта на еще большее расстояние, а в предшествующие моменты мы были чуть ближе к начальному пункту. Таким образом, функция расстояния s(t) в данный момент не может иметь ни максимума, ни минимума. И следовательно, в точке максимума или минимума скорость обязана равняться нулю: в этот момент мы, по словам Ньютона, не течем "не вперед, ни назад". Но в этом как раз и состоит теорема Ферма.

Теперь о том же самом скажем поточнее. Прежде всего, необходимо дать точное определение производной. Можно было бы воспользоваться определением, которое проходят в школе, но тогда у нас возникли бы сложности в следующих рассказах, когда речь зайдет о производных функций многих переменных. Поэтому здесь будет дано определение, которое одинаково пригодно и в конечномерном, и (снова пока по секрету) в бесконечномерном случаях.

Итак, что значит: функция f дифференцируема в данной точке х₀ (или, что то же, - имеет производную в точке х₀)? Если не прибегать к формулам, то можно сказать так: это означает, что функция f(х₀ + х) - f(х₀) хорошо аппроксимируется линейной функцией. А если точно, это означает следующее.

Определение.Говорят, что функция y = f(х), определенная на отрезке [а, b], содержащем внутри себя точку х₀ (а < х₀ < b), дифференцируема в точке х₀ (или, что то же,- имеет производную в точке х₀), если существует такая линейная функция y = kx, что

где lim_x→0 |r(х)|/|х| = 0 (или, как иногда говорят, r(х)/х есть величина бесконечно малая).

Из нашего определения немедленно вытекает, что

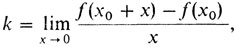
и, таким образом, число k, участвующее в определении, определяется однозначно. Оно и называется производной f в точке х₀ и обозначается f'(х₀).

Геометрический смысл производной состоит в том, что прямая, являющаяся графиком функции y = f'(x₀)(x - х₀) + f(х₀) (проходящая через точку (х₀,f(х₀)) с угловым коэффициентом, равным производной f'(х₀)), является касательной к графику Функции y = f(x) (рис. 47).

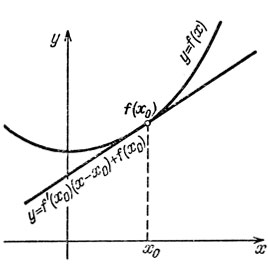
Рис. 47

Пример 1. Квадратный трехчлен y = ах² + bх + с всюду дифференцируем и его производная в точке х₀ равна 2ах₀ + b. Проверим это на функции f(х) = х². Имеем

При этом 2х₀х - линейная функция, r(х) = х², и значит, lim_x→0 |r(х)|/|х| = lim_x→0 х²/| х | = 0, т. е. f дифференцируема в х₀ и f' (х₀) = 2х₀.

Из списка, приведенного в п. 1, видно, что элементарные функции а^х (а ≠ 0), sin х, cos х, log_a х дифференцируемы всюду, где они определены.

Приведем пример функции, которая в некоторой точке не дифференцируема.

Пример 2. Функция y = |х| не дифференцируема в нуле. Действительно, возьмем любую линейную функцию y = kx. Пусть для определенности k ≤ 0. Положим

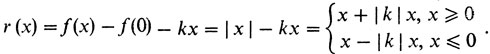
Значит, lim_x→0,x≥0 |r(х)|/|х| = 1 + |k| ≠ 0; функция не дифференцируема. Случай k > 0 аналогичен.

Теорема Ферма.Пусть функция f₀(х) определена на некотором отрезке [a, b], содержащем внутри себя точку х (а < х̂ < b). Пусть при этом она является дифференцируемой в точке х̂. Тогда, если точка х̂ доставляет локальный экстремум (минимум или максимум) этой функции, f'₀ (х̂) = 0.

Точное определение локального экстремума было дано в п. 1.

Доказательство. Предположим, что f'₀ (х₀) = k ≠ 0, и докажем, что х̂ не является локальным экстремумом. Допустим, k > 0. По определению предела из того, что lim_x→0 |r(х)|/|х| = 0 (где r(х) = f₀ (х̂ + х) - f₀ (х̂) - kx) следует, что найдется δ > 0 такое, что если |х| < δ, то |r(х)| <(k/2)|х|.

Но тогда для х > 0 r(х) ≥ -k/2 x и следовательно,

а для х < 0 r(х) ≤ k/2 x, и следовательно,

т. е. слева от х̂ значения f₀ меньше f₀(х), а справа - больше. Это значит, что х̂ не является ни максимумом, ни минимумом. Теорема доказана.

Геометрический смысл теоремы Ферма: в точке максимума или минимума касательная должна быть горизонтальна. Подчеркнем еще "вычислительный" смысл экстремума, о котором говорит Кеплер (см. эпиграф к шестому рассказу). Возьмем для примера функции f₁(x) = x и f₂(x) = х₂. У первой функции нет экстремума в нуле, а у второй - есть. Если придать приращение аргументу, то в первом случае функция смещается на такую же величину, а во втором - "изменения нечувствительны". Скажем, если х = 0,01 (а это еще можно изобразить на миллиметровой бумаге), то f₂(х) = 0,0001, а это уже совершенно "нечувствительно".

Вот так обстоит дело с теоремой Ферма. Некоторые сведения исторического характера мы отложим до четырнадцатого рассказа.

Переходим к теореме Вейерштрасса о существовании экстремума непрерывной функции на конечном отрезке. Вследствие того, что любой отрезок можно перевести в единичный отрезок [0, 1], далее всюду будем рассматривать именно его.

Предварительно докажем следующую лемму о монотонной последовательности чисел.

Лемма. Монотонная последовательность чисел из единичного отрезка имеет предел в этом отрезке.

Иначе говоря, если задана бесконечная последовательность чисел {x₁ ..., x_n, ...}, обладающих теми свойствами, что, во-первых, они из единичного отрезка, т. е. 0 ≤ х_n ≤ 1, n = 1, 2,..., а во-вторых, что они монотонны,- для определенности, пусть они монотонно возрастают, т. е. х₁ ≤ х₂ ≤ ... ≤ х_n ..., то существует число х₀ из единичного отрезка (0 ≤ х₀ ≤ 1) такое, что lim_n↓∞ х_n = х₀.

Прежде чем доказывать лемму, необходимо сказать, что такое число из единичного отрезка. Числа из единичного отрезка представляются бесконечными десятичными дробями 0, n₁n₂n₃ ..., где n_i - одно из десяти чисел 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Доказательство. Возьмем первые числа после запятой десятичного представления чисел последовательности {х₁ ... ..., х_n, ...}. Получим (вследствие монотонности нашей последовательности) возрастающую последовательность целых чисел, каждое из которых не меньше нуля и не больше девяти. Какое-то из этих целых чисел, обозначим его n₁ должно повториться бесконечное число раз. Возьмем тот наименьший номер N₁ когда это целое число встретится у нас впервые. Тогда чисел, больших пи в нашей последовательности уже не встретится, так как если бы нашлось какое-то большее число, то из-за монотонности этой последовательности число далее уже не встретилось бы.

Далее возьмем вторые числа после запятой последовательности {x_N1, x_N1+1 ...}. Снова получим возрастающую последовательность целых чисел, каждое из которых не меньше нуля и не больше девяти, и снова возьмем число n₂, которое встретится бесконечное число раз, и номер N₂, когда оно появится впервые. Далее поступаем аналогично. В итоге приходим к десятичной дроби 0, n₁n₂... Она представляет собой некоторое число х₀ из единичного отрезка. Кроме того, у нас возникла последовательность номеров N₁ ≤ N₂ ≤... ≤ N_s..., где числа n_s появляются впервые. Из построения ясно, что для любого n = 1, 2, ... выполнено неравенство

С другой стороны, если n ≥ N_s, то

Написанные соотношения означают, что lim_n→∑ х_n = х₀. Лемма доказана.

Теорема Вейерштрасса.Непрерывная функция на конечном отрезке принимает свое максимальное и минимальное значение.

Напомним, что функция y = f(х), определенная на отрезке [а, b], содержащем точку х₀ (а ≤ х₀ ≤ b ) называется непрерывной в точке х₀, если для любого ε > 0 можно указать δ > 0 такое, что из неравенств |х - х₀| < δ, а ≤ х ≤ b последует неравенство |f(х) - f(х₀)| < ε. Из этого определения сразу следует, что если f непрерывна в точке х₀ и {х₁, ..., х_n, ...} - последовательность, сходящаяся к х₀ (lim_n∞ х_n = х₀), то последовательность {f(x₁), ..., f(х_n), ...} сходится к

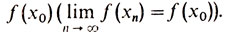
Функция, непрерывная в каждой точке отрезка, называется непрерывной на отрезке. Говорят, что в точке х₀ функция y = f(х), заданная на [a, b] принимает на нем свое максимальное (минимальное) значение, если f(х₀) ≥ f(х) (f(х₀) ≤ f(х)) для любого х из отрезка [а, b].

Теперь можно перейти к доказательству теоремы Вейерштрасса. Будем доказывать ее для максимума.

Доказательство. Пусть функция y = f(х) определена и непрерывна на единичном отрезке [0, 1]. Возьмем два отрезка Δ₁ = [а₁, b₁] и Δ₂ = [а₂, b₂], содержащиеся в [0, 1]. Мы скажем, что отрезок Δ₁ лучше Δ₂, если найдется такая точка x̄ из Δ₁ что f(х̄) > f(х) для любого х из Δ₂.

Разобьем отрезок Δ⁰ = [0, 1] на два равных отрезка Δ¹₁ = [0, 1/2] и Δ¹₂ = [1/2, 1].

Выберем из отрезков Δ¹₁ и Δ¹₂ лучший; если ни один из них не лучший, возьмем любой из этих отрезков. Левую точку выбранного отрезка Δ¹ обозначим x₁.

В силу нашего выбора для всякой точки х, не лежащей в Δ¹, найдется точка х̄ из Δ¹, в которой f(х̄) ≥ f(х).

Действительно, если Δ¹ - лучший, то все очевидно, а если он не лучший и точка х̄ не найдется, то это означает, что другой отрезок лучший, что противоречит нашему выбору.

Далее разобьем отрезок Δ¹ на два равных отрезка Δ²₁ и Δ²₂ и снова выберем либо лучший, либо любой, если лучшего нет. Левую точку выбранного отрезка Δ² обозначим х₂. Снова в силу нашего выбора для всякой точки х̄, не лежащей в Δ², найдется точка х̄ из Δ², в которой f(х̄) ≥ f(х) (продумайте).

Далее будем поступать аналогично. В итоге получаем монотонную последовательность {х₁, ..., х_n, ...} из [0, 1]. По лемме она имеет предел, который обозначим х₀. Докажем, что f(x₀) ≥ f(x) для всякого х из [0, 1]. Действительно, допустим, что существует точка х̃, в которой f(х̃) > f(х₀). Выберем δ столь малым, чтобы |х₀ - х̃| > δ и из неравенств |х - х0| < δ, 0 ≤ х ≤ 1 следовало бы, что f(х) < f(x̃).Длины отрезков Δⁿ равны 2^-n, а их левые концы х_n стремятся к х₀. Значит, в какой-то момент весь отрезок Δⁿ окажется внутри интервала (х₀ - δ, х₀ + δ). Но тогда, с одной стороны, в нем найдется х̄ такое, что f(х̄) ≥ f(х̃), а, с другой стороны (так как |х̄ - х0| < δ), f(х̄) < f(х̃). Пришли к противоречию. Теорема доказана.

Следствие из теоремы (сформулированное в начале рассказа) доказывается совсем просто.

Найдем такое число А, чтобы для |х| ≥ А выполнялось неравенство f₀ (х) ≥ f₀ (0). По теореме Вейерштрасса найдется точка х₀ из отрезка [ - А, А] такая, что f(х₀) ≤ f(х) для любого х из отрезка [-А, A]. Ясно, что f(х₀) ≤ f(0). Но если |х| > A, то f(x) ≥ f(0) ≥ f(х₀). Значит, f(х) ≥ f(х₀) для любого х, что и требовалось получить. Два других случая доказываются так же просто.

Таким образом, мы привели доказательство всех фактов, о которых речь шла в п. 1.