Рассказ десятый. Что такое экстремальная задача?

В первой части этой книги мы перерешали множество задач на максимум и минимум. Некоторые из них были поставлены очень давно, сотни лет назад, и в их исследованиях приняли участие величайшие математики прошлого - Евклид, Архимед, Кеплер, Ферма, Бернулли, Лейбниц, Ньютон... Эти исследования были совсем не похожи друг на друга, а цель иногда достигалась после долгих блужданий.

Эпиграфом к этой части поставлены слова Даламбера. Вдумаемся в них. Спросим себя: возможно ли изыскать способ решения всех задач (и даже тех, о которых рассказывалось в первой части) одним и притом простым способом?

То, что не может быть единого простого рецепта решения всех на свете проблем, ясно каждому. (Даламбер, кстати, говорил лишь о задачах динамики.) Может показаться сомнительной и возможность такого единого приема, который позволил бы решить хотя бы все задачи, обсуждавшиеся нами в первой части. Но тем не менее, такой прием имеется, и мы изложим его здесь, во второй части этой книги. С помощью этого (одного и притом простого) приема все задачи первой части будут решены единообразно, стандартно, если хотите - рутинно.

Но сначала нужно позаботиться о единой форме записи условий задач и об общем языке, на котором можно было бы рассуждать о задачах столь разного содержания. Этому посвящен наш рассказ.

Сначала давайте еще раз уточним значения ключевых слов: "максимум", "минимум", "экстремум", "оптимум".

Напомним о двух планиметрических задачах из первой части. Об одной рассказывалось неоднократно, начиная с первого рассказа, о другой говорилось в рассказе пятом.

Задача Герона. Даны две точки по одну сторону от прямой. Требуется на прямой найти такую точку, чтобы сумма расстояний от нее до двух данных точек была минимальна (рис. 1).

Планиметрическая задача Кеплера. Вписать в круг единичного радиуса прямоугольник наибольшей площади.

Эти задачи отличаются друг от друга тем, что в первой надо найти минимум, а во второй - максимум.

Напомним: слова maximum и minimum - латинские. Они значат "наибольшее" и "наименьшее". Еще два слова латинского происхождения часто употребляют, когда говорят про задачи на максимум и минимум. Термин "экстремум" - от латинского extremum, что значит "крайнее" - объединяет понятия максимум и минимум (этот термин предложил использовать французский ученый Дюбуа Реймон). В последние годы вошло во всеобщее употребление прилагательное "оптимальный". Оно происходит от латинского optimus, означающего "наилучший", "совершенный".

Теорию задач на отыскание наибольших и наименьших величин называют или теорией экстремальных задач, или теорией оптимизации. А если проблема состоит в наилучшем воздействии на какие-то процессы и явления, которыми человек может в определенных пределах управлять, то ее относят к разделу теории экстремальных. задач, называемому "оптимальным управлением".

Задачи Герона и Кеплера были чуть выше сформулированы словесно, без формул. То же самое относится и ко всем задачам первой части: в задачах геометрического содержания (изопериметрической, штейнеровской и др.) использовалась геометрическая терминология, в механических (о брахистохроне, ньютоновской) - механическая, в алгебраических (тартальевской, о неравенствах и др.) - алгебраическая. Никаких формул не было. И все это - в порядке вещей. Экстремальные проблемы, возникающие в математике, естествознании или в практических делах, первоначально ставятся без формул, в терминах той области, в которой они возникли. Для того чтобы можно было воспользоваться общей теорией, необходимо осуществить перевод постановок задач со специфического языка на язык математики. Такой перевод называется формализацией.

Проиллюстрируем, как осуществляется формализация на примерах. Начнем с задачи Герона.

Направим ось Ох по заданной прямой, а ось Оy проведем перпендикулярно оси Ох через точку А (рис. 1). Пусть координаты точек А и В оказались такими: А = (0, a), B = (d,b). Возьмем на оси Ох точку D с координатой (х, 0). Тогда сумма расстояний от А до D и от D до В будет равна √(а² + х²) + √(b² + (d - х)²).

Мы пришли к такой задаче: найти наименьшее значение функции

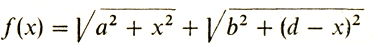
по всем х.

Приведенная нами формализация выглядит очень естественно и как бы напрашивается сама собой. Но, вообще говоря, задача может иметь множество формализаций. Покажем это на примере планиметрической задачи Кеплера.

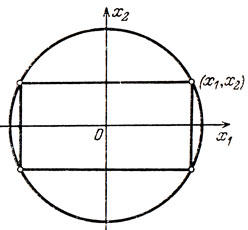
Рис. 44

Направим оси Оx₁ и Ох₂ параллельно сторонам прямоугольника. Единичная окружность описывается уравнениями х²₁ + х²₂ = 1. Пусть (х₁, х₂) - координаты той вершины прямоугольника, которая лежит в первом квадранте (см. рис. 44). Тогда площадь прямоугольника равна 4х₁х₂. Получилась такая формализация: найти наибольшее значение функции двух переменных

при условиях

Заметим теперь, что неравенства x₁ ≥ 0 и х₂ ≥ 0 можно отбросить. Вы легко сообразите, что задача о нахождении наибольшего значения функции

при условии

также является формализацией планиметрической задачи Кеплера.

Но теперь из уравнения f₁(х₁, х₂) = х²₁ + х₂₂ - 1 = 0 можно выразить х₂ через x₁ и подставить в выражение для f₀. Тогда (если x₁ обозначить через х) получится еще одна формализация: найти наибольшее значение функции φ(х) = 4x√(1 - х²) при условии 0 ≤ х ≤ 1 или при условии |х| ≤ 1 (это условие накладывается областью определения функции и смыслом переменной х).

Мы видим, что одну и ту же задачу можно формализовать по-разному. От того, насколько удачно формализована задача, часто зависит и успех ее решения. Формализация - это искусство. Ему нужно учиться, лучше всего - решая практические задачи.

Задача Кеплера, о которой мы здесь говорили,- планиметрическая. В пространстве можно поставить подобные задачи по-разному. Одна из постановок была обсуждена нами в первой части (вписать в единичный шар цилиндр наибольшего объема). Но возможна и другая постановка: вписать в единичный шар прямоугольный параллелепипед наибольшего объема. Эта постановка приводит к такой формализации: найти наибольшее значение функции трех переменных

при условии, что

(Частный случай этой задачи, когда x₁ = х₂, рассматривал, как мы помним, Кеплер.)

К той же формализации (правда, без восьмерки) приводит такая задача: найти наибольшее значение произведения трех чисел при условии, что сумма квадратов их равна заданному числу. Но теперь возможно и дальнейшее обобщение: вместо трех чисел можно взять и пять, и десять, и вообще любое количество. Формализация этой задачи будет такова: найти наибольшее значение функции n переменных

при условии, что

Теперь попытаемся уже достаточно определенно описать все элементы точно формализованной экстремальной задачи. Там обязательно должна присутствовать некоторая функция (скажем, n переменных), наибольшее или наименьшее значение которой надо найти (максимизируемая или минимизируемая функция).

Далее в формализованной задаче должно быть ограничение, задаваемое некоторым числом равенств или неравенств с теми же неизвестными.

Приведем несколько минимизируемых или максимизируемых функций и функций, задающих ограничения, из тех, что уже встретились нам или встретятся далее.

f₁, f₂, f₃ - функции одного переменного, g₁, g₂ - двух, h₁, h₂ - трех, F₀, F₁ - n переменных.

Таким образом, формализовать экстремальную задачу - это значит точно описать минимизируемую и максимизируемую функцию (обозначим ее f₀) и ограничение (обозначим его С). Ограничение задается обычно равенствами и неравенствами.

Для формализованной задачи: "найти минимум (максимум) функции f₀(x) при условии, что x из С" будем употреблять сокращенную запись^*

(з) f₁(х) → min (max) по х из С.

Точки из С называются допустимыми; если ограничений нет, то (з) называют задачей без ограничений.

Например, для одной из формализаций планиметрической задачи Кеплера сокращенная запись примет вид

(з₁) f(x₁, x₂) = 4x₁x₂ → max, f₁ (х₁, х₂) = х²₁ + х²₂ - 1 = 0,

а для задачи Герона будет просто

(з₂) f₀(x) = √(a² + х²) + √(b² + (d - х)²) → min.

Задача (з₁) - с ограничением типа равенств, (з₂) - задача без ограничений.

^* (Буквы з не следует бояться - это русская буква, первая буква в слове "задача". Для краткости набор переменных (x₁,..,x_n) обозначается буквой х. Далее мы говорим иногда "точка х". При этом если х = (x₁,...,x_n) и а, - число, то аx = (аx₁ ,..., аx_n), и если х' = (x'₁, ... , х'_n), то x + х' = (x₁ + x'₁, ..., х_n + х'_n).)

Допустимая точка х̂ называется абсолютным минимумом (максимумом) в задаче (з), если f(х) ≥ f(х̂) для любого х из С. (Соответственно f(х) ≤ f(х̂) для любого х из С.) Абсолютный минимум (максимум) задачи будем называть решением задачи. Найти решение и есть наша цель.

Но для того чтобы достичь ее, мы будем использовать методы нахождения так называемых локальных экстремумов.

Взобравшись на вершину холма или маленькой горки, расположенной на ровной местности, мы оказываемся в наивысшей точке этой местности. Но это не значит, что мы нашли решение задачи о самой высокой точке над уровнем моря. Эту последнюю задачу "решили" лишь те люди, которые побывали на Эвересте.

Такова разница между абсолютным и локальным экстремумами.

Дадим точное определение последнего понятия. Будем говорить, что точка х̂ = (х̂₁ ..., х̂_n) доставляет локальный минимум (максимум) для задачи (з), если можно указать такое число ε > 0, что для всех точек х = (х₁ ,..., х_n) из С, для которых

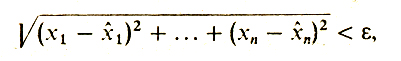
выполнено неравенство

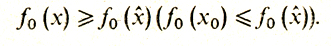
(Иначе говоря, если "вблизи" от точки х̂ значение функции в допустимой точке не больше (не меньше) f₀ (х̂).)

Прежде чем закончить этот рассказ, формализуем еще одну задачу, а именно транспортную, о которой мы мимоходом сказали в первом рассказе. Напомним, что в транспортной задаче нужно составить план перевозок для того, чтобы доставить некоторый продукт из баз в магазины и чтобы стоимость перевозок была минимальной. Обозначим через a_i количество единиц груза на i-й базе. При этом число баз пусть будет равно m. Потребность j-го магазина в единицах перевозимого груза пусть исчисляется величиной b_j, j = 1, ..., n. Наконец, через c_ij выразим стоимость перевозки единицы груза из i-й базы в j-й магазин. Составить план перевозок - это значит указать числа x_ij, 1 ≤ i ≤ m, 1 ≤ j ≤ n единиц груза, которые следует перевезти из i-й базы в j-й магазин. Таким образом, количество груза, вывозимого с i-й базы, будет равно x_i1 + ... + x_in, и это число не должно превосходить а_i (никакая база не может дать больше, чем у нее есть), а количество продукта, привозимого в j-й магазин, равно x_1j + ... + x_mj, и это число должно быть равно в точности потребности магазина, т. е. b_j. Таким образом, транспортная задача допускает следующую формализацию:

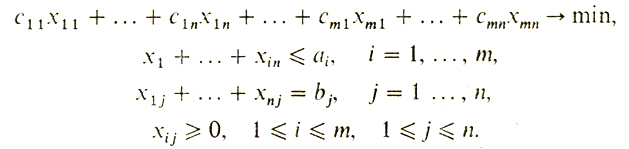
Обратим внимание на то, что и минимизируемая функция и ограничения в транспортной задаче задаются с помощью линейных функций. Раздел теории экстремальных задач, где изучают экстремумы линейных функций при линейных ограничениях, называется линейным программированием. К этому разделу относится и транспортная задача.

Следующий наш рассказ - об экстремумах функций одного переменного. Сейчас эту тему проходят в школе, но мы не побоимся некоторых повторений.