
Рассказ девятый. Что такое функция?
Это общее понятие требует, чтобы функцией от х называть число, которое дается для каждого х и вместе с х постепенно изменяется. Значение функции может быть дано аналитическим выражением, или условием, которое подает средства испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной.
Обширный вид теории допускает существование зависимости только в том смысле, чтобы числа, одно с другим в связи, принимать как бы данными вместе.
Прежде чем приступать к рассказам о методах исследования задач на максимум и минимум, поговорим о функциях.
Функция - основное понятие математического анализа. Но формировалось оно не сразу. Вначале оно было расплывчатым и не имело сколько-нибудь четкого описания. Первые попытки очертить контуры этого понятия делаются в конце XVII века Лейбницем, Иоганном и Якобом Бернулли. Сам термин "функция" принадлежит Лейбницу. И. Бернулли вкладывает в этот термин понятие о "выражении, составленном каким-либо образом из переменной величины и постоянных величин". Конкретизируя мысль И. Бернулли, Эйлер в своих учебниках определял функции как аналитические выражения, составленные из переменной величины и постоянных величин. Он же ввел символ f(х). Однако Эйлер считал возможным называть функцией также "произвольно начерченную кривую". Но Эйлеру были известны также и такие случаи, когда Функция имела словесное описание. Скажем, тот же синус.
Рассмотрим один простой пример функции, допускающей разные описания. Это y = |х|. Несомненно, что |х| = √х2 = (x2)1/2 есть (аналитическое) выражение, составленное из переменной величины х и постоянных величин. Так что это - функция и по И. Бернулли, и по Эйлеру. Но ее же можно изобразить и как "начерченную кривую", идущую по биссектрисам первого и второго квадранта в декартовой системе координат. Ее же можно описать и словесно, сказав, что для х, равного нулю, эта функция равна нулю, для положительного х она равна самому х, для отрицательного х она равна - х. И вообще большинство функций допускают разные описания.
Чему же отдать предпочтение? По этому поводу было много споров. Скажем, Эйлер считал, что класс функций, являющихся "произвольно начерченными кривыми", шире, чем класс функций, задаваемых "аналитическими выражениями". Даламбер возражал ему, он утверждал, что получится одно и то же.
Д. Бернулли выдвинул, казалось бы, совсем парадоксальную точку зрения на функцию: он высказывал убеждение, что произвольную периодическую функцию с периодом 2π можно представить в виде суммы
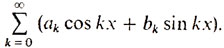
Большинству же казалось, что это - лишь некоторый узкий класс функций, что он уже, чем "аналитические выражения" и, разумеется, чем "произвольные кривые".
В начале прошлого века стала выкристаллизовываться идея функции, как соответствия, закона, по которому независимое переменное х преобразуется в y, вне зависимости от способа такого соответствия. Среди первых ученых, пропагандировавших такую точку зрения, был Лобачевский. Его слова по этому поводу были вынесены нами в эпиграф к нашему рассказу.
Сходные воззрения и примерно в те же времена высказывались и во французской математической школе и в немецкой. В начале века в учебниках по математическому анализу стали приводиться такие, например, определения функции.
"Пусть даны две переменные х и у, между значениями которых существует какая-нибудь зависимость. Вообще, одну из переменных, например х, рассматривают, как независимую. Значение х может быть взято по произволу, но при данном х значение у не произвольно. Говорят тогда, что у есть функция от х" (Валле-Пуссен). Или: "Переменная величина у называется функцией от переменной величины х, если каждому значению х соответствует одно определенное значение y" (Немыцкий, Слудская, Черкасов).
Однако людей, особо приверженных к логической строгости (вообще говоря, таких людей не так уж много), подобные определения удовлетворить не могут. Ведь в них термин "функция" определяется через понятия, которые столь же неопределенны и столь же расплывчаты ("зависимость", "закон", "соответствие" и т. п.).
Некоторое успокоение пришло с созданием теории множеств, начала которой были заложены в конце прошлого века Георгом Кантором. Там вроде бы все стало на свои места. Пусть X и Y-два множества. Множество F пар (х, у), х∈Х, y∈Y называется функцией, если для любого х ∈ Х существует единственное y такое, что (х, y)∈F. Тогда пишут y = f(х)*. Концепции теории множеств произвели огромное впечатление на многих математиков, которые были свидетелями зарождения новой теории. Гильберту, одному из величайших математиков всех времен, принадлежат следующие слова о теории множеств: "Я считаю, что она представляет собой высочайшее проявление математического гения и одно из самых высоких достижений чисто духовной деятельности человека". Нужно добавить при этом, что практически все современные математические работы так или иначе используют основные понятия теории множеств и ее символику.
* (Что-то очень близкое по смыслу содержится в последней фразе цитаты из Лобачевского, приведенной нами в качестве эпиграфа.)
Но, увы, через какое-то время стали раздаваться критические голоса. Обнаружились противоречия, и снова возникли жаркие споры. В начале нашего века все крупнейшие математики (Пуанкаре, Гильберт, Адамар, Вейль, Брауэр и другие) приняли участие в обсуждении проблем, связанных с кризисом основ всей математики. Для некоторых математиков теоретикомножественные определения (и в частности, определение функции) были неприемлемо широки. Они высказывали убеждение в том, что функциональная зависимость, представляющая интерес с практической точки зрения, неизбежно должна быть "конструктивной". Это значит, что должно быть отчетливое правило (или, как теперь принято говорить, - алгоритм), которое по данному х позволяет отыскивать нужное у. В итоге возникли целые направления в математике, отрицавшие теорию множеств. Стала разрабатываться особая "конструктивная" математика, похожая и непохожая на уже ставшую привычной для всех математику, основанную на теории множеств.
Многие ученые очень тяжело переживали кризис, связанный с отрицанием частью математиков теоретико-множественных концепций. Давид Гильберт так писал об этом: "Никто не изгонит нас из рая, созданного для нас Кантором". Иные же горячо оспаривали эту точку зрения.
Однако пора вернуться к нашим проблемам: что же такое функция?
Какому воззрению отдать предпочтение? Где истина? Углубленное продумывание этих вопросов увело бы нас слишком далеко. Но необходимо сказать, что для "общеупотребительных" целей, для решения реальных задач, для физики и более широко - для приложений математики в естественных науках, в технике, экономике и т. п. годятся все достаточно определенные описания понятия функции.
Практически всюду в этой книге для наших основных целей достаточно будет тогр понимания, которое начало оформляться у самых истоков математического анализа. Поэтому мы будем трактовать понятие функции "по Бернулли" как "выражение, составленное каким-либо образом из переменной величины и постоянных величин".
Функции различаются по числу переменных. Сначала поговорим о функциях одного переменного, которое является действительным числом. Если мы будем говорить о функции y = f(x), мы всегда будем иметь в виду какое-то точное предписание, следуя которому из числа х получится число у. По типу такого: "возьмите число, возведите его в квадрат, прибавьте к этому квадрату единицу и извлеките квадратный корень".
Так описывается функция y = √(1 + х2) - это, конечно, "выражение, составленное из переменной величины и постоянных величин". (Скажем, кстати, что воззрения Бернулли во многом смыкаются с воззрениями современных "конструктивистов": надо лишь расплывчатый термин "выражение" заменить термином "алгоритм", которому можно придать совершенно точный смысл, а по сути дела, алгоритм - это точно сформулированное предписание о том, что надлежит сделать с числом х для получения y.)
Функции одного переменного можно изображать графиками. Для этого ось х направим, как обычно, горизонтально слева направо, ось y - вертикально снизу вверх. Пересечение осей обозначим буквой О. Выберем масштаб по оси х и y. Теперь, выбрав число х, отложим его на оси Ох, а затем на перпендикуляре, проведенном через полученную точку, отложим отрезок длины y = f(x). Так получается график функции y = f(x). В частности, графиком функции y = √(1 + х2) будет гипербола (см. рис. 40).
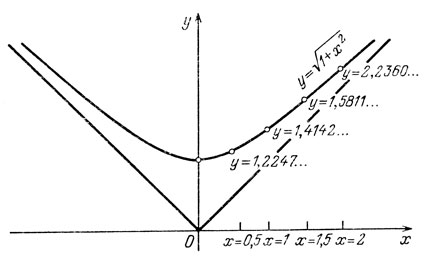
Рис. 40
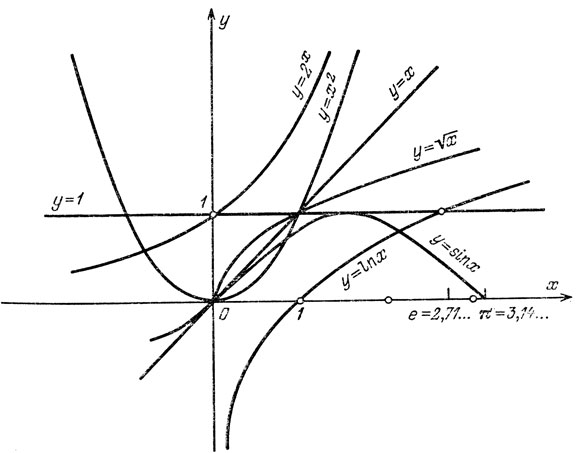
Рис. 41
А теперь давайте определим и затем изобразим несколько важнейших функций одного переменного.
Самая простая из функций - постоянная:
y ≡ с.
Каждому действительному числу х эта функция сопоставляет одно и то же число с. На рис. 41 изображена эта функция f(х) ≡ 1 при частном значении с, равном единице.
Следующие по сложности функции - линейные:
y = bх.
Здесь b - постоянное число, ах - любое действительное число.
Такие функции изображаются прямыми, проходящими через начало координат и не совпадающими с осью Оy. Пусть, скажем, b = 2. Тогда получится функция y = 2х. Если взять х = 1, то у окажется равным двум, если взять х = 0,25, то у будет 0,5 и т. д. - по каждому х совершенно определенным образом находится у, а именно х умножается на 2. На рис. 41 изображена самая простая из линейных функций - y = х. Ее график является биссектрисой угла, образованного осями Ох и Оy.
Из постоянной и линейной функций образуются функции вида
y = bх + с.
В школе именно такие функции называют линейными, но нам кажется, что их естественней называть аффинными. Аффинные функции в дальнейшем у нас будут играть важнейшую роль.
Затем идут квадратичные функции
y = ах2.
Такие функции изображаются параболами, проходящими через начало координат. Пусть, скажем, а = 0,5. Тогда если взять х = 1, то y = 0,5, если х = 2, то y = 2, если х = 10, то y = 50 и т. д., снова по каждому х совершенно определенным образом находится y, а именно х умножается на себя, а затем на 0,5. На нашем рисунке изображена функция
y = х2 (а = 1).
Из постоянной, линейной и квадратичной функций образуются квадратные трехчлены y = ах2 + bх + с.
Потом можно рассмотреть степенные функции
y = Ахn.
Здесь А - какое-то постоянное действительное, а n - целое число.
Важную роль в анализе играют показательные функции
y = ах.
Функция y = 2x изображена на рис. 41.
Очень употребительны функции, обратные к степенным и показательным. На нашем рисунке изображены функции y = √х и y = In х. Особенность этих функций в том, что они определены не для всех х. Функция y = √х определена только для неотрицательных х, а функция y = In х - только для положительных х (см. рис. 41).
Наконец, в школе проходят еще и тригонометрические функции. На рис. 41 изображена функция y = sin х.
Приведем список наиболее употребительных функций, с которыми постоянно придется иметь дело:
y = Аxn - степенная функция; при n = 0 - это постоянная функция, при n = 1 - линейная, при n = 2 - квадратичная;
y = √x - функция "корень n-й степени из х";
y = ах - показательная функция;
y = loga х - логарифмическая функция;
тригонометрические функции: y = sinх - синус, у = cosх - косинус, y = sin x /cos x = tg х - тангенс, у = cos x/sin x = ctg х - котангенс.
Из описанных функций можно составить разнообразные выражения, которые также все окажутся функциями одного переменного. Приведем примеры:
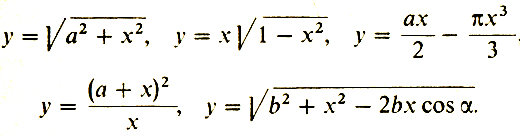
Конечно, этот список можно продолжить. Мы привели здесь лишь те функции, с которыми нам придется иметь дело, когда нужно будет решать экстремальные задачи. Но, разумеется, можно придумать и что-нибудь пострашнее, например,
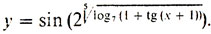
Здесь закодировано следующее предписание: взять число, прибавить к нему единицу, взять от суммы тангенс, ко всему прибавить единицу, из полученной суммы взять логарифм по основанию семь, далее следует извлечь из полученного числа корень пятой степени, возвести двойку в получившееся число и, наконец, найти синус этой степени двойки.
Такого рода "выражениями" ("предписаниями", "алгоритмами"), только чуть менее "страшными", в основном и будет исчерпано содержание понятия "функция одного переменного", с которым нам придется сталкиваться.
С функциями одного переменного вы встречались в школе. Поэтому выше о многом (и важном) было сказано вскользь, в расчете на то, что вы можете заглянуть в учебник, спросить учителя или додумать кое-что сами. Но функциями одного переменного нам дальше не обойтись. Нам необходимо будет "работать" с функциями двух, трех, четырех, ста переменных (и - пока по секрету - с функциями бесконечного числа переменных). Но не пугайтесь! Все это не так уж трудно.
Сначала сделаем лишь один шаг вперед и поговорим о функциях двух переменных.
Если спросить вас, когда впервые вы начали "работать" с функциями двух переменных, многие придут в недоумение. Функции двух переменных в школе не изучают - как же можно с ними "работать"? Но в действительности все мы знакомимся с функциями двух переменных с незапамятных времен. Именно - с незапамятных! Никто из вас и не вспомнит тот день, когда впервые ваш отец, или мать, или пришедший в гости знакомый задал вам вопрос вроде: "Вот яблоко, а вот еще,-сколько вместе?" Это было в самом раннем детстве, когда едва лишь освоена речь и еще далеко до знания букв. Тот момент, когда вы ответили на поставленный вопрос, вы не можете помнить. Но именно тогда, когда, прибавив к одному яблоку другое, вы получили "два" яблока, вы впервые столкнулись с функцией двух переменных, самой древней из них, самой известной - сложением.
Вот она:
z = x + y.
Если взять любую пару чисел х и y, то этой паре функция "сложение" сопоставит число z, равное сумме х и y. Паре (1, 1) будет сопоставлено число 2, паре (7, -3) - число 4 и т. д.
На первых порах вы осваивали сложение натуральных чисел, затем - целых; наконец, вас учили складывать любые числа. В итоге, любой паре (х, y), где х и y - действительные числа, вы сможете сопоставить их сумму, иначе говоря, операция "сложение" определена на любой паре (х, y), "где х и y - действительные числа.
Выходит, что с функциями двух переменных вы столкнулись гораздо раньше, чем с функциями одного переменного.
После сложения вас учили вычитать, умножать и делить. Вычитание, умножение и деление - все это функции двух переменных. Причем вычитание и умножение определены снова на любой паре (х, y), где х и y - действительные числа, а деление определено только на тех парах (х, y), для которых y ≠ 0.
И снова под функцией двух переменных мы будем понимать (вслед за Бернулли) выражение, составленное из переменных величин х и y и постоянных величин.
Функции двух переменных z = f(х, у) тоже можно изображать графически. Для этого изобразим плоскость хОу и проведем ось Oz перпендикулярно этой плоскости. Выберем масштаб на осях Ох, О y и Oz. Теперь, если нам заданы числа х и y, мы отложим их на плоскости хОу, затем вычислим значение f(х, y) и отложим на прямой, параллельной оси Oz и проходящей через точку (х, y), отрезок длины f(х, y).
Давайте теперь определим и изобразим несколько важнейших функций двух переменных.
И снова - самая простейшая функция - постоянная:
z ≡ с.
Каждой паре (х, y), где х и y - действительные числа, эта функция сопоставляет число с.
Следующие по сложности функции - линейные:
z = ах + by.
Здесь а и b - постоянные числа, а х и y - любые действительные числа. Для того чтобы получить z по паре (х, y), надлежит х умножить на а, у умножить на b и получившиеся z = х + y. Вообще же линейные функции изображаются плоскостями, проходящими через начало координат и не перпендикулярными плоскости хОy.
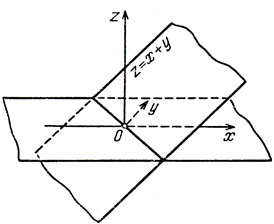
Рис. 42
Из постоянной и линейных функций образуются функции вида
z = ах + by + с,
которые мы также будем называть аффинными. Они далее будут играть для нас самую важную роль.
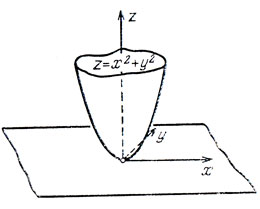
Рис. 43
Дальше идут квадратичные функции z = Ах2 + 2Вхy + Сy2 и функции вида
z = Ах2 + 2 Вхy + Сy2 + ах + by + с.
На рис. 43 изображена функция z = х2 + y2. Приведем еще несколько функций двух переменных, которые встретятся у нас далее при решении задач:
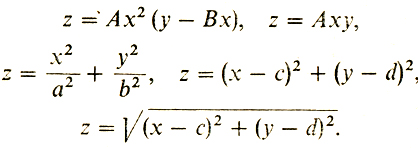
И еще несколько слов о функциях двух переменных. Одно обстоятельство позволяет нам наглядно представлять их характерные особенности, ибо график одной замечательной функции двух переменных всегда у нас перед глазами и "под ногами".
Вот вы стоите на земле. Ваше положение в пространстве можно задать тройкой чисел (φ, θ, h), где (φ, θ) - географические координаты - широта и долгота, a h - высота над уровнем моря. Таким образом, h = h(φ, θ), т. е. h есть функция (φ, θ). (Вспомним ту общую точку зрения на функцию, которую мы поставили эпиграфом к данному рассказу.) И все, что мы видим, - холмы, ложбины, овраги, горы, глади озер - все это есть "график" этой функции.
У нее имеется множество примечательных точек.
Прежде всего, конечно, это - вершины, поднявшись на которые, мы испытываем радость победы, восторг преодоления. Во время путешествия по горам мы ищем перевалы, чтобы из одной долины перейти в другую. Исследуя морское дно, мы стремимся отыскать самую глубокую точку моря. Этими же самыми точками - вершинами, перевалами, ложбинами - нам и надлежит заниматься дальше.
Расстанемся на время с функциями двух переменных и сделаем еще один шаг. Спросим себя: что такое функция трех переменных? Ну конечно же, это выражение, составленное из переменных х, y и z и постоянных величин.
Примеры? Сколько угодно! Сумма u = х + y + z, произведение u = х ⋅ y ⋅ z, постоянная функция u ≡ d, линейная функция u = ах + by + cz, квадратичная функция u = Ах2 + 2Вхy + Сy2 + 2Dyz + 2Gxz + Fz2, u = √(х2 + y2 + z2), u = 2х + log3 y + sin z и т. д. и т. п.
А что такое функция четырех переменных? Ну конечно же, - выражение, составленное из переменных х, y, z и постоянных величин.
А что такое функция двадцати шести переменных? Это, конечно, - выражение, составленное из переменных а, b, с, d, e, f, h, i, j, m, n, o, р, q, r, s, t, u, v, w, х, y, z и постоянных величин.
А из двадцати семи? Это, конечно, - выражение, составленное из переменных... Но ведь букв не хватит! Неужели изучать лишь функции не более 26 переменных? Конечно, можно еще добавить греческий алфавит и еще какие-то другие алфавиты. Но и всего этого будет мало. В современных экономических задачах - тысячи переменных! Что же делать?
Выход очень прост. Переменные можно обозначать не разными буквами, а одной буквой х, но с индексами: x1, x2 ..., xn. Постоянные же можно обозначить буквами начала латинского алфавита, и снова с разными индексами.
Таким образом, функции n переменных - это выражение, составленное из переменных x1, x2,...,xn и постоянных величин.
Простейшая функция n переменных - постоянная: y = с. Каждому набору из n чисел (x1,...,xn) она сопоставляет единственное число с.
Важнейший класс образуют линейные функции
y = а1х1 + ... + аnxn.
Из постоянных и линейных функций образуются функции вида
y = a1x1 + .... + аnxn + с.
Их называют аффинными.
Такого рода функциями мы будем аппроксимировать более сложные функции.
И теперь уже, быть может, настало время назвать вещи своими именами: мы с вами уже много раз сталкивались с функциями многих переменных. Это было, например, в пятом рассказе, когда речь шла о средних. Мы рассматривали там функции
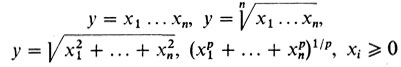
и т. д. Функции многих переменных встречались и в рассказе о брахистохроне
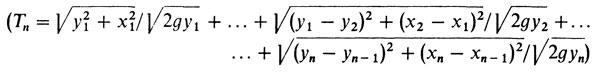
и в рассказе о задаче Ньютона. И там уже возникли функции еще более поразительные - "функции от функции", например от линии, т. е. в конечном счете - функции бесконечного числа переменных.
Наша цель в этой части книги - дать фрагмент общей теории экстремальных задач. Пока что мы объяснили, что такое функции многих переменных. В следующем рассказе мы объясним, как ставятся задачи на максимум и минимум функций многих переменных с ограничениями.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'