Рассказ седьмой. Брахистохрона

Если начальная и конечная точки движения одинаковы, то поскольку прямая есть кратчайшее расстояние между ними, то можно было бы думать, что движение, совершающееся по ней, требует наименьшего времени. На самом деле это не так.

Г. Галилей

Невозможно отрицать глубокое значение, какое имеют точно поставленные проблемы для продвижения математической науки.

Д. Гильберт

С 1682 года стал выходить в свет первый научный журнал - "Акта Эрудиторум". В июньском номере этого журнала за 1696 год была помещена заметка знаменитого швейцарского ученого Иоганна Бернулли с интригующим заглавием: "Новая задача, к решению которой приглашаются математики".

Часто случается, что постановка новой проблемы привлекает внимание многих выдающихся ученых. Соревнуясь друг с другом, они создают мощные методы решения задач, которые потом щедро служат науке. Так вышло и с задачей И. Бернулли. Вот как формулирует ее сам автор.

В вертикальной плоскости даны точки A и В (рис. 29). Определить путь АМВ, спускаясь по которому под действием собственной тяжести, тело М, начав двигаться из точки А, достигнет точки В в кратчайшее время.

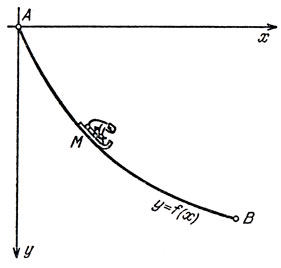
Рис. 29

Ставя свою задачу, И. Бернулли не упоминает Галилея. И напрасно! Все современное естествознание "вышло" из Галилея. И дело не только в том, что он открыл основополагающие законы механики. Величайшая заслуга Галилея перед человечеством в том, что он первым стал спрашивать у Природы. Нынешний этап развития науки начался в тот момент, когда Галилей поднялся на пизанскую башню для того, чтобы спросить у Природы

о ее законах падения тел.

Галилей проводил эксперименты с наклонными плоскостями. По-видимому, он ставил также опыты и на круговых желобах. Вот что пишет он в "Беседах о механике" - главном труде всей своей жизни: "Тела, опускающиеся по дугам, соответствующим хордам, наклоненным к горизонту..., совершают движение, как показывает опыт, также в равные промежутки времени и притом меньшие, нежели движение по хордам". Из двух утверждений Галилея относительно движения по дугам верно лишь одно: движение по дуге быстрее, чем по хорде. Второе же утверждение - относительно равенства промежутков времени - верно лишь приближенно, и этот факт впоследствии теснейшим образом оказался связанным с задачей И. Бернулли.

Но так или иначе и приведенные выше слова Галилея, и его слова, взятые нами в качестве эпиграфа, сразу наталкивают на вопрос И. Бернулли: какая же кривая соответствует кратчайшему времени движения, т е. какая же кривая является брахистохроной (по-гречески - наибыстрейшей)? Многие авторы упрекают Галилея в ошибке, утверждая, что он считал брахистохроной дугу окружности. В "Беседах" Галилей несколько раз возвращается к теме о сравнении движения по окружности и хорде, но ни в одном месте его слова нельзя истолковать так, что движение по дуге окружности - самое короткое среди всех кривых, соединяющих две заданные точки. Впрочем, может быть, какие-то его слова ускользнули от нашего внимания.

Однако пришло уже время вернуться к предмету нашего рассказа. Многие математики откликнулись на "приглашение" И. Бернулли. Одним из первых, решивших задачу о брахистохроне, был Лейбниц. Проблема ему очень понравилась, и он назвал ее прекрасной. Затем сообщили о своих успехах Якоб Бернулли (брат Иоганна) и Лопиталь. Сам Иоганн Бернулли, разумеется, располагал своим решением. Все эти ученые внесли значительный вклад в зарождавшееся новое направление - математический анализ. Но, кроме названных, было опубликовано и еще одно безымянное решение, в котором знатоки ex unge leonem ("как по когтям узнают льва" - эту латинскую поговорку процитировал И. Бернулли) сразу же узнали Ньютона. Ньютон потом признался, что потратил на решение этой задачи около 12 часов непрерывного обдумывания.

Все авторы пришли к одному и тому же выводу: брахистохроной является циклоида. Здесь уместно будет сказать похвальное слово этой замечательной кривой.

Циклоиду описывает точка окружности, катящаяся без скольжения по прямой. Напишем ее уравнение.

Пусть l - горизонтальная прямая, по которой катится окружность радиуса R, имеющая центром точку О. Допустим, что в нулевой момент времени точка окружности, за которой надлежит следить, расположена в точке касания окружности с прямой l. Обозначим эту точку через А₀. Пусть в этот начальный момент времени А₀ совпадает с началом координат, где ось x направлена по прямой l, а ось y - в перпендикулярном направлении (рис. 30). Посмотрим, где окажется точка А₀ после того, как окружность повернется на угол φ по часовой стрелке. Для этого отложим точку А_φ на первоначальной окружности так, чтобы угол А_φOA₀ был равен φ. Когда окружность при своем движении повернется на угол φ, точка A_φ, займет положение точки касания. Таким образом, абсцисса центра нового положения окружности будет равна R_φ, ибо такова длина дуги от А₀ до A_φ. При этом наша точка А₀ займет такое положение, что угол А₀ОА_φ будет равен φ. Отсюда следует, что координатами (х(φ), y(φ)) точки А₀ будут числа

Вот мы и получили уравнение циклоиды, которая при φ = 0 проходит через начало координат. В общем случае появляется еще один параметр

Что же такого примечательного в этой кривой? Как она возникла?

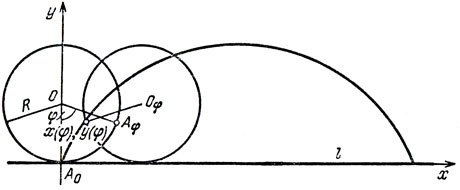
Рис. 30

Циклоида впервые появилась в работах Галилея, для иллюстративных целей. Он же дал ей название циклоида, т. е. связанная с кругом". Вскоре эту кривую переоткрыли во Франции (Мерсенн, Роберваль, Декарт, Ферма, Паскаль) и назвали рулеттой или трохоидой. Первое чудо, случившееся с этой кривой, состоит в том, что она служила как бы полигоном, на котором проверялись новые виды оружия, впоследствии поступившего в арсенал математического анализа.

Античная математика оставила будущим поколениям совсем мало кривых. Главные кривые античности - окружность, а также эллипс, гипербола и парабола, появившиеся у Аполлония. И все. Счастье, что первые законы механики не вывели за пределы этого запаса кривых: планеты движутся по эллипсам, а брошенные тела летят по параболам.

Так вот, долгое время все крупнейшие математики XVII века (кроме названных, еще Вивиани, Торричелли и некоторые другие) оттачивали свои новые методы исследования именно на циклоиде: проводили касательные, находили площади под ней, вычисляли длину ее дуг и т. д.

А затем случилось второе чудо. Циклоида стала первой "неантичной" кривой, которая оказалась связанной с законами природы. Выяснилось, что именно циклоида, а не окружность, как писал Галилей, обладает тем свойством, что тело, скользящее по ней без трения, совершает колебания периода, не зависящего от начального положения. Это свойство циклоиды - ее таутохронность (т. е. равновременность) - открыл Гюйгенс. Его работа произвела подлинную сенсацию. Сам Гюйгенс писал об этом: "Наиболее желательным плодом, как бы величайшей вершиной этого учения Галилея о падении тел, является открытое мною свойство циклоиды".

И вот вновь циклоида появилась по совершенно другому поводу...

Теперь уже пора переходить к решению задачи. Мы помним, что имелись пять решений; И. Бернулли, Лейбница, Я. Бернулли, Лопиталя и Ньютона. Все они были очень содержательны. Лейбниц применил прием, который далее развил Эйлер (суть его можно понять из письма Лейбница к И. Бернулли, приводимого нам далее). Ныне метод Лейбница - Эйлера является одним из основных методов решения задач на максимум и минимум - это так называемый прямой метод в вариационном исчислении. Я. Бернулли основывал свое решение на принципе Гюйгенса и сделал, таким образом, еще один шаг к созданию теории Гамильтона - Якоби (о ней было кратко упомянуто в третьем рассказе). Но наибольшую популярность получило решение самого автора. Не счесть книг, где оно приведено. Приведем его и мы.

Введем в плоскости систему координат (х, y) так, чтобы ось х была горизонтальна, а ось y - направлена вниз. При этом поместим точку А в начало координат (рис. 29). Пусть уравнение кривой (желоба), соединяющей точку А с точкой В, координаты которой равны (а, b) будет задано функцией y = f(х). Сначала нам надлежит вычислить время,, за которое тело М массы m (без трения) спустится из точки А в точку В по желобу f(x). Из механики известен закон Галилея, согласно которому скорость тела в точке с координатами (х, f(х)) (при движении под действием тяжести без трения) не зависит от формы кривой f между точками А и (х, f(х)), а зависит лишь от ординаты f(х). "Скорости падающих весомых тел находятся между собою в отношении корней квадратных из пройденных высот",- пишет И. Бернулли.

Действительно, кинетическая энергия нашего тела в точке (х, f(х)) равна mυ²/2 и эта энергия равна разности потенциальных энергий, т. е. mgf(х). В итоге, скорость в точке (х, f(х)) оказывается равной √(2gf(x)) (где g - ускорение силы тяжести). Рассмотрим теперь участок пути между точками (х, f (х)) и (х + dx, f (х + dx)), где dx - малое приращение абсциссы. Длина ds этого участка пути примерно равна √(dx² + (f(х + dx) - f(х))²). Воспользовавшись приближенным равенством f(х + dx) - f(х) ≈ f'(х) dx, получаем, что ds = √(1 + (f'(х))²) dx. Скорость движения на малом участке можно считать постоянной и равной √(2gf(x)). В итоге время dt, требующееся для прохождения нашего малого участка, окажется примерно равным

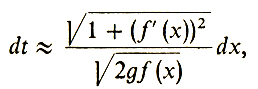
а все время Т движения от А до В запишется в виде интеграла

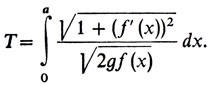
Таким образом, получается следующая аналитическая форма для задачи о брахистохроне. Требуется найти минимум интеграла

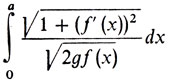
по всем функциям f, для которых f(0) = 0, f(a) = b.

Мы записали нашу задачу на языке математики, в данном случае на языке интегрального исчисления. Эта процедура называется формализацией задачи. (Подробнее об этом будет сказано в десятом рассказе.) Элементы интегрального исчисления проходят теперь в школе, но в самом конце, в десятом классе, а эта книга адресована более широкому кругу школьников, не только тем, кто заканчивает десятый класс. Поэтому объясним происходящее без ссылки на интегральное исчисление. Сделаем это в духе рассуждений математиков XVII века. Напомним при этом, что основные понятия анализа возникли всего за 12 лет до статьи И. Бернулли, и период "строгости" был еще далеко впереди.

Разделим отрезок [0, b] оси ординат на n частей точками 0 = y₀; y₁, y₂,...,y_n = b и найдем те абсциссы x_i, для которых f(x₁) = y₁ и f(х₂) = y₂, ,...., f(х_n-1) = y_n-1, x_n = а. Точки (х_i, y_i) и (x_i+1, y_i+1) где i = 0, 1, ...., n - 1, соединим отрезками прямых.

Тогда наряду с функцией y = f(х) возникает ломаная L_n, соединяющая те же точки А и В (рис. 31). Эта ломаная "аппроксимирует" (т. е. приближает) функцию y = f(х), и тем точнее, чем больше n. И время скольжения тела М по этой ломаной будет близко ко времени скольжения тела М по желобу, задаваемому функцией y = f(х).

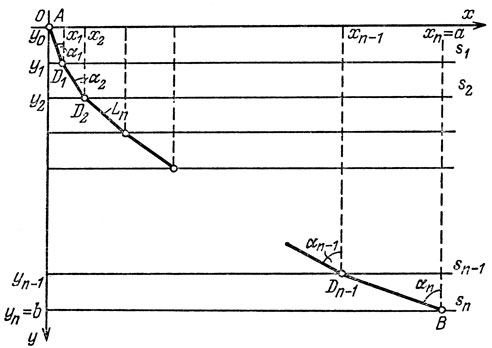
Рис. 31

Скорость движения по i-му отрезку ломаной можно приближенно считать постоянной и равной √(2gy_i+1), i = 0, 1,..., n = 1. При этом допущении время Т_n движения по n-звенной ломаной можно вычислить точно:

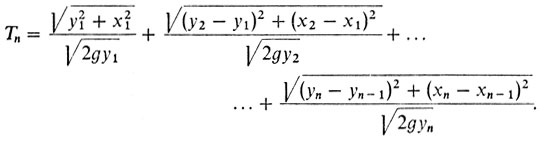(2_n)

Это время требуется минимизировать.

Предел Т_n при n → ∞ и будет искомым временем движения тела М по кривой y = f(х). Этот предел и есть тот интеграл (2) , который был выписан выше. Но мы, следуя И. Бернулли, будем решать не задачу, сформулированную выше с помощью интегрального исчисления, а именно соответствующую (2") приближенную "дискретную" задачу. Приведем ее формулировку.

Даны две точки A и В, координаты которых (0, 0) и (а, b). Требуется на прямых l₁,...,l_n параллельных осям абсцисс и имеющих ординаты y₁, ..., y_n, найти точки D₁ = (x₁, y₁), ... ..., D_n-1 = (x_n-1, y_n-1) так, чтобы сумма Т_n была минимальна (считая, что х₀ = y₀ = 0, х_n = а, y_n = b).

К этой задаче И. Бернулли применил замечательный прием, который оказал сильное влияние на всю последующую историю естествознания. О нем мы сейчас и расскажем.

Оптико-механическая аналогия. Вернемся немного назад, к третьему рассказу. Там мы поставили и решили задачу о преломлении света. Давайте внимательно вникнем в ее содержание и сравним его с задачей (2_n), где n = 2. В обоих случаях даны две точки и горизонтальная прямая, и требуется найти точку на этой прямой так, чтобы минимизировать "взвешенную" сумму длин. Только в третьем рассказе скорости были произвольны - υ₁ и υ₂, и мы, по сути дела, минимизировали функцию

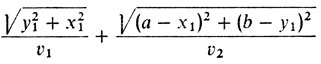(3)

(если координаты точки А = (0, 0), точки В = (а, b), а уравнение прямой l таково: y = y₁), а здесь имеется частный случай - мы должны минимизировать функцию

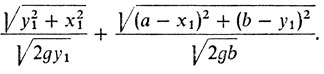(3')

К этому же выводу пришел и Г. Лейбниц, а далее он пошел своим путем. Свой метод Лейбниц прекрасно выразил в письме к И. Бернулли (от 31 июня 1696 г.). Он пишет: "Мой метод несколько отличен от твоего, но однако, приводит к тому же; для того чтобы, как требует справедливость, ответить на твою откровенность тем же, то вот он в немногих словах: заменив кривую многоугольником с бесконечно большим числом сторон, я вижу, что из всех возможных случаев (кривой) быстрейшего ската будет, если взять на ломаной три какие-нибудь точки, или вершины А, С и В, причем точка С будет такой, что из всех точек, расположенных на горизонтальной кривой l, эта единственная дает скорейший путь от А к В. Таким образом, дело сводится к решению легкой задачи: даны две точки А и В и проходящая между ними горизонтальная прямая l; найти на этой прямой точку С, чтобы путь АС В был наискорейшим". (Мы несколько изменили обозначения Лейбница, чтобы подогнать их к своим: у него вместо С - В, вместо В - С, вместо l - прямая DE.)

И. Бернулли поступил по-другому. Представим себе неоднородную оптическую среду, состоящую из n однородных слоев s₁, ..., s_n (посмотрим снова на рис. 31). Это можно представить себе, как n стекольных пластов, состоящих из разных стекол. Пусть при этом скорость распространения света в слое s 1 равна √(2gy₁), в слое s₂ - √(2gy₂),а в слое s_n - √(2gy_n). Каково же будет время распространения света, если его заставить идти по ломаной L". Очевидно, что Т_n, где Т_n задано формулой (2").

Таким образом, свет, согласно принципу Ферма, о котором говорилось в третьем рассказе, "решает" именно задачу (2n) (если условиться, что скорость распространения света в i-м слое равна

Отталкиваясь от механической задачи, мы вместе с И. Бернулли пришли к задаче оптической. Здесь впервые сработала оптико-механическая аналогия, которая затем принесла столько открытий в трудах Гамильтона, Якоби, Де Бройля и многих других.

Теперь уже можно перейти к решению И. Бернулли задачи о брахистохроне. Применим к задаче (2") в ее оптическом варианте закон Снеллиуса (о нем говорилось в третьем рассказе). Обозначим через α_i угол падения луча в i-м слое. В силу закона Снеллиуса получаем

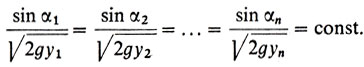(4)

Переходя к пределу при измельчении слоев, получим

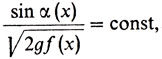(5)

где α(х) - угол между касательной к кривой y = f(х) в точке (х, f(х)) и осью Оy. Как известно, угловой коэффициент (т. е. тангенс угла, образованного касательной к графику функции f в точке х с осью Ох) равен f' (х). Отсюда сразу следует, что f' (х) = tg ((π/2) - α(х)) = cos α(x)/sin α(х), и значит,

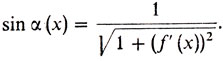
Из последнего равенства и (5) вытекает, что функция, график которой является решением задачи о брахистохроне, удовлетворяет соотношению

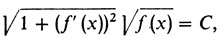
где С - некоторая константа. Иначе говоря, функция должна удовлетворять дифференциальному уравнению

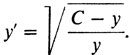(6)

А во времена И. Бернулли уже было известно, что уравнение (6) есть дифференциальное уравнение циклоиды.

Для тех, кто овладел некоторыми навыками интегрирования, произведем интегрирование уравнения (6).

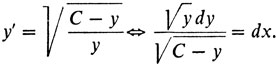
Делаем подстановку y = С sin² (t/2) = С(1 - cos t)/2. Тогда

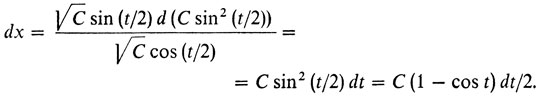
Интегрируя последнее соотношение, получим

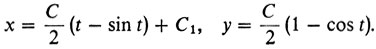(7)

Но это и есть уравнение циклоиды (1), следует лишь произвести замены букв: С/2 → R, t → φ.

Из полученных формул немедленно вытекает простой рецепт построения искомой циклоиды, т. е. той циклоиды, которая является решением задачи И. Бернулли. Отметим, что, во-первых, все циклоиды (7) гомотетичны, а во-вторых, выпуклы. Следовательно, можно взять любую из них, имеющую точку А = (0,0) своей левой вершиной (рис. 32), соединить точку (0, 0) с точкой В прямой, которая пересечет построенную циклоиду в точке В' и затем следует сделать гомотетию с коэффициентом |АВ'|/|АВ|. Так получается искомая брахистохрона.

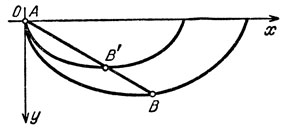
Рис. 32

Решение задачи о брахистохроне доставило ее автору необыкновенную радость перво-открывательства. Вот как он говорит об этом: "Я не могу воздержаться от того, чтобы еще раз не выразить своего изумления по поводу отмеченного неожиданного тождества между гюйгенсовской таутохроной и нашей брахистохроной... Природа всегда действует простейшим образом, - так и в данном случае она с помощью одной и той же линии оказывает две различных услуги".

Метод Иоганна Бернулли дал возможность решить еще несколько замечательных задач из оптики, механики и геометрии. Приведем две такие задачи.

Задача 1. Какова траектория световых лучей в атмосфере, где скорость распространения пропорциональна высоте?

Этим вопросом задался Лопиталь, автор первого в истории учебника по математическому анализу. (Правда, недавно выяснилось, что в основной своей части этот учебник представляет собой обработку лекций, которые читал Лопиталю все тот же И. Бернулли.) Лопиталь сумел проинтегрировать уравнение и, таким образом, ответить на поставленный вопрос. А по прошествии примерно двухсот лет выяснилось, что его решение имеет прямое отношение к геометрии Лобачевского: траектории световых лучей такие же, как прямые Лобачевского в интерпретации Пуанкаре.

Задача 2. Найти минимальную поверхность вращения.

Здесь надо сказать несколько слов, чтобы смысл задачи стал вполне ясен. Рассмотрим функцию y = f(х), соединяющую две точки плоскости (х₀, y₀) и (х₁, y₁) и неотрицательную. Совершим ее обращение вокруг оси Ох. Получим поверхность вращения. Ее площадь задается формулой

В задаче 2 требуется найти формулу кривой y = f (х), при которой эта площадь минимальна.

Задачу о минимальной поверхности вращения решили И. Бернулли и Лейбниц. Попробуйте и вы решить ее и задачу Лопиталя самостоятельно. А мы вместе обсудим их в четырнадцатом рассказе.

Задаче о брахистохроне суждено было сыграть выдающуюся роль в математическом анализе: она оказалась первой в ряду задач, из которых сформировалось вариационное исчисление.

Правда, незадолго до брахистохроны Ньютон рассматривал нечто похожее. Но об этом - в следующем рассказе.