Рассказ восьмой. Аэродинамическая задача Ньютона

Эта книга ("Начала натуральной философии" Ньютона) навсегда останется памятником глубины гения.

П. Лаплас

Ошибаются ли гении? Обычно, если задают такой вопрос, то предполагают утвердительный ответ на него. Есть нечто утешительное в сознании, что и гениям свойственно заблуждаться. Об ошибках гениев пишут с большим воодушевлением. Доставалось и Ньютону. В одной из книг, посвященных задачам оптимизации, написано так: "Ньютон сформулировал вариационную задачу о теле вращения, испытывающем наименьшее сопротивление в газе. Принятый им закон сопротивления физически абсурден, в результате чего поставленная им задача не имеет решения (чем более зазубрен профиль, тем меньше сопротивление)... Если бы выводы Ньютона были хотя бы приблизительно верны, то мы не нуждались бы сегодня в дорогостоящих экспериментах в аэродинамических трубах".

Что же это за задача и насколько справедливы приведенные выше критические слова? Об этом и пойдет речь в этом рассказе.

В 1687 году вышли "Математические начала натуральной философии" Ньютона. Никакое произведение научной литературы не может быть сопоставлено с этой книгой. В ней Ньютону было суждено открыть систему мира, а такое может случиться лишь однажды. Лагранж назвал это сочинение "величайшим из произведений человеческого ума"; "памятником глубины гения", назвал "Начала" Лаплас.

В этой книге, помимо открытия основных законов механики, законов движения планет и других основополагающих фактов, уделено место и многим частным проблемам.

Обсуждая вопросы, связанные с сопротивлением, оказываемым материальным телам средой, в которой они движутся, Ньютон как бы мимоходом бросил следующую фразу: "Когда же фигура DNFG будет кривою такого рода, что если из любой ее точки N опустить на ось перпендикуляр NM и из заданной точки G провести прямую GR, параллельную касательной к кривой в точке N и пересекающую ось у в точке R, то имеет место пропорция MN : GR = GR³ : (4BR ⋅ GB²), тогда тело, образующееся при обращении этой кривой около оси АВ, при движении в вышеупомянутой редкой среде в направлении от А к В будет испытывать меньшее сопротивление, нежели всякое иное тело вращения, описанное на той же длине и ширине" (рис. 33).

Фраза Ньютона привлекла к себе внимание современников лишь после того, как спустя девять лет, в 1696 году, И. Бернулли поставил свою задачу о брахистохроне, о которой речь шла в предыдущем рассказе.

В сиянии брахистохроны задача Ньютона заняла положение несчастной Золушки: ее как-то избегали, вспоминали о ней редко, да и то, как правило, чтобы поведать о заблуждении гения. На все это были свои причины. Но как и для Золушки, так и для задачи Ньютона пришел свой час.

Попробуем проникнуть в замысел Ньютона.

При конструировании кораблей, снарядов, торпед или ракет естественно возникает стремление придать им такую форму, чтобы они испытывали возможно меньшее сопротивление при своем движении. Ньютон пишет: "Можно сравнить сопротивление тел между собой и находить те, которые наиболее приспособлены к продолжению своего движения в сопротивляющейся среде". Но, если, скажем, корабль или самолет не может иметь слишком большой симметрии своего корпуса, то головки ракет, снарядов и торпед естественно делать круглыми в поперечном сечении; иными словами, им резонно придавать форму тел вращения. Но какую именно? Сферическую, коническую, веретенообразную или еще какую-нибудь? На такие вопросы нельзя ответить без вычислений, без решения некоторой математической задачи на максимум и минимум. Именно такую задачу ставит (и решает в приведенной выше фразе) Ньютон.

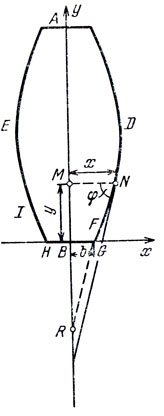
Рис. 33

В самом первом приближении задача ставится так.

Задача. Найти тело вращения заданной длины и заданной ширины, испытывающее наименьшее сопротивление при движении в некоторой среде.

Пояснения. Каждый из терминов, участвующий в формулировке (длина, ширина, движение и среда), требует точного описания.

Ньютон представляет себе тело вращения одинаковым сзади и спереди, т. е. симметричным относительно плоскости, проходящей через середину оси вращения и перпендикулярной этой оси. Таким образом, длина тела - это его длина по оси вращения, а радиус срединного сечения - это ширина тела. Из сказанного вытекает, что при всех рассмотрениях можно ограничиться лишь половинкой тела. Так мы дальше и поступаем.

Теперь - о движении. Будем считать, вслед за Ньютоном, что движение, совершаемое телом, - это равномерное движение с постоянной скоростью υ.

Наконец, о среде. Это наиболее тонкий и принципиальный вопрос. Среда, описанная Ньютоном, несколько необычна. Он сам называет ее "редкой" (разреженной). Ньютон представляет себе редкую среду "состоящей из равных частиц, свободно расположенных на равных друг от друга расстояниях". Неподвижные частицы имеют фиксированную массу m и являются абсолютно упругими шарами. Само тело Ньютон считает также абсолютно упругим, так что каждый шарик, столкнувшись с движущимся телом, отскакивает от него по закону "угол падения равен углу отражения".

После приведенных пояснений можно было бы сразу точно поставить и начать решать общую задачу, но мы поступим по-другому. Сначала исследуем более простой вопрос. С этого более простого вопроса, кстати говоря, начинает и сам Ньютон.

Задача об усеченном конусе. При данных основании и высоте усеченного конуса найти тот конус, который испытывает наименьшее сопротивление при движении в редкой среде.

Определим силу сопротивления, испытываемую усеченным конусом при движении в редкой среде.

Пусть усеченный конус имеет высоту, равную Я, и радиус верхнего основания R (рис. 34). Часть рис. 34, выполненная жирными линиями, содержится в "Математических началах".

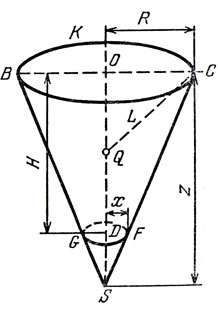
Рис. 34

Ньютон пишет: "Так как действие среды на тело то же самое... движется ли тело в покоящейся среде или же частицы среды ударяют с той же скоростью на покоящееся тело, то будем рассматривать тело в покое". Поступим так же и мы: оставив конус неподвижным, мы будем считать, что на него снизу вверх "надвигается" среда со скоростью υ.

Поверхность конуса, испытывающая столкновения с шариками среды, состоит из его нижнего основания и боковой поверхности. Сначала вычислим сопротивление, испытываемое нижним основанием. Обозначим его радиус через х. За единичное время с этим основанием столкнутся шарики, которые первоначально находились в цилиндре с основанием, равным нижнему основанию, и высотой, равной v. Объем этого цилиндра V₀ равен πx²υ. Пусть ρ - плотность среды, m - масса одной частицы. Тогда число частиц, ударившихся о нижнее основание за единичное время, будет равно N₀ = ρ/m V₀ = ρ/m πx²υ. Каждая частица после удара о нижнее основание сменит свою скорость на противоположную, т. е. получит приращение импульса, равное - 2mυ. По третьему закону Ньютона конус получит противоположное приращение импульса, и значит, общее приращение импульса от всех частиц будет равно N₀2mυ = 2πρx²υυ². Аналогично обстоит дело и для боковой поверхности. О нее ударяются частицы, помещаемые в объем между двумя одинаковыми боковыми поверхностями, и этот объем V₁ равен к π(R² - х²)υ. Число частиц, ударившихся о боковую поверхность, равно N₁ = ρ/mV₁ = ρ/m π(R² - x²)υ. Но здесь надо аккуратнее подсчитать приращение импульсов. Отразившись от стенки, частица получит приращение импульса m(υ₂ - υ₁) (рис. 35). Этот вектор надо спроектировать на ось y. Из рисунка легко понять, что эта проекция равна - 2mυ cos² φ, где φ - угол наклона образующей конуса к плоскости нижнего основания. Таким образом, общее приращение импульса от всех частиц, ударившихся о боковую поверхность, равно

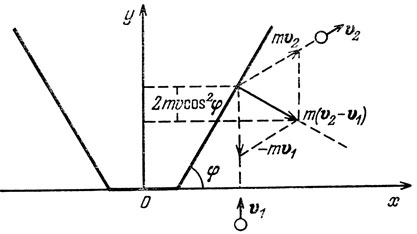
Рис. 35

Отметим (для будущего) формулу для силы сопротивления, испытываемого боковой поверхностью усеченного конуса, получающегося при вращении вокруг оси y отрезка [АВ] наклоненного к оси под углом φ, с абсциссами концов, равными а и b соответственно:

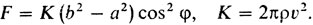(1)

В результате получаем следующее выражение для сопротивления, испытываемого всем конусом:

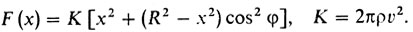
Выражение cos φ через х найти очень легко:

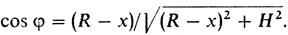
Постоянный множитель К не влияет на поведение максимальных и минимальных величин, и мы его отбросим.

Теперь можно формализовать задачу об усеченном конусе.

Задача 1.Найти минимум функции

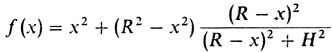(2)

при условии, что 0 ≤ x ≤ R

Перевод задачи на язык математики, как правило, не однозначен. И здесь, наряду с проведенной формализацией, можно предложить другое математическое описание той же задачи. Эта другая форма будет нам также очень полезна. Приведем ее.

Продолжим отрезок прямой, соединяющей точки С и F (рис. 34), до пересечения с осью y в точке S. Длину отрезка OS примем за новое переменное z. Из подобия треугольников SOC и SDF получаем: x/R = (z - H)/z, откуда R - х = RH/z и х = R (z - H)/z. Подставив эти выражения в (2), получим новое выражение для силы сопротивления (деленной на К) через новую переменную:

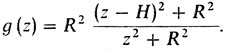(3)

При этом z изменяется от H до бесконечности. Таким образом, мы пришли к следующей формулировке задачи об усеченном конусе (постоянный множитель R² снова отбрасывается).

Задача 1.Найти минимум функции

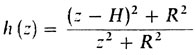
при условии, что z ≥ H.

Решим задачу 1'. Эта задача получилась столь простой, что решить ее можно даже и без помощи дифференциального исчисления. При этом мы получим ответ в той же форме, как и у Ньютона.

Обозначим наименьшее значение функции h через m. Таким образом, h (z) ≥ m для любого z ≥ H. При этом m ≤ h (H) = = R²/(R² + H²) < 1. Сделаем очевидные преобразования:

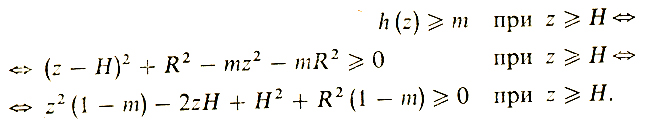
Если вдруг окажется, что существует такое m < 1, при котором неравенство (4) верно для всех z, и если при этом m можно найти ẑ ≥ H, которое обращает это неравенство в равенство, то это будет означать, что задача решена. Попробуем теперь отыскать нужные m и ẑ. Если имеет место неравенство az² + 2bz + с = 0 для всех z и при этом aẑ² + 2bẑ + с = 0, то отсюда следует, что D = b² - ас = 0 и ẑ = - b/а (продумайте это). У нас а = (1 - m), b = - H, с = H² + R² (1 - m). Уравнение D = 0 приводит к соотношению

откуда

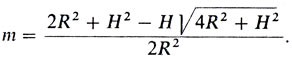
Знак " + " был отброшен, ибо то m, которое мы ищем, должно быть, как это было установлено, меньше 1. Далее,

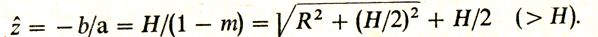(5)

В итоге нашлись такие m < 1 и ẑ > H, что дискриминант уравнения z² (1 - m) - 2zH + H² + R² (1 - m) = 0 равен нулю и оно имеет единственный корень ẑ ≥ H, т. е. h (z) ≥ m, h (ẑ) = m. Задача 1' решена.

Приведем ответ задачи об усеченном конусе в той форме, которую придал ему Ньютон: "Если на круговом основании СKВL(рис. 34), описанном из центра О радиусом ОС, требуется построить такой усеченный конус CBFG с высотою OD, коего сопротивление было бы меньше сопротивления всякого другого усеченного конуса, построенного на том же основании и высоте и движущегося по оси OD в сторону D, то разделив высоту OD в точке Q пополам, продолжи OQ до S так, чтобы было QS = QC, S и будет вершиною искомого конуса, который усекается".

Легко убедиться, что геометрическая форма, приданная ответу Ньютоном, в точности соответствует аналитической форме, заключенной в формуле (5).

Получилось, что конус наименьшего сопротивления на самом деле усеченный, затупленный, а не заостренный. Ньютон при этом идет еще дальше. Он устремляет высоту H к нулю. При этом ẑ устремляется к R и угол при основании конуса устремляется к 45°. Основываясь на этом, Ньютон делает замечение, что овальное тело следует заменять затупленным, т. е. делать спереди плоскую круглую площадку, образующую угол с примыкающей к площадке поверхности равный 135°. "Я считаю, что это замечание, - говорит Ньютон, - может быть не бесполезно при построении судов".

Задача Ньютона для двузвенной ломаной.

Сделаем еще один, предпоследний, шаг к решению общей задачи Ньютона. Будем рассматривать не любые кривые вращения, а лишь двузвенные ломаные с изломами на прямой х = R/2. То есть попробуем последовать методу Лейбница.

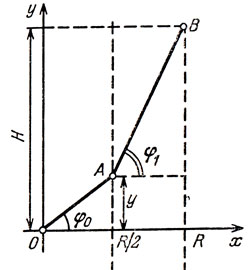
Рис. 36

Точнее говоря, вопрос, который мы собираемся исследовать, состоит в том, чтобы на вертикальной прямой х = R/2 найти такую точку А, чтобы поверхность, образованная вращением ломаной ОАВ (где В имеет координаты (Я, Я)) вокруг оси y (рис. 36) испытывала бы наименьшее возможное сопротивление в редкой среде Ньютона.

Пусть отрезок [ОА] наклонен к оси Ох под углом φ₀, а отрезок [АВ] - под углом φ₁. Обозначим

ординату точки А через у. Воспользовавшись формулой (1), получаем следующее выражение для силы сопротивления, испытываемого телом вращения двузвенной ломаной ОАВ:

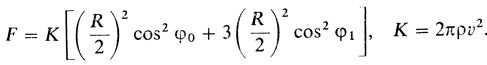
При этом

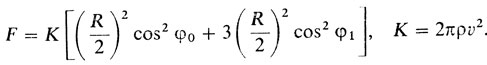
Таким образом, нам надлежит найти минимум функции

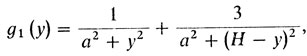
где мы снова сократили на множитель К и обозначили R/2 через a.

Однако очень легко сообразить, что при неограниченном возрастании |y| функция g₁ устремится к нулю. Вместе с тем она положительна. Значит, минимум этой функции равен нулю, хотя он и не достигается (подробнее аналогичный пример разбирается нами в одиннадцатом рассказе (п. 1)). Казалось бы, мы пришли к бессодержательной задаче... Но на самом деле из физических соображений вытекает, что нам надо найти минимум функции g₁ не по всем y, а лишь по у из отрезка [0, H]. Поясним это важное место.

Если взять y < 0, ломаная примет вид ОA'В, изображенный на рис. 37. Тело вращения, образованное этой ломаной, будет иметь коническую воронку, и значит, некоторые шарики, образующие редкую среду, будут многократно отражаться от поверхности этой воронки. При этом закон сопротивления будет совсем иным, причем сопротивление возрастет. Таким образом, из физической сути задачи следует, что нельзя допустить, чтобы y <0. Аналогично нельзя допустить, чтобы y был больше H. При постановке задачи неявно подразумевается монотонность кривой вращения. Так получается следующая формализация задачи о двузвенной ломаной.

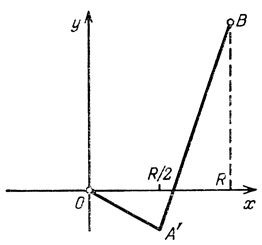
Рис. 37

Задача 2.Найти минимум функции

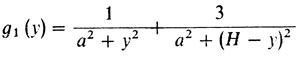
при условии, что 0 ≤ y ≤ H.

Решение задачи 2 нетрудно получить с помощью дифференциального исчисления.

Здесь мы ограничимся лишь формулировкой результата, который состоит в следующем:

а) существует такое δ > 0, что при 0 ≤ H ≤ δ минимум достигается в нуле;

б) для H > δ минимум достигается во внутренней точке отрезка [0, H]. При этом выполняется следующее равенство:

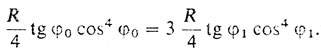
Таким образом, при достаточно малом Я тело вращения, образованное двузвенной ломаной, будет затупленным (усеченным конусом), при больших H - заостренным (его поверхность будет состоять из конической поверхности и боковой поверхности усеченного конуса).

Сделаем теперь последний промежуточный шаг.

Задача Ньютона для n-звенной ломаной и ее формализации. Рассмотрим совокупность вертикальных прямых l₁, l₂,..., имеющих уравнения

(рис. 38) и еще вертикальную прямую х = R (если R ≠ ^k/_n - для некоторого k). Рассмотрим совокупность всех монотонно возрастающих ломаных с изломами на прямых l_k, соединяющих точку (0, 0) с точкой (R, H). Попробуем среди всех описанных ломаных найти такую, чтобы поверхность, образованная вращением этой ломаной вокруг оси y, испытывала бы наименьшее сопротивление в редкой среде.

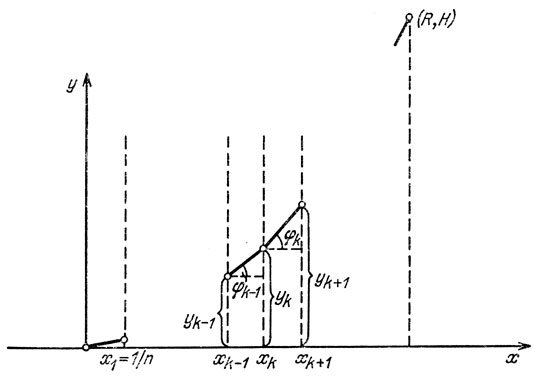
Рис. 38

Пусть ордината вершины ломаной, расположенной на прямой l_k, равна y_k угол наклона звена этой ломаной, соединяющей вершины, расположенные на l_k и l_k+1 с осью х обозначим через _k. Из формулы (1) получим следующее выражение для силы сопротивления, испытываемого телом, полученным от вращения нашей ломаной в редкой среде (для простоты считаем, что R = nN):

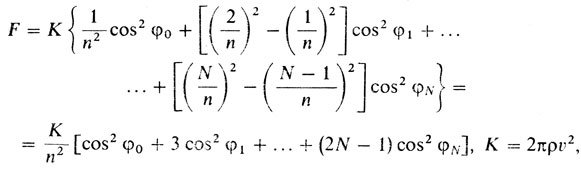
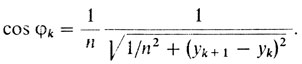(7)

Таким образом, задача Ньютона для N-звенной ломаной состоит в том, чтобы минимизировать силу F по всем возможным наборам чисел (y₁, ..., y_N) где 0 ≤ y₁ ≤ y₂ ≤ ... ≤ y_N-1 ≤ Н. Для решения этой задачи используем опыт, полученный при исследовании задачи 2, ибо по сути дела задача для N-звенной ломаной как бы распадается на N - 1 задачу типа задачи 2. Действительно, допустим, что нам удалось решить задачу об N-звенной ломаной и (ŷ₁ ..., ŷ_N-1) - ординаты вершин минимальной ломаной. Зафиксируем все вершины минимальной ломаной, кроме k-й вершины. При этом будем искать минимальное значение сопротивления, изменяя положение k-й вершины, иначе говоря, рассмотрим задачу типа задачи 2, когда требуется найти минимум функции

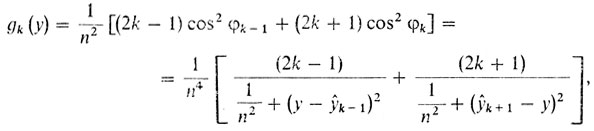
что при условии, что ŷ_k-1 ≤ y ≤ ŷ_k+1. Функция g_k составлена из двух слагаемых - (k - 1)-го и k-го, входящих в выражение для силы F (см. (7)), с учетом того, что ордината k-й вершины не закреплена и обозначена через y (множитель K мы, как обычно, опускаем). Решение поставленной задачи, очевидно, есть ŷ_k.

Задача о минимизации функции g_k подобна задаче 2, и для нее справедливы те же заключения, которые мы сделали для задачи 2. А именно:

а) существует такое число δ_k > 0, что при ŷ_k+1 - ŷ_k-1 ≤ δ_k минимум достигается при ŷ_k = ŷ_k-1;

б) для ŷ_k+1 - ŷ_k-1 > δ_k имеет место равенство

Из утверждений а), б) сразу вытекает, что экстремальная ломаная может иметь лишь следующий вид: сначала она идет какое-то время по оси х: ŷ₁ = ... = ŷ_s = 0, а затем поднимается вверх, следуя правилу (8). А именно, из соотношения

определяется φ_s+1, из соотношения

определяется φ_s+2 и т. д.

Выпишем выражение силы сопротивления N-звенной ломаной непосредственно через ординаты вершин ломаной. Для этого в формуле (7) сделаем замену:

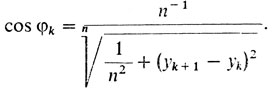
Получим после очевидных преобразований:

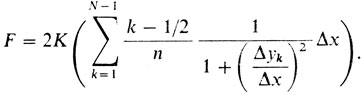
Здесь Δy_k = y_k+1 - y_k, Δx = 1/n.

Вспомнив понятие интегральной суммы и заметив, что Δy_k/Δx_k ≈ f'(x_k) нетрудно поверить, что при неограниченном увеличении числа N написанная сумма стремится к интегралу:

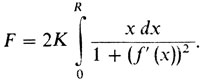(8')

Решение задачи Ньютона. Можно доказать, что при увеличении N минимальная N-звенная ломаная будет стремиться к минимальной кривой - кривой, дающей решение задачи. Это означает (если вспомнить описание минимальной N-звенной ломаной), что минимальная кривая устроена следующим образом: экстремальная функция сначала идет по оси х: f(x) = 0, 0 ≤ х ≤ а; затем она поднимается вверх по некоторой кривой (кривой Ньютона). При этом выполняется следующее соотношение:

где φ(х) - угол, образуемый касательной к графику функции y = f(х) в точке (х, f(х)). Именно в соотношение (9) перейдут равенства (8), полученные нами при решении задачи об N-звенной ломаной.

Преобразуем соотношение (9). Мы знаем (из геометрического смысла производной), что tg φ (х) = f' (х), откуда следует, что cos φ (х) = [1 + (f' (х))²]^-1/2. Таким образом, получаем

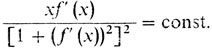(10)

Соотношение (10) есть дифференциальное уравнение для кривой Ньютона.

И, наконец, последнее. В момент а, когда горизонтальная кривая переходит в кривую Ньютона, производная кривой Ньютона равна единице (вспомним замечание Ньютона: "Небесполезное при построении судов"). Дифференциальное уравнение (10) совместно с условием, что производная в момент излома кривой равна единице, позволяет найти уравнение самой кривой Ньютона. В четырнадцатом рассказе мы это интегрирование проведем, а пока просто напишем вид кривой Ньютона. Координаты (х, y) кривой Ньютона y = f(х, с) выражаются по формулам :

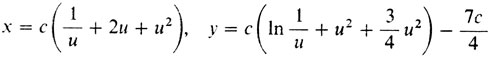(11)

через параметр u. Константа с определяется из условия f(с) = H.

Пришла пора подводить итоги. Нам надлежит ответить на несколько вопросов.

1. Как же все-таки решить задачу Ньютона? Как же построить ту кривую заданной длины и ширины, вращение которой вокруг оси будет образовывать поверхность тела, которое будет испытывать наименьшее сопротивление в редкой среде?

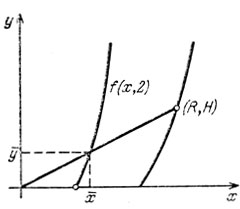
Рис. 39

Из выражения (11) видно, что совокупность всех кривых, подозреваемых на минимум, зависит от одного параметра и при этом все кривые подобны друг другу. Значит, следует поступить так, как уже было с брахистохроной. Нарисуем кривую при некотором фиксированном с, скажем, при с = 2 (см. рис. 39), Можно показать, что кривая f(х, 2) пересекается с любой прямой y = kx, k > 0 лишь один раз.

Для решения задачи Ньютона следует провести прямую y = H/R х, соединяющую начало координат с точкой (R, H). Пусть эта прямая пересечет график функции y = f(х, 2) в точке (х, y). Тогда, положив с = Н/y, построим кривую, где y = f(х, с), которая пройдет через нужную точку (R, H).

Эта кривая в семействе (11) - единственная, обладающая таким свойством. Она и будет решением задачи, поставленной Ньютоном.

2. Что же означает таинственная фраза Ньютона, которую мы процитировали в начале этого рассказа? Какое отношение имеет она к описанному выше решению задачи Ньютона?

На рис. 33 нанесены некоторые нужные нам сейчас обозначения. Мы обозначили |MN| = х, |MB| = y, | BG | = b, угол между отрезком [MN] и касательной к кривой в точке N - через φ. Этот угол равен углу HGR. Далее tg φ = f'(х). Значит,

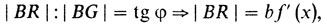
откуда

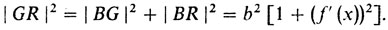
Теперь из пропорции Ньютона

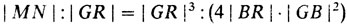
получаем

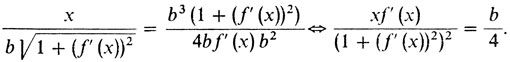(12)

Получилось дифференциальное уравнение для кривой Ньютона (ср. (10) и (12)).

Затупленность тела вращения и излом в точке G (где угол, как мы помним, равен 135°) были также предусмотрены Ньютоном. А, отвечая на первый вопрос, мы установили, что дифференциальное уравнение (12), условие в изломе, при данных ширине и длине определяют искомую кривую однозначно. Таким образом, можно считать, что аэродинамическая задача была решена Ньютоном полностью.

3. Почему же кривая Ньютона на протяжении чуть ли не трехсот лет была в положении несчастной Золушки? Почему так долго замысел Ньютона был не до конца понят?

Выше было сказано, что задача о брахистохроне открыла новую эру - эру вариационного исчисления. Вариационное исчисление бурно развивалось в течение почти двух столетий. Но, как уже говорилось, в наши дни многие технические задачи (в основном космического содержания) обнаружили, что часть актуальных проблем не может быть исследована методами вариационного исчисления. Потребовался новый шаг вперед, и была разработана новая теория - теория оптимального управления, - которая включила в себя вариационное исчисление и позволила решать задачи нового типа. Так вот, задача Ньютона относится именно к оптимальному управлению. В рамках этой теории задача Ньютона получает естественное и стандартное разрешение. А в рамках вариационного исчисления такого естественного и стандартного решения этой задачи не получалось. Таким образом, Ньютон своей задачей просто опередил время почти на 300 лет!

4. А что это за редкая среда? Бывает ли она? Не является ли абсурдным то обстоятельство, что тело наименьшего сопротивления затуплено? Кто это видывал торпеды или ракеты с затупленными головками?

Действительно, ни вода, ни окружающий нас воздух, ни любая другая привычная нам жидкая или газообразная среда не обладают свойствами редкой среды Ньютона. Так что решение Ньютона не может быть полезно при строительстве моторных лодок, катеров и океанских лайнеров. Однако физические допущения Ньютона и сама его аэродинамическая задача оказались на самом переднем крае современной науки в середине 50-х годов - в тот момент, когда настала эра сверхзвуковых и сверхвысотных летательных аппаратов. Там, "вверху" среда является "редкой". И замечание Ньютона о затупленных конусах оказалось-таки "небесполезным" при построении судов, а именно космических и сверхзвуковых. Наконец.

5. Ошибаются ли гении? В своей статье в журнале "Квант" (1982, № 5, с. 11 -18) я оставил этот вопрос без ответа. Но когда в редакции статью прочитали Андрею Николаевичу Колмогорову, он потребовал, чтобы было написано: "Конечно, ошибаются". Да, может быть, ошибаются.

Но вот неожиданный пример - задача Ньютона. Двести пятьдесят лет казалось правдоподобным, что она не имеет физической базы, а ее решение абсурдно. Но "заблуждение" гения на поверку оказалось его прозрением.

Словом, не будем торопливы: может статься, что мысль Гения, кажущаяся нам заблуждением, на самом деле несет в себе отпечаток истины - доступной ему, но еще не открывшейся нам.