Рассказ шестой. Задача Кеплера

По обе стороны от места наибольшего значения убывание вначале нечувствительно.

Кеплер

"Когда историю жизни Кеплера сопоставляешь с тем, кем он стал и что он сделал, радостно изумляешься и при этом убеждаешься, что истинный гений преодолевает любые препятствия", - писал Гёте. Мне предстоит сейчас обрисовать одного из самых лучезарных, благородных и возвышенных гениев, которые когда-либо существовали. Не располагая возможностью сколько-нибудь подробно осветить эту необыкновенную личность, я отсылаю читателя к двум книгам

о Кеплере. В книге Предтеченского "Кеплер, его жизнь и научная деятельность" [16] прекрасно отражена моральная высота Кеплера. В недавней книге Белого "Иоганн Кеплер" [3] подробно рассказано о научном подвиге и гении Кеплера. Там же приведена обширнейшая библиография. Кроме этого, на русский язык переведены две книги самого Кеплера: "Стереометрия винных бочек" [11] и "О шестиугольных снежинках".

Какие только испытания не выпадали на долю Кеплера! Бедность, лишения, болезни и смерти близких, неустроенность, скитальчество. Но когда мы читаем Кеплера, то неизменно ощущаем его благодарность судьбе - за радость и счастье, дарованные ему. Радость от труда и счастье от постижения истины. Послушаем, как он сам говорит об этом. "Я предаюсь своему энтузиазму и не стесняюсь похвалиться перед смертными своим признанием: я похитил золотые сосуды египтян, чтобы создать из них храм моему богу вдали от пределов Египта. Если вы простите мне это - я порадуюсь, если укорите меня - снесу укор. Но жребий брошен. Я пишу эту книгу. Прочтется ли она моими современниками или потомством - мне нет до этого дела - она подождет своего читателя. Разве господь бог не ждал шесть тысяч лет созерцателя своего творения?" Так говорит он о своем третьем законе движения планет. А какую радость доставляют ему открытия других! "Я сидел дома, ничего не делал и думал о вас, глубокоуважаемый и славный Галилей, как вдруг узнал об открытии вами четырех планет при помощи телескопа... Я не мог без крайнего волнения подумать, что таким образом решился наш старинный спор... Может быть, я покажусь слишком смелым, если так легко поверю твоим утверждениям, не подкрепленным никаким собственным опытом. Но почему мне не верить ученейшему математику, о правоте которого свидетельствует сам стиль его суждений?" Так пишет он Галилею, восхищаясь его открытием спутников Юпитера. Снеллиуса он называет современным Аполлонием. Сталкиваясь с трудностями при решении геометрических задач, он обращается к нему так: "Представь же нам, Снеллий, гордость геометров нашего века, строгое решение этой и прочих задач, которые тут желательны". Он искренне верит в то, что любой человек, ищущий истину, будет счастлив, узнав о ее раскрытии. К таким людям адресованы его слова: "На некоторых местах ... надо остановиться поподробнее, чтобы ... ученые люди нашли, чем воспользоваться и чему порадоваться".

Предтеченский пишет: "Он всегда остается искренним и верным себе; его высокий ум был чужд честолюбия и тщеславия, он не искал от людей ни почестей, ни похвал ... Он нисколько не выражает притязания на превосходство свое перед другими, теперь почти неизвестными учеными, и во всю жизнь относится с глубоким почтением к Местлину, замечательному в наших глазах лишь тем, что ему посчастливилось иметь такого ученика, как Кеплер ... Тихо Браге ... был принципиальным противником его, так как не принимал горячо отстаиваемой Кеплером теории Коперника; мы знаем, что между обоими этими великими людьми были личные неприятности, и тем не менее Кеплер всегда восхваляет Тихо, отдавая ему должное и не пытаясь уменьшить его заслуг... Кеплер здесь, как и всегда, является искренним другом истины, что, к сожалению, так редко встречается... в наши дни".

С полным основанием Кеплер мог сказать о себе: "Я привык везде и всегда говорить правду".

В русской литературе тема гения не нашла своего развития. Ее не касаются ни Толстой, ни Достоевский. Только Пушкин... Само слово "гений" произнесено в "Моцарте и Сальери", но чаще Пушкин пользуется еще более широким понятием - "Поэт".

Простодушие, верность дружеству, жажда творчества, способность радоваться всему прекрасному и, конечно, несовместность со злодейством - вот черты гения, которыми Пушкин наделил своего Моцарта и которыми в высшей степени обладал и Кеплер. И как Поэт, он неизменно следовал девизу: "Иди, куда влечет тебя свободный ум". Подобно тому как "Поэт сам избирает предметы своих песен", Кеплер избирал предметы своих научных изысканий.

Об одном таком "предмете" и будет наш рассказ.

Вот как описывает Кеплер событие из своей жизни, случившееся осенью 1613 года, в книге "Стереометрия винных бочек".

"В ноябре прошлого года... я ввел в свой дом новую супругу в то время, когда Австрия, закончив обильный сбор благородного винограда, распределяла свои богатства... Весь берег в Линце был завален винными бочками, продающимися по сходной цене... Поэтому ко мне на дом было принесено и поставлено несколько бочек, а через четыре дня пришел продавец и промерил подряд все кадки, без различия, не обращая внимания на форму, без всяких соображений и вычислений. Именно, медный наконечник линейки просовывался через наливное отверстие полной бочки поперек до пятки

того и другого деревянного круга, которые мы по-домашнему называем днищами, и после того, как в обоих случаях эта длина от верхней точки до нижней того и другого дощатого круга оказывалась равной, продавец объявлял количество амфор, вмещаемых бочкой, заметив лишь число на линейке в том месте, на котором оканчивалась заданная длина. Я удивился..." Кеплеру показалось странным, как с помощью одного измерения (для того чтобы его лучше понять, следует посмотреть рис. 24 из книги Кеплера) можно вычислить вместимость бочек разной формы. "Я как новобрачный счел для себя подходящим, - пишет далее Кеплер,-взять новый предмет математических занятий, и исследовать геометрические законы такого удобного в домашнем хозяйстве измерения, и выяснить его основания, если таковые имеются". Для выяснения "такого рода оснований" Кеплеру пришлось заложить основы дифференциального и интегрального исчисления, а заодно выдвинуть новые идеи для решения задач на максимум и минимум.

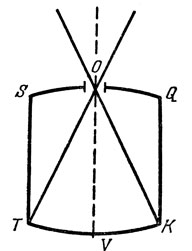
Рис. 24

Ключевое место в книге "Стереометрия винных бочек" занимает "Теорема V. [Часть вторая]. Из всех цилиндров, имеющих одну и ту же диагональ, самым большим и вместительным будет тот, в котором отношение диаметра основания к высоте равно √2".

Иначе говоря, в этой теореме дается решение следующей задачи: вписать в заданный шар цилиндр наибольшего объема. К нему естественно примыкает планиметрический вариант: вписать в заданный круг прямоугольник наибольшей площади.

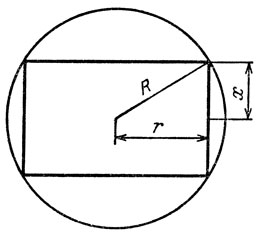
Рис. 25

Первую из сформулированных задач мы называем далее задачей Кеплера, вторую - планиметрической задачей Кеплера.

Сначала решим задачу Кеплера методом, которым решил бы ее (если бы только поставил) Тарталья. Пусть шар имеет радиус R. Половину высоты цилиндра обозначим через х (рис. 25). Тогда радиус r основания цилиндра равен √(R² - х²) и объем цилиндра равен 2k(R² - х²)х. А у Тартальи было, как мы помним, (S² - х²)х/4. Тогда из формулы предыдущего рассказа получим, что максимальное

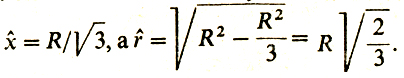
Таким образом, отношение диаметра основания экстремального цилиндра к высоте равно √2.

Но Кеплер именно так и сформулировал, как мы видели, свой результат.

Кеплер мог бы воспользоваться своей же идеей о нечувствительности изменения функции вблизи максимума (см. эпиграф к данному рассказу). Но он прошел мимо этой возможности и дал чисто геометрическое решение.

Вопрос о наиболее вместительном цилиндре, вписанном в шар, Кеплер сводит к решению следующей задачи на максимум: из всех прямоугольных параллелепипедов с квадратными основаниями, вписанных в шар, куб имеет наибольший объем^*. Этот результат доказан в теореме IV части второй книги Кеплера.

^* (Это частный случай задачи, обсуждавшейся в предыдущем рассказе)

Прямоугольные параллелепипеды с квадратными основаниями Кеплер называет коротко столбами, и мы последуем его примеру. Возможны два случая: а) столб выше куба; б) столб ниже куба.

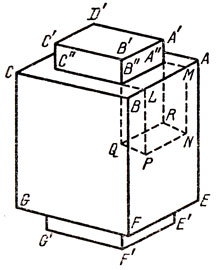
Рис. 26

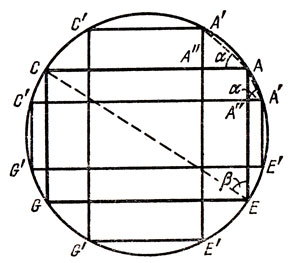
Рис. 27

Разберем сначала случай а) - см. рис. 26 и 27. Пусть куб ABCDEFGH и "столб" A'B'C'D'E'F'G'H' вписаны в одну и ту же сферу (на рис. 26 точки D, H, Н' не видны). Сравним их объемы. Из куба "выпирают" два параллелепипеда с квадратными основаниями: сверху A'B'C'D'A"B"C"D" и равный ему по объему нижний параллелепипед. При этом от куба "отнимается" гораздо больше. Усмотреть это совсем просто: у каждой стороны квадрата A"B"C"D" прилегает к столбу параллелепипед с квадратным основанием, равным (конгруэнтным) самому квадрату A"B"C"D". Один из таких параллелепипедов мы обозначили A"B"QRMNPL. Уже эти четыре параллелепипеда занимают больший объем, чем выпирающие части столба. Действительно, объем выпирающих частей равен 2|А"В"|²|А"А'|, а объем четырех прилегающих параллелепипедов равен 4|А"В"|²|А"М|. Но |А"М| = |А"А|/√2 Теперь рассмотрим треугольник А'АА" (рис. 27). Угол

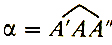
опирается на дугу А'С, угол

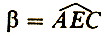
опирается на большую дугу А'С. Значит, α < β, и, следовательно,

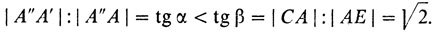
Получаем, что

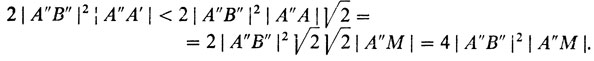
Нужное неравенство для объемов доказано.

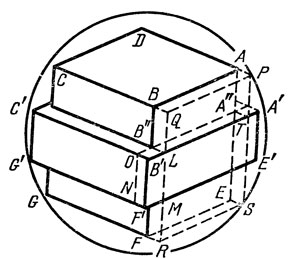
Рис. 28

Остается разобрать случай б) (рис. 28). Пусть снова куб ABCDEFGH и столб А'В'СD'Е'F'G'H' вписаны в одну и ту же сферу (точки H, D', Н' на рис. 28 не видны). Сравним их объемы. Из столба выпирают два параллелепипеда с квадратными основаниями общим объемом 2 |АВ|² |АА"|. Объем части столба, выпирающей из куба меньше. Кеплер доказывает это так. Приложим, говорит он, к каждой боковой стороне куба параллелепипед толщины, равной толщине выпирания столба. (На рис. 28 мы Рис. 28 изобразили один из четырех таких параллелепипедов ABFEPQRS.) Их общий объем равен 4|АВ|²|АP| = 4|АВ|²|A"A'|/√2. И снова, рассмотрев треугольники АА'А" и АЕС (на рис. 27), устанавливаем, что угол α больше угла β, и значит, |АА"|:|А" А'| > √2. Но, как справедливо отмечает Кеплер, если прилепить к кубу четыре параллелепипеда, то они все-таки не закроют всего столба, будут "зиять" четыре параллелепипеда у ребер (один из них - B"LB'OF"MFN (точка F" не видна) - мы изобразили на рис. 28). Каждый из этих параллелепипедов составляет часть столбиков, вытянувшихся у каждого из ребер АЕ, BF, CG и DH. Объем каждого такого столбика равен |АВ||АР|². Но когда мы приложили к каждой грани параллелепипед, то они "выдаются за высоту столба восемью столбиками" (один из этих восьми - BQPATA"B'L - нарисован на рис. 28). Объем каждого из восьми столбиков равен |АB||АР||АА"|. Очевидно, неравенство 2 |АА"| > 2√2|А"А'| = 4|АP|, из которого следует, что четыре столбика у ребер также уступают в объеме выделяющимся восьми параллелепипедам. Итак, "выпирает" из столба объем 2|АВ|² |АА"| > 4|АВ|²|АР|, а из куба меньше, чем 4|АВ|²|АР| - 8 |АВ||АР||АА"| + 4|АВ| × |АР|² < 4|АВ|² |АР|. Итак, куб больше теряет, чем приобретает. Вспомогательная задача решена. (Вспомним, что даже несколько более общую задачу алгебраическими средствами мы исследовали в предыдущем рассказе.)

Остальное совсем просто. В каждый цилиндр можно вписать столб и отношение объема цилиндра к объему вписанного столба постоянно и равно (проверьте) π/2. Значит, наибольшим по объему является цилиндр, в который можно вписать куб. А у него отношение высоты к диаметру основания равно √2.

Доказав эту теорему, Кеплер пишет: "Отсюда ясно, что австрийские бочары как бы по здравому и геометрическому смыслу при построении бочки соблюдают правило, чтобы за радиус днища брать треть длины клепок. Именно при таком устройстве цилиндр, мысленно построенный между двумя днищами, будет иметь две половины, весьма близко подходящие к условиям теоремы V, и потому будет самым вместительным, хотя бы при постройке бочки от точных правил несколько и отступили, потому что фигуры, близкие к оптимальной, очень мало меняют свою вместимость ..., ибо по обе стороны от места наибольшего значения убывание в начале несущественно."

В заключительных словах Кеплера заложен тот основной алгоритм нахождения экстремумов, который впоследствии был оформлен в точную теорему. Сначала (для многочленов) его описал Ферма (1629 г.), а затем - Ньютон и Лейбниц - в общем виде. Он впоследствии получил название "теоремы Ферма". Много интересного о задаче Кеплера читатель может почерпнуть из статьи М. Б. Балка "Секрет старого бондаря" (Квант, 1986, № 8, с. 14).