Рассказ пятый. Максимумы и минимумы в алгебре и анализе

Алгебра щедра. Зачастую она дает больше, чем у нее спрашивают.

Даламбер

1. Задача Тартальи. Начнем наш рассказ с обсуждения следующего вопроса, который был поставлен в одном из сочинений Никколо Тартальи.

Разделить число восемь на две такие части, чтобы произведение их произведения на их разность было максимальным.

Тарталья (1500-1557) вошел в историю науки как человек, научившийся решать уравнения третьей степени.

Сделаем попытку восстановить ход рассуждений Тартальи при решении его задачи. Для этого нелишне будет сказать несколько слов об истории его замечательного открытия.

Решение уравнения х³ + рх + q = 0 (для положительного р и отрицательного q) нашел впервые итальянский математик Сципион даль Ферро, живший на рубеже XV и XVI веков. Это было время, когда корнями уравнения признавались лишь положительные корни - ни отрицательные, ни тем более комплексные в расчет не брались. Ферро не опубликовал своего открытия, но посвятил в него нескольких близких себе людей. В те времена были очень распространены "математические бои". (В наши дни эта традиция возрождена - правда, в несколько иной форме. Вместо единоборств отдельных личностей в бой вступают целые коллективы: интернаты друг с другом, победители школьной олимпиады и ее жюри и т. п.)

Один из посвященных в тайну решения уравнения третьей степени решил воспользоваться ею, чтобы одерживать верх в математических сражениях. И он, наверное, добился бы полного успеха, если бы однажды судьба не свела его с Никколо Тартальей. Тарталье было предложено решить 30 уравнений третьей степени при различных значениях р и q. Сначала Тарталья не знал, что его противник обладает тайной общего решения. Но незадолго до окончания того срока, когда необходимо было представить решения задач, Тарталья узнал об этом. Вложив все свои силы в решение проблемы, Тарталья за 8 дней до назначенного срока самостоятельно нашел этот способ. (Много подробностей обо всем этом читатель узнает из интересной книги Гиндикина [7].) Иначе говоря, он получил (вслед за Ферро) следующую формулу:

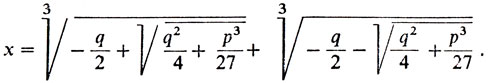(1)

Формула (1) дает выражение для положительного корня в случае Ферро (если р > 0, q < 0). Но и в других случаях (например, в том, который нам встретится дальше, когда р < 0, a q > 0) она также дает выражение для вещественного корня. Эта формула называется обычно формулой Кардано, по имени человека, впервые опубликовавшего ее. Тарталья самой формулы не опубликовал, но в ряде своих работ он сообщал о том, что умеет решать те или иные уравнения и задачи. В одном из его сочинений была поставлена и наша задача. Автор не привел ее решения, но указал ответ. Этот ответ был сформулирован так: "число 8 следует разделить пополам; квадрат этой половины, увеличенный па треть этого квадрата, должен равняться квадрату разности обеих частей". Таким образом, если искомые числа обозначить через а и b (а > b), то для разности а - b Тарталья дал такое выражение: (а - b)² = (8:2)² + (8:2)²:3 = 64/3, т.е. а - b = 8/√3 → а = 4 + 4/√3, b = 4 - 4√3. Как мы увидим дальше, Тарталья не ошибся.

А теперь попробуем (следуя книге Цейтена [20]) восстановить ход мыслей Тартальи, приведший его к правильному ответу. Не будем связывать себя с конкретным числом 8 и будем решать задачу в общем виде. Пусть требуется разделить произвольное число 5. Как мы видели, Тарталья в ответе указывает не самые числа а и b, а их разность. Наверное, именно ее он принимал за неизвестное. Итак, пусть а - Ь = х, тогда а = (S + х)/2, b = (S - х)/2, и значит, требуется найти максимум функции f(x) = х (S/2 + х/2) (S/2 - х/2) = (S²x - х³)/4. Обозначим максимальное значение этой функции (для х ≥ 0) через М. Мы пришли к уравнению для х:

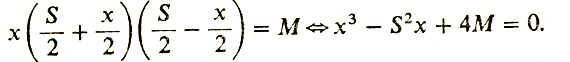(2)

К сожалению, уравнение (2) не имеет структуры уравнения Ферро, ибо здесь р = - S² < 0, a q = 4М > 0. Но, с другой стороны, уравнение (2) имеет примечательную, особенность: помимо отрицательного корня (обозначим его β) оно имеет двукратный положительный корень, т. е. здесь обращаются в нуль функция и производная. Из рис. 21 видно, что при m > М уравнение х³ - S²x + 4m = 0 не имеет положительных корней, при m < М имеет два корня, а при m = М - один положительный корень. Положительный корень уравнения (2) обозначим через α - это число и будет равно искомой разности. Таким образом, мы можем записать тождество

из которого следует, что β = 2α, р = - S² = α² - 2αβ = α² - 4α² = - 3α², q = 4М = α²β = 2³, и значит, q²/4 + р³/27 = 0 ↔ (4M)²/4 = S⁶/27 ↔ (2М)² = (S²/3)³. При этом формула (1) дает выражение для отрицательного корня:

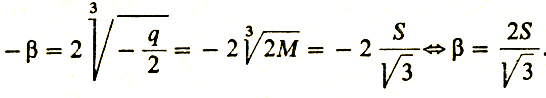
Отсюда

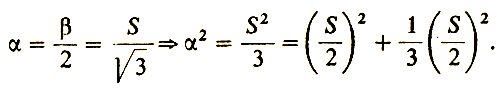
Если S = 8, то и выходит, что для получения квадрата разности "число 8 следует разделить пополам и квадрат этой половины увеличить на одну треть этого квадрата"... Задача оказалась решенной.

Много интересных задач на максимум и минимум скрыто в различного рода "точных неравенствах". Продолжим наш рассказ обсуждением, пожалуй, самого древнего такого неравенства.

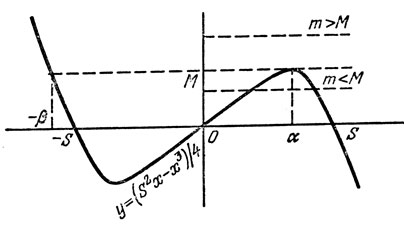
Рис. 21

2. Неравенство между средним геометрическим и средним арифметическим двух чисел. Пусть а и b - неотрицательные числа. Их средним геометрическим называется число √ab, а средним арифметическим - число (а + b)/2. Докажем, что

для любых неотрицательных чисел а и b имеет место неравенство

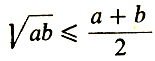(1)

т. е. что среднее геометрическое не превосходит среднего арифметического. Неравенство (1) точное. Это означает, что в (1) иногда достигается равенство, а именно это бывает тогда (и только тогда), когда а = b.

В неравенстве (1) на самом деле таятся разные экстремальные задачи. Приведем две.

А) Найти максимум произведения двух чисел, если их сумма постоянна.

Б) Найти максимальную плохцадь прямоугольного треугольника, если сумма длин катетов постоянна.

Из неравенства (1), в частности, вытекает, что среди прямоугольных треугольников с заданной суммой катетов максимальную площадь имеет равнобедренный треугольник.

Задача А) является алгебраической по своему содержанию, задача Б) - геометрической. Когда Ферма открыл свой метод нахождения максимумов и минимумов (о нем мы побеседуем в одиннадцатом рассказе), он изложил его в частном письме известному математику того времени Робервалю. Иллюстрацию своего метода он привел, решив задачу Б), сам же геометрический факт был известен еще античным геометрам.

Неравенство (1) можно доказать разными способами. Приведем здесь два доказательства: алгебраическое и геометрическое.

Алгебраическое решение основано на следующей цепочке очевидных неравенств:

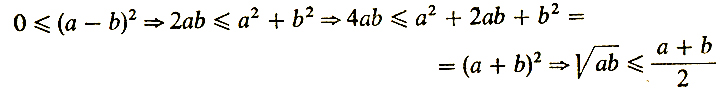
Предоставим слово геометрии (рис. 22). Возьмем отрезок длины а + b (|AD| = а, |DC| = b) и проведем полуокружность, опирающуюся на отрезок [АС]. Из точки D восставим перпендикуляр к АС. Пусть В - точка пересечения этого перпендикуляра с полуокружностью. Из подобия треугольников ABD и BCD (надо иметь в виду, что угол В опирается на полуокружность и, следовательно, - прямой, т. е. угол А равен углу DBC, а угол С равен углу ABD) получаем

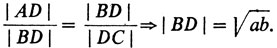
Если теперь при фиксированном отрезке [АС] (т. е. при заданной сумме а + b) менять точку D, то видно, что отрезок BD будет иметь максимальную длину (а именно равную (а + b)/2) тогда и только тогда, когда точка В совпадает с центром полуокружности. Этим и доказывается неравенство (1).

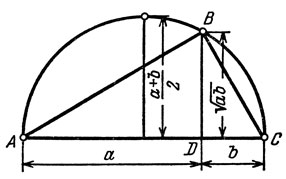
Рис. 22

3. Неравенство между средним геометрическим и средним арифметическим (общий случай).

Докажем следующую теорему.

Для любых неотрицательных чисел x₁,...,x_n неравенство

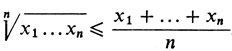(1)

Левая часть неравенства (1) называется средним геометрическим чисел x₁,...,x_n, правая называется их средним арифметическим. Таким образом, не только для n = 2, но и при любом n среднее геометрическое не превосходит среднего арифметического. Неравенство (1) является точным. Если все числа равны, оно обращается в равенство.

Существует большое число доказательств неравенства (1). Одно из самых красивых и совершенно элементарное - доказательство, данное знаменитым французским математиком О. Коши.

Сначала покажем, как по методу Коши доказать неравенство (1) для n = 3. Для этого выведем (1) при n = 4, а затем "спустимся" к n = 3. Для n = 4 неравенство (1) сразу следует из двукратного применения доказанного в предыдущем пункте неравенства (1) (для n 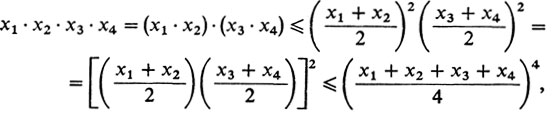= 2):

(2)

т. е. неравенство (1) для n = 4 доказано.

А теперь получаем (применив (2))

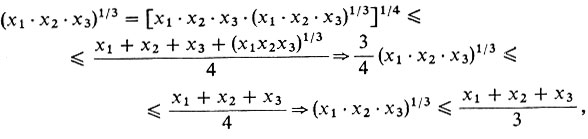
что доказывает (1) для n = 3.

Теперь докажем (1) в общем случае. Во-первых, отметим, что точно так же, как выше было доказано неравенство (1) для n = 4, можно доказать его для n = 8, затем для n = 16 и т. д. - для любого n = 2^k, k = 2, 3, ...

Применим "метод спуска", который был уже использован нами при переходе от четырех к трем. Пусть неравенство для n = m + 1 уже доказано. Докажем его для n = m. Имеем по нашему допущению

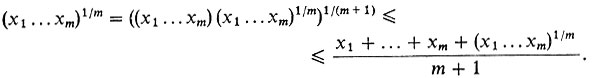
Отсюда

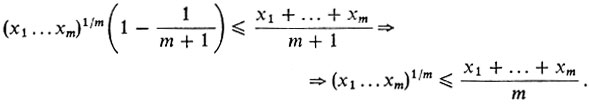
Неравенство (1) полностью доказано.

Это доказательство - одно из очень многих. В известной книге Беккенбаха и Беллмана "Неравенства" приведено двенадцать доказательств этого неравенства. Пожалуй, самое простое из них принадлежит Элерсу. Докажем по индукции, что из x₁,..., x_n = 1, x_i > 0 следует неравенство x₁ + ... + х_n (отсюда все получается очевидным образом). Для n = 1 это утверждение тривиально. Пусть для n = m утверждение доказано, и допустим, что x₁...x_m+1 = 1. Тогда имеются два числа (пусть это x₁ и х₂) такие, что x₁ ≥ 1, а х₂ ≤ 1, т. е. (x₁ - 1)(х₂ - 1) ≤ 0, или х₁х₂ + 1 ≤ x₁ + х₂. Отсюда и из допущения индукции вытекает x₁ + ... + х_m+1 ≥ 1 + x₁x₂ + х₃ + ... + x_m+1 ≥ 1 + m, что и требовалось

Неравенство между средним арифметическим и средним геометрическим издавна было любимой темой кружковых занятий. Например рассмотрим следующую задачу.

В данный шар вписать конус наибольшего объема.

Обозначим через R радиус шара и через r и h - радиус основания и высоту конуса соответственно. Тогда (продумайте это) объем V конуса равен πh² (2R - h)/3. Применяя неравенство между средним арифметическим и средним геометрическим, получим

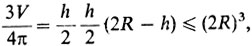
и равенство достигается при h/2 = 2R - h → h = (4/3) R. При этой высоте объем конуса и будет максимальным.

Вот еще две задачи.

Дан прямоугольный лист жести размерами а × b. Требуется вырезать около всех его углов одинаковые квадратики так, чтобы после загибания остающихся кромок получилась открытая сверху коробка наибольшей вместимости.

Впрочем, решать такие задачи нашим приемом интересно лишь до того, как научишься дифференцировать.

4. Неравенство между средним арифметическим и средним квадратическим. Пусть х₁ ..., х_n - некоторые числа. Их средним квадратическим называется число [(x²₁ ... + х²_n)/n]^1/2. Имеет место следующая теорема.

Для любых чисел х₁,...,х_n выполняется неравенство

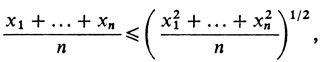(2)

т. е. среднее арифметическое всегда не превосходит среднего квадратического. Неравенство (1) является точным. Если все числа равны, оно обращается в равенство.

Неравенство (1) можно также доказывать по-разному. Но самое простое, пожалуй, такое доказательство. Имеем

Возведя среднее арифметическое в квадрат и воспользовавшись далее неравенством (2), получим

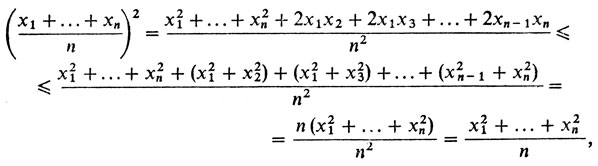
что и требовалось.

Сопоставляя неравенство между средним геометрическим и средним арифметическим и доказанное неравенство (1), получаем, что для любых неотрицательных чисел x₁,...,х_n имеет место точное неравенство

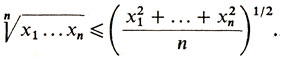(3)

В частности, при n = 2 получаем

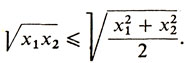
Этому неравенству можно без труда придать геометрическое содержание. Из него, например, сразу следует, что среди прямоугольников, вписанных в круг, наибольшую площадь имеет квадрат. Эта задача в свою очередь допускает по меньшей мере два стереометрических обобщения. Одно из них такое: среди прямоугольных параллелепипедов, вписанных в шар, найти параллелепипед наибольшего объема. Другое обобщение: среди цилиндров, вписанных в шар, найти цилиндр наибольшего объема. Обе эти стереометрические задачи исследовал Кеплер. Об этом будет идти речь в следующем нашем рассказе. Отметим, кстати, что из неравенства (3) при n = 3 немедленно следует, что параллелепипедом наибольшего объема, вписанным в шар, является куб. (Продумайте это!)

Планиметрическая задача о прямоугольнике наибольшей площади, вписанном в круг, также встретится нам дальше. Далее мы будем ее называть планиметрической задачей Кеплера.

5. Неравенство Коши - Буняковского. Имеет место следующая теорема:

для любых чисел a₁ ,..., a_n, b₁, ..., b_n выполнено неравенство

Неравенство (1) называется неравенством Коши - Буняковского. Оно точное: равенство достигается при а₁ = b₁ ... ..., а_n = b_n. Докажем (1). Если b₁ =... = b_n = 0, то доказывать нечего. Пусть не все b_i равны нулю. Имеем для любого числа х

где введены обозначения

Ясно, что a > 0 и что для всех х выполнено неравенство

Условие не отрицательности квадратного трехчлен (2) состоит в неравенстве

что и требовалось.

Неравенство Коши - Буняковского имеет следующее важное обобщение.

6. Неравенство Гельдера. Имеет место следующая теорема:

для любых неотрицательных чисел a₁, ..., a_n, b₁,...,b_n при р > 1 выполнено неравенство

где р' = p/(p - 1)(1/p + 1/p' = 1). Неравенство (1) называется неравенством Гельдера. Докажем его. Две функции y = х^р-1 и взаимно обратны (проверьте). Выберем два положительных числа а и b. Тогда

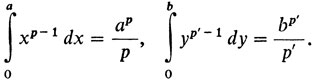
Теперь посмотрим на рис. 23. Величина а^р/р - это площадь криволинейного треугольника, заштрихованного вертикально, b^р'/р' - площадь криволинейного треугольника, заштрихованного горизонтально. Легко проверить, что при любом расположении а и b сумма площадей этих двух треугольников не меньше площади прямоугольника со сторонами а и b. Причем равенство возможно, лишь если а^p-1 = b.

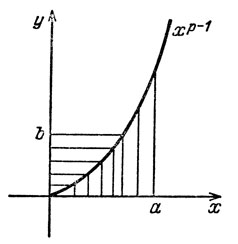
Рис. 23

Таким образом, доказано следующее неравенство для двух любых неотрицательных чисел:

Пусть теперь a₁ ,..., a_n и b₁ ,..., b_n - произвольные неотрицательные числа. Если, скажем, b₁ = ... = b_n = 0, то неравенство (1) верно. Значит, можно считать, что А = (a^p₁ + ... + a^p_n)^1/p ≠ 0 и В = (b^p'₁ + ... + b^p'_n)^1/р' ≠ 0.

Положим х_k = a_k/А, y_k = b_k/B. .Тогда из (2) следует

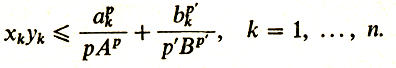
Складывая эти неравенства и учитывая, что 1/р + 1/р' = 1, а^p₁ + ... + а^p_n = А^р, b^p'₁ + ... + b^p'_n = В^p', получаем

что и требовалось.

Тема "Точные неравенства" необычайно обширна. Ей посвящено много книг и статей. Особенно известна книга Харди, Литтльвуда и Полиа [19]. Эта тема пользуется большим успехом и в популярной литературе. Как правило, применение общих методов, о которых будет рассказано во второй части, дает возможность доказывать многие точные неравенства без труда. Но бывают и исключения. Вот две задачи, которые формулируются просто, но доказательство соответствующих экстремальных свойств в них, как мне кажется, не является простым. Попробуйте вы решить их. Возможно, вы найдете какие-то совсем нетрудные решения.

Задача 1.Найти наименьшее значение суммы нечетного числа четвертых степеней величин x₁,..., x_2l+1, если известно, что их сумма и сумма их кубов равна нулю, а сумма квадратов - единице.

Задача 2. Сто положительных чисел x₁ ..., x₁₀₀ удовлетворяют условиям x²₁ + ... + x²₁₀₀₀ > 10000, x₁ + ... + x₁₀₀ < 300. Доказать, что среди них найдутся три числа, сумма которых больше 100.