
Рассказ четвертый. Максимумы и минимумы в геометрии
История науки дает нам много примеров применения чистой геометрии и пользы, приносимой ею.
Архимеда будут помнить, когда Эсхила забудут, ибо языки умирают, а математические идеи - нет.
Неиссякаемые россыпи драгоценных задач на максимум и минимум таятся в недрах древнейшей из математических наук - геометрии.
Геометрические задачи на максимум и минимум встречаются у всех трех величайших математиков античности - Евклида, Архимеда, Аполлония. Им воздавали дань крупнейшие математики эпохи Возрождения - Вивиани, Торричелли, Ферма и другие. Интерес к таким задачам сохранился до наших дней.
1. Задача Евклида. В "Началах" Евклида - первой научной монографии и первом учебном пособии в истории человечества, в труде, вышедшем в IV веке до н. э., имеется лишь одна задача на максимум. В современной редакции она выглядит так.
В данный треугольник ABC вписать параллелограмм ADEF (EF ║ АВ, DE ║ АС) наибольшей площади (рис. 12).
Приведем одно из возможных геометрических решений этой задачи, восходящее к решению Евклида, данному в "Началах".
Докажем, что искомый параллелограмм характеризуется тем, что D, Е и F - середины соответствующих сторон.
Действительно, пусть AD'E'F' - вписанный в ABC параллелограмм, отличный от ADEF. Точку пересечения прямых D'E' и EF обозначим через G', а точку пересечения прямых DE и E'F' - через G.
Покажем, что площадь параллелограмма AD'E'F' меньше площади параллелограмма ADEF на величину площади параллелограмма EG'E'G. Для этого проведем в треугольнике ABC из точки В высоту, длину которой обозначим через Я. Длину стороны АС обозначим через b, а длину высоты треугольника GE'E, проведенной из точки Е',- через Ну.
Из подобия треугольников GE'E и ABC (E'G ║ АВ, GE ║ АС) получаем
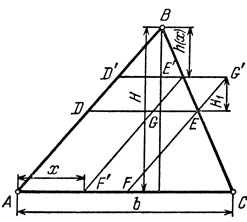
Из полученного соотношения следует, что площадь параллелограмма D'G'ED, высота которого H1, а длина стороны DE, - b/2, равна площади параллелограмма EGF'F, ибо его высота равна b/2, а длина стороны F'F равна |GE|. Отсюда и следует, что площадь параллелограмма ADEF равна площади фигуры AD'G'EGF', т. е. на величину площади параллелограмма GE'G'E больше, чем площадь AD'E'F'. Задача решена.
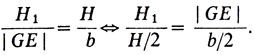
Рис. 12
2. Задача Архимеда. Мы упоминали уже, что в некоторых сочинениях древних авторов говорится, что Архимед (287 - 212 гг. до н. э.) доказывал изопериметрическое свойство окружности и изопифанное свойство сферы. Однако в дошедших до нас сочинениях Архимеда изопериметрическая задача не упоминается, и вклад Архимеда в решение этой проблемы доныне не известен. Решение же одной изопифанной задачи имеется в сочинении Архимеда "О шаре и цилиндре". Там ставится и решается следующая проблема.
Найти шаровой сегмент, вмещающий максимальный объем среди всех сегментов, имеющих заданную площадь сферической поверхности.
Приведем сначала решение, хотя целиком и основанное на идеях Архимеда, но все-таки сильно алгебраизированное. А потом мы приведем это же решение, изложенное на чисто геометрическом языке его автора.
Рассмотрим шар радиуса R и его шаровой сегмент ВАВ' высоты h (рис. 13). Наряду с сегментом ВАВ' рассмотрим полушар EDE' той же боковой поверхности. Обозначим его радиус через r. Объем V шарового сегмента равен, как мы знаем, πh2 (R - h/3), площадь его боковой поверхности равна 2πRh, объем V̂ полушара равен (2/3)r3, площадь Ŝ боковой поверхности - 2πr2. Из равенства боковых поверхностей сегмента и полушара получаем
r2 = Rh. (1)
Докажем неравенство
(2R - r)r > (2R - h)h при h ≠ R.
Рассмотрим два случая:
а) h < R и б) h > R. В случае а) r2 = Rh > h2 → r > h → R -r < R - h → (2R - r)r = R2 - (R - r)2 > R2 - (R - h)2 = (2R - h)h;
б)
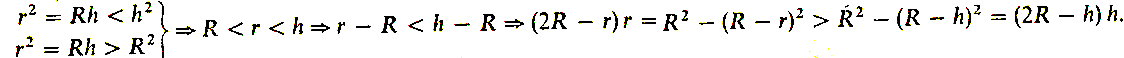
Складывая (1) и (2) и умножая на πh/3, получаем
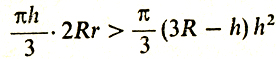 (3)
(3)Заменив теперь в (3) Rh на r2, приходим к нужному неравенству:
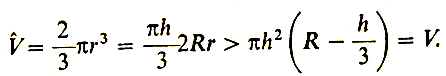
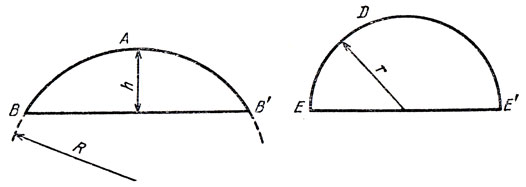
Рис. 13
Итак, полушар той же боковой поверхности имеет больший объем в сравнении с шаровым сегментом, или, говоря словами Архимеда, "из всех сферических сегментов, ограниченных равными поверхностями, наибольшим будет полушарие" (Архимед. Сочинения. - М.: Физматлит, 1962, с. 95 - 117)
Среди ученых всех времен гений Архимеда, наряду с гением Ньютона, вызывает, пожалуй, наибольшее восхищение. Не пожалеем же места и еще раз проведем решение нашей задачи, уже почти буквально следуя за мыслью Архимеда (в скобках мы все-таки указываем соответствующие алгебраические соотношения).
Архимед не мог пользоваться алгебраическим языком и алгебраическими выкладками - ведь до зарождения алгебры оставалось восемнадцать веков. Язык Архимеда - язык геометрии. На прямой А А (рис. 14) отложим, следуя Архимеду, отрезок [ОН] такой величины, чтобы конус с высотой НМ и с радиусом основания MB был бы равновелик шаровому сегменту ВАВ'. На продолжении отрезка [ОА'] отложим отрезок [А'К] равный по длине радиусу R. Равновеликость конуса и сегмента приводит Архимеда к следующей пропорции:
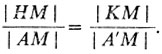 (4)
(4)Проверим, что это равенство действительно имеет место (используя известные формулы объема конуса Vk и сегмента Vc):
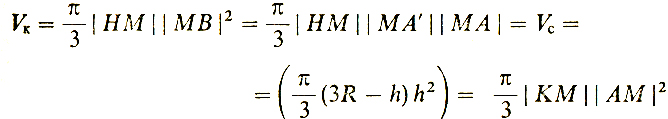 (5)
(5)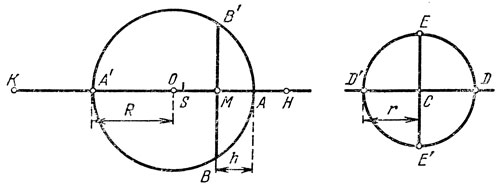
Рис. 14
Мы воспользовались тем, что длина отрезка [MB] есть среднее геометрическое длин отрезков [А'М] и [МА]. Из (5) формула (4) следует сразу.
Равенство поверхностей полушара и сегмента приводит к тому, что
|АВ| = |ED|. (6)
Действительно, |ED|=r√2, |АВ|2 = |АА'||AM| (снова - известное свойство треугольника, вписанного в окружность и опирающегося на диаметр), значит,
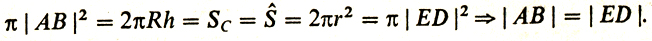
Далее Архимед откладывает отрезок [AS] равный по длине [CD] и доказывает неравенство (2):
|A'S||AS| > |А'М||AM|(↔(2R - r)r > (2 R - h) h).
Этот факт Архимед обосновывает геометрически: из двух прямоугольников с одинаковым периметром площадь больше у того, у которого больше длина меньшей стороны.
Далее имеем (из-за равенства боковых поверхностей сегмента и полушара)
|AS|2 = |AM||А'К|(↔ r2 = Rh).
Складывая последнее неравенство с этим равенством, получаем
|AS||AA'| > |KM||AM|(↔ 2Rr > (3 R - h) h).
Умножая на |AM| и используя (5), получим
|AS||АА'||АМ| > |KM||АМ|2(↔ 2Rrh > (3R - h) h2). (7)
Ранее у нас были доказаны соотношения
|KM||AM|2 = |НМ||MB|2 (см. (5)),
|АА'||АМ| = |АB|2 = |ED|2 (см. (6)),
|AS| = |CD| (по построению), откуда и из (7) получим
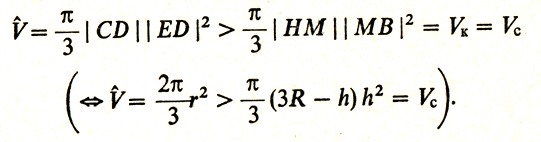
Доказательство завершено.
Может быть, нелишним будет напомнить, что все формулы, которые были использованы нами (объем конуса, шара и шарового сегмента, площадь поверхности шара и сферической поверхности сегмента), были также впервые получены именно Архимедом и все в той же работе "О шаре и цилиндре". Трудно не согласиться с Харди - Архимед будет славен, доколь жив будет хоть один математик. Со второй же частью его фразы мне не хочется соглашаться - да будет славен и Эсхил!
Разговор о задаче, составленной и решенной Аполлонием, отложим до тринадцатого рассказа.
3. Задача Штейнера.В плоскости треугольника найти точку, сумма расстояний от которой до вершин треугольника минимальна.
В иной формулировке эта задача обсуждалась в первом рассказе. Она тоже имеет давнюю историю, хотя и не такую, как героновская и классическая изопериметрическая. Она была помещена в сочинении Вивиани "О максимальных и минимальных значениях". Это был первый труд, специально посвященный нашему предмету. Он вышел в свет в 1659 году.
Этой же задачей интересовались Кавальери и Торричелли. (Само же решение в этой задаче, т. е. точку, где достигается искомый минимум, принято называть точкой Торричелли - см., например, книгу Зетеля [9]); Кокстер [10] утверждает, что нашей задачей занимался и Ферма. (Вивиани, Кавальери и Торричелли - крупнейшие итальянские ученые XVII века. Кавальери известен своим принципом - предтечей интегрального исчисления, Торричелли - открытием атмосферного давления. Торричелли и Вивиани - ученики Галилея. Именно Вивиани ослепший Галилей диктовал в конце жизни свои "Беседы о механике".)
Интерес столь крупных ученых к такой элементарной задаче - еще одно подтверждение того, что стимулом к творчеству нередко являются эстетические мотивы.
В XIX столетии этой и рядом подобных проблем много занимался Штейнер. Их часто именуют проблемами Штейнера. Так поступим и мы.
Приведем известное геометрическое решение задачи Штейнера для треугольника с углами, не превосходящими 120°.
Пусть в треугольнике ABC (рис. 15) угол С ≥ 60°. Повернем теперь треугольник ABC вокруг точки С на угол 60°. Получим треугольник А'В'С. Возьмем любую точку D в треугольнике ABC, а через D' обозначим образ D при нашем повороте. Тогда сумма длин |AD| + |BD| + |CD| равна длине ломаной |BD| + |DD'| + |D'A|.
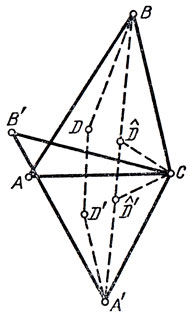
Рис. 15
Пусть теперь б - точка Торричелли, т. е. точка, из которой все стороны треугольника видны под углом 120°, и D̂' - образ D при повороте. Нетрудно понять, что точки В, D̂, D̂' и А' лежат на одной прямой, откуда следует, что точка Торричелли и является решением задачи. Отдельно нужно еще доказать, что если тупой угол больше 120°, то решением задачи будет вершина тупого угла. Сделайте это самостоятельно.?
Две задачи (четвертая и пятая) из первого рассказа примыкают к штейнеровской. Задачу 4 из первого рассказа продумайте самостоятельно. Ответ в ней таков: если точки А, В, С, D образуют выпуклый четырехугольник, то искомая точка - точка пересечения диагоналей, если не выпуклый, то это вершина наибольшего угла. Что же касается задачи 5, то ответ там отрицательный. К примеру, для квадрата имеются две экстремальные сети, изображенные нами на рис. 16. Сумма длин этих сетей меньше, чем сумма длин диагоналей.
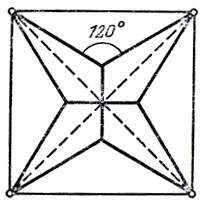
Рис. 16
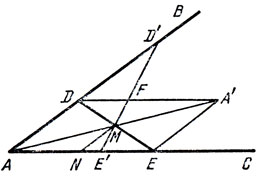
Рис. 17
Приведем еще две известные геометрические задачи на минимум.
4. Задача о наименьшей площади. Дан угол и точка внутри него. Требуется провести через эту точку прямую, отсекающую от угла треугольник наименьшей площади.
Покажем, что искомая прямая обладает тем свойством, что отрезок ее, лежащий внутри угла, делится заданной точкой пополам. Такую прямую нетрудно построить. Можно, например, соединить заданную точку М (см. рис. 17) с вершиной А, на продолжении отрезка [AM] отложить отрезок [МA'], равный по длине отрезку [AM], и провести через точку А' прямую параллельно АС. Пусть D - точка пересечения этой прямой и стороны АВ. Тогда, как легко понять, прямая, соединяющая точку D с точкой М и пересекающая АС в точке Е, обладает тем свойством, что |DM| = |ME| (ибо треугольники MDA' и ME А равны). Искомая прямая построена. Возможны и другие способы построения.
Докажем теперь, что построенная прямая действительно является искомой. Для этого проведем какую-нибудь еще прямую D'Е'. Пусть для определенности точка Е' лежит левее Е. Тогда площадь треугольника AE'D' равна площади треугольника AED минус площадь треугольника ЕМЕ' и плюс площадь треугольника MDD'. Обозначим через F точку пере
сечения прямой DM с прямой D'E'. Тогда треугольники ЕМЕ' и MDF равны. Но второй из этих треугольников содержится в треугольнике DD'M. Из сказанного вытекает, что площадь треугольника ADE меньше площади треугольника AD'E'.
5. Задача о наименьшем периметре. Дан угол и точка М внутри него. Требуется провести через эту точку прямую, отсекающую от угла треугольник наименьшего периметра.
Покажем, что искомая прямая DE обладает тем свойством, что вневписанная в треугольник ADE окружность касается отрезка [DE] в точке М. Такую прямую нетрудно построить. Впишем в угол ВАС некоторую окружность (рис. 18, а) и обозначим через М' ближайшую к А точку пересечения прямой AM с этой окружностью. Далее следует провести касательную к построенной окружности в точке М' и затем - прямую через М, параллельную этой касательной. Эта прямая и будет искомой.
А теперь докажем, что построенная прямая действительно дает решение. Проведем еще какую-нибудь прямую D'E' (рис. 18,6). Пусть вневписанная в треугольник AD'E' окружность касается отрезка D'E' в точке F, а сторон угла АВ и АС - в точках D'' и Е" соответственно. Длины отрезков [F'F] и [Е'Е"] равны как длины отрезков касательных, проведенных из одной точки. То же самое можно сказать о длинах отрезков [D'F] и [D'D"']. Значит, периметр треугольника AD'E' равен сумме длин отрезков [AD"] и [АЕ"], при этом, конечно, |AD"| = |AE"|. Таким образом, периметр треугольника AD'E' будет наименьшим, когда точки Е" и D" будут возможно близко к А. Но это произойдет как раз тогда, когда вневписанная окружность "упрется" в точку М, т. е. когда отрезок прямой, проходящей через точку M, будет касаться этой окружности в точке М.
У нас остался еще один геометрический долг: не обсуждены задачи 1 и 2 из первого рассказа. Решения этих задач ясны из рис. 19 и 20. Если же построения, изображенные на этих рисунках, невозможны, то искомые точки должны совпадать с вершиной угла.
Нашу тему исчерпать невозможно. Ей посвящено огромное количество книг. Назовем некоторые из них. Там читатель найдет любую задачу себе по вкусу. А потом, после того как он прочтет вторую часть, он сможет попытаться найти аналитические решения. Вот список книг, где имеются экстремальные задачи геометрии: Зетель [9], Кокстер [10], Курант и Роббинс [13], Шарыгин [21], [22], Шклярский, Ченцов, Яглом [23]. Специально этим вопросам посвящена статья Болтянского и Яглома [6] в "Энциклопедии элементарной математики".
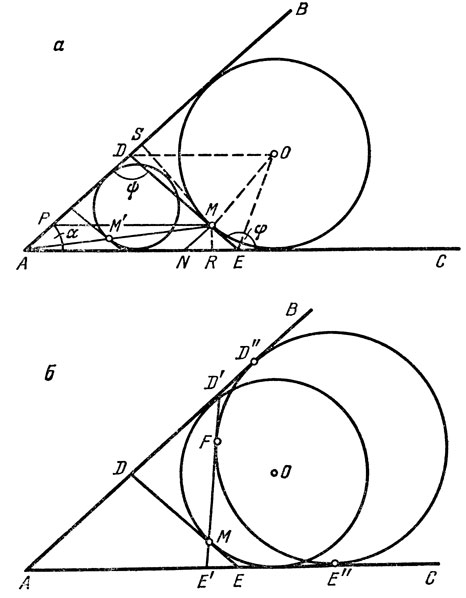
Рис. 18
Рис. 19
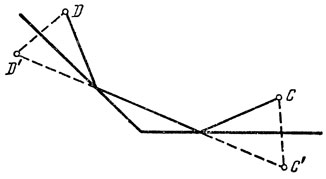
Рис. 20
В тринадцатом рассказе будет разобрано еще несколько геометрических задач.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'