Рассказ третий. Максимумы и минимумы в природе (оптика)

По Лейбницу наш мир является наилучшим из всех возможных миров, и потому его законы можно описать экстремальными принципами.

К. Зигель

Карл Зигель - выдающийся математик нашего столетия. Ему принадлежат фундаментальные результаты во многих областях математики и механики. Слова, поставленные нами выше в качестве эпиграфа, - это, конечно, шутка, но в ней содержится доля истины. У нас уже был повод при обсуждении задачи Герона отметить, что природа "руководствуется" экстремальными принципами. В первом рассказе говорилось, что при отражении от плоской поверхности она "избирает" траекторию наименьшей длины.

В словах Герона, процитированных нами в первом рассказе, содержится зародыш фундаментальной идеи, созданной в XVII - XIX веках. Тогда было уяснено, что природе свойственно "действовать" оптимально и в оптике, и в механике, и в термодинамике - вообще всюду.

Экстремальный принцип, касающийся явлений природы, был впервые четко сформулирован в оптике при попытке теоретического осмысления законов преломления света. Разнообразным оптическим проблемам, в частности истории закона о преломлении света, посвящена книга Тарасова и Тарасовой [18].

Если опустить шест в неподвижную гладь прозрачного озера, он покажется нам как бы изломанным. Это происходит из-за преломления света.

Еще древние старались найти закон преломления. В частности, во II веке до н. э. Птолемей пытался найти этот закон опытным путем. Но он не дошел до правильного ответа.

Впервые его нашел голландский ученый Снеллиус. Сейчас имя Снеллиуса не так широко известно, как имена его великих современников - Декарта, Гюйгенса и Ферма, о которых нам дальше придется говорить. Самым известным фактом, связываемым с именем Снеллиуса, так и остался открытый им экспериментально (и не опубликованный при жизни) закон преломления света. Но в свое время Снеллиус был очень знаменит: для Кеплера он был "гордостью геометров нашего века". Здесь, пожалуй, уместно напомнить, что в XVII веке

математиков называли геометрами. Вернемся, однако, к преломлению света.

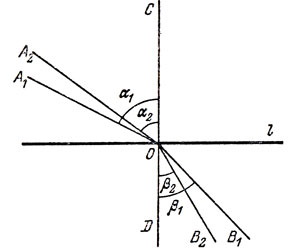
Рис. 8

Закон Снеллиуса состоит в следующем.

Пусть два луча А₁ОВ₁ и А₂ОВ₂ (идущие "сверху вниз") преломляются в точке О (рис. 8). Углы α₁ и α₂, образованные прямыми А₁О и А₂O с вертикалью ОС, называются, как мы уже знаем, углами падения. Углы β₁ и β₂, образованные прямыми В₁О и В₂O с вертикалью OD, называются углами преломления. Снеллиус установил, что

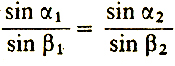
т. е. что отношение синуса угла падения к синусу угла преломления есть величина постоянная, не зависящая от угла падения.

К тому же самому закону независимо от Снеллиуса пришел Декарт - один из величайших мыслителей и ученых Франции. У нас еще будет повод (в последнем рассказе этой части) порассуждать на тему о том, "ошибаются ли гении?" Так вот, Декарт был из тех гениев, кто "ошибался". Из его "ошибок", разбросанных по ниве науки, выросли впоследствии многочисленные животворные побеги.

Так и здесь Декарт вывел закон преломления, опираясь на свои концепции о распространении световых лучей. Сами эти концепции не выдержали испытания временем, но из них выкристаллизовался впоследствии закон сохранения количества движения.

Из теории Декарта следовало, что в более плотной среде, например в воде, скорость распространения света больше, чем в менее плотной, например в воздухе.

Этот факт многим показался сомнительным. Другое объяснение закона преломления, исходя из в точности противоположной посылки (в более плотной среде свет распространяется медленнее), дал Ферма. Имя Ферма знакомо всем из-за его "великой теоремы". Ферма и Декарт были соотечественниками и современниками. Они часто спорили друг с другом в поисках научной истины. Так было и здесь. В данном случае Ферма оказался прав - экспериментально было доказано, что в более плотной среде свет распространяется медленнее.

Для объяснения закона преломления света Ферма и выдвинул экстремальный принцип для оптических явлений. Впоследствии он был назван его именем. Принцип Ферма гласит: в неоднородной среде свет избирает такую траекторию, вдоль которой время, затрачиваемое им на преодоление пути от одной точки до другой, минимально.

Принцип Ферма позволяет точно поставить и решить задачу на минимум, приводящую к выводу закона Снеллиуса. А именно этот принцип приводит к необходимости найти минимум функции одного переменного (рис. 9):

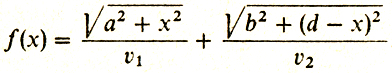(1)

Надо сказать, что к моменту, когда Ферма выдвинул свой экстремальный принцип (а это произошло около 1660 г.), он уже владел алгоритмом нахождения максимумов и минимумов функций, состоящим в приравнивании нулю производной. С помощью производных закон Снеллиуса выводится настолько просто, что его сейчас проходят даже в школе. Мы тоже повторим этот вывод в тринадцатом рассказе. Ферма же получил нужный результат гораздо более сложным путем.

Может возникнуть вопрос: почему же он не воспользовался своим алгоритмом? Ответ очень прост: в то время производных еще не было! Лейбниц не написав еще своей работы, где он ввел это понятие. Ферма мог применять свой прием только для полиномов, где он фактически предвосхитил понятие производной, а дифференцировать радикалы он не умел. И тот вывод закона Снеллиуса, который сейчас входит в школьный курс алгебры и анализа, был найден Лейбницем, причем в той же самой работе 1684 года, в которой заложен фундамент всего грандиозного строения - математического анализа.

Итак, Ферма вывел закон Снеллиуса из своего экстремального принципа, но его решение было весьма сложным. Гораздо более простое решение, основывающееся на принципе Ферма, дал Гюйгенс - еще один гениальный ученый XVII века, автор волновой теории света.

Решение Гюйгенса мы и приведем сейчас. Сначала необходимо точно поставить задачу. Она ставится так.

Даны две точки А и В по разные стороны от горизонтальной прямой l, разделяющей две среды. Требуется найти такую точку D, чтобы время преодоления пути ADB было минимальным при условии, что скорость распространения света в верхней среде υ₁, а в нижней - υ₂2 (рис. 9), Отметим, что (1) есть математическая переформулировка задачи.

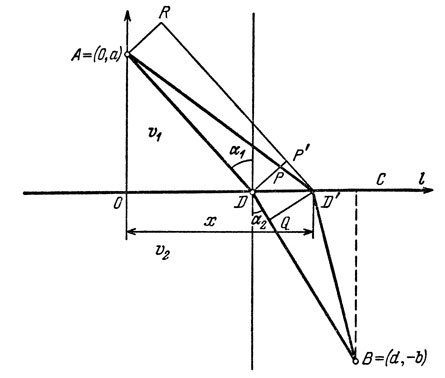
Рис. 9

Обратим внимание на сходство этой задали с задачей Герона.

Решение Гюйгенса. Пусть точка D (см. рис. 9) такова, Что в ней выполнено соотношение

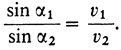(2)

Покажем, что для любой другой точки D' ≠ D время, затраченное на преодоление пути АР'В, будет больше времени, затраченного на путь ADB. Для этого восставим перпендикуляры в точках А и Р к прямой AD. Точку пересечения с AD' перпендикуляра, проведенного из точки D, обозначим через Р. Проведем прямую, параллельную AD, через точку Р', и точку пересечения этой прямой и перпендикуляра DP обозначим Р', а точку пересечения ее с перпендикуляром, проведенным из А, - через R. Наконец, опустим перпендикуляр PQ из D' на DB. Из рис. 9 видно, что величина угла PDD' равна α₁, а величина угла P'PQ равна π/₂ - α₂. Значит,

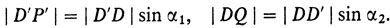(3)

Теперь проведем сравнение времен прохождения ломаных и AD'B.

Вследствие того, что |АР| > |АР|, |D'P| > |D'P'|, |D'B| > |BQ| (наклонные больше перпендикуляров), а также из (3) получаем

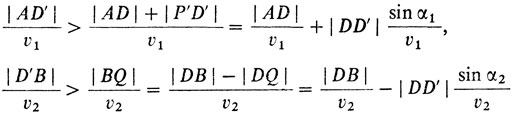
Складывая эти неравенства, получаем с учетом (2)

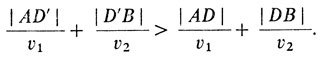
Итак, точка, преломляясь в которой, свет потратит наименьшее время на прохождение пути от А к В, характеризуется тем, что отношение угла падения к углу преломления равно υ₁/υ₂, т. е. постоянному числу. Но именно в этом и состоит закон Снеллиуса.

В основу принципа Ферма положено допущение о том, что свет распространяется по некоторым линиям. Это представление легче всего увязать с корпускулярной теорией света, согласно которой свет - это поток частиц. Гюйгенсу принадлежит еще одно объяснение законов распространения и преломления света, основанное на представлении о свете как о волне, фронт которой движется со временем.

Волновой фронт S_t - это множество точек, которых свет, распространяемый некоторым источником, может достигнуть за заданное время t. Например, если в нулевой момент времени источник - это точка, а среда однородна, то через время t фронт S_t будет сферой радиуса υt с центром в источнике света. По мере удаления от источника сферическая волна становится все более плоской, и если мы вообразим источник бесконечно удаленным, то в пределе волновой фронт окажется плоскостью, равномерно движущейся со скоростью υ.

Для определения движения волнового фронта в более сложных ситуациях Гюйгенс пользуется следующим правилом, получившим название "принцип Гюйгенса": каждая точка волнового фронта S_t сама становится вторичным источником, и через время Δt мы получаем семейство волновых фронтов от всех этих вторичных источников, и истинный волновой фронт S_t+Δt в момент t + Δt есть огибающая этого семейства (т. е. поверхность, касающаяся всех вторичных волновых фронтов) (см. рис. 10).

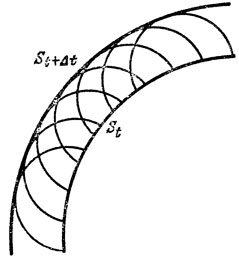
Рис. 10

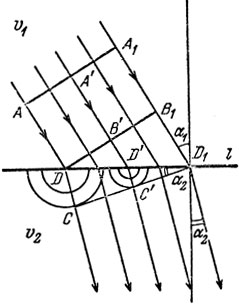
Рис. 11

Применим принцип Гюйгенса для вывода закона Снеллиуса.

Пусть параллельный пучок световых лучей падает на плоскую границу раздела двух однородных сред. Как и раньше, будем представлять себе, что l горизонтальна, а свет падает сверху (рис. 11). Через υ₁ и υ₂ (как и раньше) обозначим скорости распространения света над и под l и через α₁ и α₂ - углы падения и преломления соответственно. Волновой фронт A₁A'A движется со скоростью и в некоторый момент t волновой фронт AA₁ достигает границы l в точке D. После этого D становится вторичным источником волн, распространяющихся в нижней среде со скоростью υ₂. В точку D₁ свет придет в момент t + |B₁D₁|/υ₁ = t + (|DD₁|sinα₁)/₁ = t₁ в промежуточную точку D' на отрезке DD₁ - в момент t' = t + (|DD'|sinα₁)/₁. К моменту t¹ сферическая волна от вторичного источника D будет иметь радиус r₁ = υ₂ (t₁ - t) = |DD₁|(υ₂/υ₁)sinα₁, а волна от D' - радиус r' = υ2(t₁ - t') = |DD'|(υ₂/υ₁)sinα₁. Касательные D₁C и D₁C' к этим сферам совпадают, поскольку углы DD₁C и D'D₁C равны (так как их синусы равны соответственно r₁/|DD₁| и r'/|D'D₁| и оба числа равны (υ₂/υ₁) sin α₁ Но точка D' была взята на DD₁ произвольно, и значит, вторичные волны в момент t₁ все касаются прямой CD 1, образующей с l угол α₂ такой, что sin α₂ = (υ₂/υ₂)sinα₁. Мы снова пришли к закону Снеллиуса.

Идея "волнового фронта" может быть проиллюстрирована не только на примере оптических задач. Вот другой случай. Пусть путник начинает свой путь из точки А, лежащей на прямолинейном шоссе, ограничивающем луг. На этом лугу имеется точка В, куда путник старается попасть возможно быстрее. Скорость по лугу υ в два раза меньше скорости по шоссе. Если путник сразу пойдет по лугу, то за единицу времени он может попасть в любую точку окружности радиуса υ. Если же он все это время будет идти по шоссе, то он пройдет расстояние 2υ. Пусть он часть пути пройдет по шоссе, а часть - по лугу. Тогда множество точек, где он сможет оказаться через единицу времени, образует "волновой фронт", состоящий из двух отрезков, соединенных дугой окружности. Отсюда очень легко ответить на вопрос, как оптимально двигаться путнику.

Здесь мне представляется уместным еще раз затронуть вопрос об экстремальных принципах.

В этом рассказе были даны два вывода закона преломления света. Между ними имеется принципиальное различие. При подходе Ферма никак не проясняется истинная сущность происходящего явления. Здесь постулируется некоторое свойство траекторий и показывается, что это допущение согласуется с экспериментом. Подход Гюйгенса отталкивается от описания физической природы явления.

Такая двойственность описания типична в естествознании. Законы природы допускают, с одной стороны, истолкования, базирующиеся на некоторых физических моделях, с другой - выводятся из экстремальных принципов.

Обсуждение причин завело бы нас слишком далеко, но в связи с этим хочу отметить, что описанные в нашем рассказе два подхода сыграли важнейшую роль в истории вариационного исчисления и всей теории экстремальных задач. На самом деле любая задача вариационного исчисления и оптимального управления может быть исследована двумя путями. Можно изучать ее экстремальные траектории (подобно Ферма), и это ведет к теории Эйлера - Лагранжа (которой мы коснемся в четырнадцатом рассказе). А кроме того, есть и другой путь (Гюйгенса): изучать пучки экстремальных траекторий, что приводит к аналогам волновых фронтов, к теории, разработанной Гамильтоном и Якоби в XIX столетии, и исследованию задач оптимального управления методами динамического программирования, которые в сравнительно недалекие времена начал развивать американский ученый Беллман.