Рассказ второй. Древнейшая задача - задача Дидоны

Столько купили земли и дали ей имя Бирса,

Сколько смогли окружить бычьей шкурой.

Вергилий "Энеида"

Прекраснейшим телом является шар, а прекраснейшей плоской фигурой - круг.

Пифагор

Эпиграфом к нашему рассказу поставлены "из Энеиды два стиха" одного из величайших поэтов Древнего Рима - Публия Вергилия Марона. Как и всякое бессмертное творение, "Энеида" повествует о страстях человеческих, о добре и зле, о роке и страдании, о коварстве и любви, о жизни и смерти. Приведенные строки относятся к событию, произошедшему, если верить преданию, в IX веке до н. э. Вспомним легенду, воспроизведенную в "Энеиде".

Финикийская царевна Дидона, спасаясь от преследований своего брата, отправилась на запад вдоль берегов Средиземного моря искать себе прибежище. Ей приглянулось одно место на побережье нынешнего Тунисского залива. Дидона повела переговоры с местным предводителем Ярбом о продаже земли. Запросила она совсем немного - столько, сколько можно "окружить бычьей шкурой". Дидоне удалось уговорить Ярба. Сделка состоялась, и тогда Дидона изрезала шкуру быка на мелкие тесемки, связала их воедино и окружила большую территорию, на которой основала крепость, а вблизи от нее - город Карфаген. Там ожидали ее впоследствии неразделенная любовь и мученическая смерть.

Этот эпизод дает повод задуматься над вопросом: сколько же земли можно окружить бычьей шкурой?

Почему мы начинаем именно с этой задачи? Ведь решение ее довольно сложно. Казалось бы, следовало начинать с более простых вещей. Но я все-таки выбираю другой путь. Здесь, в этой части, я буду вести вас не от простого к сложному, а от далекого прошлого к нашим дням и потому начать хочу "с самого начала". Разве не удивительно, что в те "баснословные года" ставились и решались столь трудные и глубокие проблемы? Как мало знали наши предшественники в сравнении с тем, что знаем мы с вами! Но они шли к цели и достигали ее!

Итак, сколько же земли можно окружить бычьей шкурой? Для того чтобы ответить на этот вопрос, нужно правильно математически поставить задачу. Современный математик скажет так:

Среди замкнутых плоских кривых, имеющих заданную длину, найти кривую, охватывающую максимальную площадь.

Эту задачу и называют задачей Дидоны или классической изопериметрической задачей. (Изопериметрические фигуры - это фигуры, имеющие одинаковый периметр.)

Мы пока обошлись только словами, и человека с достаточным уровнем математической культуры такая формулировка вполне удовлетворит, ибо он знает, что такое кривая, длина и площадь. На придание же точного смысла этим словам ушло свыше двух тысяч лет. Чтобы как следует объяснить эти термины, следовало бы написать отдельную книгу. Не будем чрезмерно углубляться в это и подойдем к нашей задаче "наивно", как подходили к ней древние (и как должна была на практике подойти к ней сама царевна Дидона).

Попробуем только обойтись без шкуры быка. Отмотаем от катушки кусочек нити. Отрежем его и свяжем концами. Положим эту связанную нить на лист бумаги. Получилась плоская замкнутая кривая. Если теперь вырезать кусок бумаги по контуру нити, получится образ площади, охватываемой этой кривой. Эту площадь можно измерить. Измерение можно произвести достаточно точно, если наш лист был листом миллиметровки. Теперь уже можно понять и вопрос задачи: требуется выяснить, как следует положить нашу нить, чтобы она охватила наибольшую площадь.

Мы докажем чуть позже, что кривая, решающая классическую изопериметрическую задачу,- это окружность. Вергилий при описании действия Дидоны употребил глагол "circumdare" (окружать), содержащий корень "circus" (круг), что позволяет думать, что классическую изопериметрическую задачу сама Дидона решила правильно.

Из истории классической изопериметрической задачи. Многие историки полагают, что это - первая экстремальная задача, обсуждавшаяся в научной литературе. Вместе с изопериметрическим свойством круга (т. е. свойством окружности охватывать наибольшую площадь среди изопериметрических фигур) античные геометры отмечали изопифанное свойство шара (т. е. свойство сферы охватывать наибольший объем среди изопифанных фигур - фигур, имеющих равную площадь поверхности). С этим свойством - наибольшей вместимости - связаны представления о круге и шаре как воплощении геометрического совершенства (вспомним слова Пифагора, взятые эпиграфом к этому рассказу). Вот еще одно подтверждение той же мысли. Великая книга Н. Коперника начинается со слов: "Прежде всего мы должны заметить, что мир является шарообразным или потому, что эта форма совершеннейшая из всех и не нуждается ни в каких скрепах и вся представляет цельность, или потому, что эта форма среди всех других обладает наибольшей вместимостью, что более всего приличествует тому, что должно охватить и сохранить все".

Сейчас невозможно сказать, когда впервые была высказана мысль о наибольшей вместимости круга и шара. Во всяком случае, Аристотель (IV век до н. э.) - один из величайших мыслителей в истории человечества - пользуется этими фактами, как известными. А кто же (не считая Дидоны) на самом деле решил классическую изопериметрическую задачу? Литература, посвященная изопериметрическому свойству круга и изо-ифанному свойству шара, огромна. Из необозримого числа работ назовем одну книгу - монографию немецкого геометра В. Бляшке [4]. Там есть и указания исторического характера. Среди тех, кто дал решение изопериметрической и изопифанной задач, древние авторы называли и Архимеда. Считается, что первые строгие доказательства максимального свойства круга и шара дал Г. А. Шварц. Если вам захочется проследить "историю "изопериметрической задачи", которая началась в седой древности легендой о карфагенской царице Дидоне, до господина тайного советника Германа Амандуса Шварца из Берлина", вы можете обратиться к статье Бляшке [5] (слова, заключенные выше в кавычки, взяты из [4]).

Но на самом деле Шварцу, а до него - Вейерштрассу и после него - самому Бляшке, как и многим другим математикам XIX и XX столетий, принадлежит (в отношении классической изопериметрической задачи) лишь оформление идей своих далеких предшественников, оформление, способное удовлетворить современным требованиям строгости. Основные же пути решения изопериметрической задачи были абсолютно правильно намечены еще в античные времена. Сейчас мы расскажем об одном из таких путей, принадлежащем Зенодору - математику, жившему, как считают, где-то между III веком до н. э. и I веком н. э.

Зенодор совершенно строго, на современном уровне этого понятия, доказывает следующее утверждение.

Если существует плоский n-уголъник, имеющий наибольшую площадь среди всех n-угольников с заданным периметром, то он должен быть равносторонним и равноугольным.

Плоский n-угольник, имеющий наибольшую площадь среди всех из опериметрических с ним n-угольников, будем называть (для краткости) максимальным n-угольником. Используя этот термин, теорему Зенодора можно сформулировать короче.

Максимальный n-угольник (если он существует) должен быть правильным.

Теорема Зенодора является следствием двух лемм.

Лемма 1.Максимальный n-угольник должен быть равносторонним.

Лемма 2.Максимальный n-угольник должен быть равноугольным.

Излагая работы наших далеких предшественников, я не буду, как правило, воспроизводить их буквально, не стану сохранять обозначения и стиль авторов или стремиться приводить именно авторские доказательства. Мне хотелось бы воспроизвести лишь основное направление мысли и общий дух рассуждений, изменяя и модернизируя формулировки и доказательства. Так и здесь я приведу обработки доказательств лемм 1 и 2. При этом двукратно будет использовано решение задачи Герона.

Прежде чем приступить к доказательствам, нужно сделать одно замечание.

Следует упомянуть об обстоятельстве, не оговоренном Зейодором. Покажем, что не не выпуклый могоугольник не может быть максимальным. Действительно, если, скажем, угол А₁А₂А₃ больше 180° (рис. 2), то, отразив вершину А₂ относительно прямой А₁А₃ и рассмотрев многоугольник А₁А'₂А₃... А_n, где A'₂ - образ A₂, мы получим изопериметрический многоугольник большей площади, чем площадь A₁A₂...A_n. Теперь уже можно привести

Доказательство леммы 1. Пусть A₁A₂ ...А_n - максимальный и-угольник. Тогда он, как было отмечено, является выпуклым. Допустим, что не все его стороны имеют одинаковые длины, и придем к противоречию. Пусть две какие-либо смежные стороны, скажем, A₁A₂ и А₂А₃, не равны между собой по длине. Через вершину А₂ проведем прямую l, параллельную А₁А₃ (рис. 3). Рассмотрим задачу Герона для прямой l и точек А₁ и А₃ об определении точки D на l, для которой сумма расстояний |A₁D| + |А₃D| была бы минимальной. В предыдущем пункте было доказано, что в искомой точке D угол α равен углу β. Но угол α равен углу, а угол β равен углу DA₃A₁ по свойству накрест лежащих углов при параллельных. Таким образом, треугольник A₁DA₃ - равнобедренный и, значит, точка D отлична от точки A₂- Вместе с тем:

а) площадь ΔA₁DA₃ равна площади ΔA₁A₂A₃, ибо у них одинаковые высоты и основания;

б) сумма боковых сторон треугольника A₁DA₃ меньше суммы сторон А₁А₂ и А₂А₃, ибо D(≠А₂) есть решение задачи Герона. Построим теперь равнобедренный треугольник A₁A'₂A₃, у которого |А₁А'₂| + |А'₂А₁| = |А₁А₂| + |А₂А₃ |. Его площадь, разумеется, больше площади ΔA₁A₂A₃, так как высота |А'₂C| больше высоты |DC| (в силу того, что наклонная |A₁A'₂| длиннее наклонной |A₁D|), значит, площадь многоугольника А₁А₂...А_n больше площади изопериметрического с ним многоугольника А₁А₂ ... А_n, что противоречит максимальности последнего многоугольника. Лемма 1 доказана.

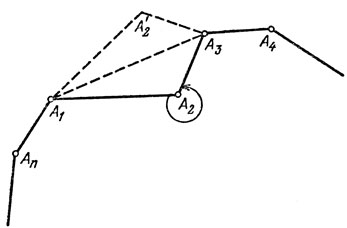
Рис. 2

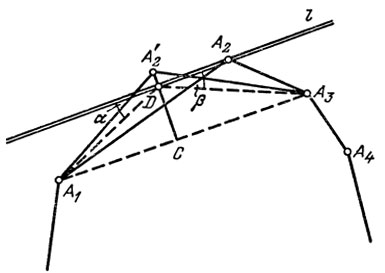
Рис. 3

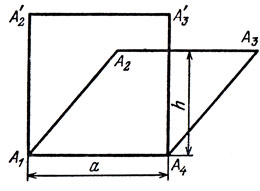
Рис. 4

Следствие. Из леммы 1 вытекает, что максимальным треугольником является равносторонний и что максимальный четырехугольник должен быть ромбом. Из последнего заключения и из рис. 4 немедленно можно вывести, что максимальный четырехугольник на самом деле - квадрат.

Доказательство леммы 2. Пусть снова А₁А₂... А_n - максимальный n-угольник. Мы уже знаем (лемма 1), что все стороны его равны, и помним, что он выпуклый. Допустим теперь, что не все его углы одинаковы, и придем к противоречию. Если не все углы равны, то существуют два неравных смежных угла α ≠ β. Докажем, что тогда существуют и два неравных не смежных угла. Рассмотрим последовательно расположенные углы многоугольника α, β, γ, δ, ε ... (их не меньше пяти). Если γ ≠ α или δ ≠ β, то мы достигли цели, так как углы α и γ (или β и δ) - не смежные. Остается рассмотреть случай α = γ, β = δ, α ≠ β, когда последовательность имеет вид α, β, δ, ε ... Но здесь не равны друг другу два не смежных угла - первый и четвертый.

Таким образом, при сделанном предположении можно считать, что существуют два не пересекающиеся внутренними частями треугольника DEF и PQR (рис. 5), каждый из которых образован подряд идущими вершинами нашего n-угольника, причем угол Е меньше угла Q. В силу того, что |DE| = |EF| = |PQ| = |QR| и из-за неравенства между углами, получаем, что |DF| < |PR|. Опустим из Е и Q перпендикуляры EG на DF и QT на PR. К продолжению отрезка EG приложим треугольник ЕТ'Р', равный (конгруэнтный) треугольнику QTP (точка Г переходит в Т', Р - в Р', Q - в Е). И снова рассмотрим задачу Герона для прямой T'G и точек Р' и F. Пусть S - решение задачи Герона, т. е. точка на T'G, для которой сумма расстояний от Р' до S и от S до F минимальна. В силу того, что угол Р'ЕТ' (равный половине угла Q) больше угла FEG (равного половине угла Q), точка 5 не совпадает с точкой Е (ибо углы P'ST' и FSG равны) и, более того, S лежит на отрезке EG.

Отложим теперь на прямой QT отрезок TU, равный по длине отрезку Т'S, и рассмотрим треугольники DSF и PUR. Сумма боковых сторон этих треугольников меньше суммы боковых сторон исходных треугольников DEF и PQR. Действительно,

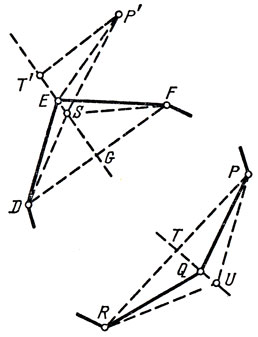
Рис. 5

Мы пользовались тем, что наши треугольники равнобедренные, и тем, что S - решение задачи Герона. С другой стороны, площадь ΔP'ES больше площади ΔESF, ибо у первого высота равна |Р'Т| = ¹/₂|PR|, у второго высота равна |FG| = ¹/₂|DF|,а по доказанному уже |DF| > |PR|. Отсюда следует, что сумма площадей треугольников DSF и PUR больше суммы площадей первоначальных треугольников DEF и PQR. Действительно,

Значит, n-угольник DSF ...PUR... имеет меньший периметр и большую площадь, чем наш изначальный n-угольник DEF... PQR... Теперь можно с любым из треугольников (DSF или PUR) поступить точно так же, как мы поступили с AA1DA3 при доказательстве леммы 1, т. е. надстроить его, уравняв периметры многоугольников и сделав площадь нового многоугольника еще большей, чем площадь многоугольника DEF... ... PQP..., следовательно, этот многоугольник - не максимальный. Лемма 2 полностью доказана, а с нею доказана и теорема Зенодора. Осталось вывести из нее решение классической изопериметрической задачи.

Лемма о существовании максимального n-угольника. Мы доказали, что если максимальный n-угольник существует, то он правильный. Но существует ли максимальный n-угольник? А вдруг нет? Тогда все пойдет прахом. А ведь не всякая функция имеет максимум. Например, функция f(х)= -(1 + х²)^-1 не достигает своего наибольшего значения (подробнее этот пример разобран в одиннадцатом рассказе).

Вопросы существования решений не были предметом рассмотрения древних авторов. Значение проблем существования и методы доказательства теорем существования были поняты примерно сто лет назад. В дальнейшем нам придется не раз касаться этих вопросов. Здесь же мы приведем без доказательства следующее утверждение (которое Зенодор, по-видимому, считал само собой разумеющимся).

Лемма 3.Максимальный n-угольник существует. Отсюда из лемм 1 и 2 следует

Теорема 1.Максимальный n-угольник является правильным n-угольником.

Теперь осталось уже совсем немного.

Завершение доказательства. Пусть Р - периметр правильного n-угольника, a S - его площадь. Мы знаем из геометрии, что Р = 2nR sin(π/n), где R - радиус описанного круга, a S = rР/2, где r - радиус вписанного круга. При этом r = R cos (π/n). Сопоставляя все это, приходим к формуле, связывающей S и Р:

Теорема 1 означает, что если Р - периметр некоторого произвольного n-угольника, а S - его площадь, то имеет место неравенство

Из неравенства tg α ≥ α (верного для 0 ≤ α < π/2) и из (2) получим неравенство

справедливое для любого n-угольника и любого n. Отметим, что для любого круга имеет место очевидное равенство

где Р - длина окружности, a S - площадь круга.

Теперь сформулируем лемму, связывающую все понятия, участвующие в формулировке классической изопериметрической задачи, с понятием n-угольника. Она означает, что длину кривой и площадь, охватываемую ею, можно с любой степенью точности приблизить длиной и площадью n-угольника.

Лемма 4.Для любой замкнутой плоской кривой длины Р*, охватывающей площадь S*, и для любого ε > 0 можно найти некоторый n-угольник, периметр Р и площадь S которого удовлетворяют неравенствам

Из леммы 4 и соотношения (4) получаем, что при любом е найдется такой многоугольник с периметром Р и площадью S, что выполнены неравенства

В силу того, что 6 произвольно, приходим к окончательному неравенству

которое согласно (5) превращается в равенство для круга.

Подытожим сказанное в виде следующего утверждения.

Теорема 2. Площадь, охватываемая любой замкнутой кривой данной длины, не превосходит площади круга, окружность которого имеет ту же длину.

Мы нашли полное решение изопериметрической проблемы.

Комментарии. 1. Полное решение нашей задачи получилось соединением двух геометрических лемм Зенодора и двух современных, но, по сути дела, технических лемм 3 и 4. Все необходимое для доказательства леммы 3 было заготовлено в трудах Вейерштрасса; понятиям длины кривой и площади, охватываемой кривой, было придано точное значение Жорданом и тем самым им были сделаны основные заготовки для доказательства леммы 4.

2. Подробное проведение доказательств лемм 3 и 4 можно прочитать в цитировавшейся книге Бляшке [4].

Но прежде, чем закончить этот рассказ, - еще одно отступление.

Доказательство Штейнера. Трудно удержаться и наряду с доказательством, восходящим к идеям древних, не предложить схему еще одного доказательства, основная мысль которого принадлежит Якобу Штейнеру, математику, обогатившему геометрию многими замечательными идеями. Доказательство Штейнера неявно подразумевает, что искомая кривая, решающая изопериметрическую задачу, существует. (А мы ведь уже знаем, что это действительно так.) Остается доказать, что эта экстремальная кривая - окружность.

Утверждение 1.Экстремальная кривая выпукла.

Что такое выпуклая кривая? Это такая кривая, что если взять любые две точки, лежащие в области, ограниченной этой кривой, то и весь отрезок, соединяющий две точки, будет лежать внутри кривой.

Заметим кстати, что выпуклость играет большую роль в задачах на максимум и минимум. О ней у нас еще пойдет речь дальше. Выпуклости посвящено много замечательных книг, рассчитанных на школьников, например: Люстерник [14], Яглом и Болтянский [24] и др.

Вернемся к доказательству Штейнера и докажем утверждение 1.

Если кривая не выпукла, то на ней нашлись бы две точки А и А' такие, что обе дуги АВА и АВ'А, соединяющие точки А и А, лежат по одну сторону от прямой АА (рис. 6). Заменив одну из этих дуг ее зеркальным отражением относительно АА, получим новую кривую большей площади при той же длине.

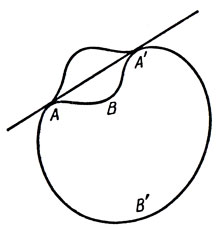
Рис. 6

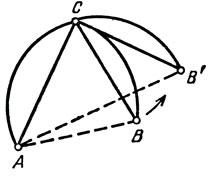
Рис. 7

Утверждение 2. Если точки А и В делят длину экстремальной линии пополам, то хорда [АВ] делит площадь фигуры пополам.

Действительно, если бы хорда [АВ] делила площадь на две неравные части, то большую часть следовало бы отразить относительно диаметра, и фигура, состоящая из большей части и ее отражения, имела бы ту же длину и большую площадь.

Утверждение 3.Пусть снова точки А и В делят длину экстремальной линии пополам и С - любая точка кривой. Тогда угол ACD - прямой.

Это центральное место. Метод, применяемый далее, носит название четырехшарнирного метода Штейнера.

Пусть имеется точка С такая, что угол АСВ не является прямым. Площадь, ограниченная дугой АСВ и диаметром АВ, разбивается на три части: треугольник ABC и сегменты, прилегающие к сторонам АС и СВ. Так вот, представим теперь себе, что в точке С у нас шарнир, соединяющий эти два сегмента. "Раздвинем" сегменты так, чтобы угол АСВ' стал прямым (рис. 7). Тогда площадь, ограниченная дугой АСВ', увеличится, ибо из всех треугольников с заданными боковыми сторонами наибольшую площадь имеет прямоугольный треугольник (так как S_ΔABC = 0,5⋅|АC|⋅|ВС|sin С ≤ 0,5|АС|⋅|ВС| и равенство достигается, если угол равен 90°). А теперь отразим полученную фигуру относительно АВ'. В итоге приходим к фигуре с тем же периметром и большей площадью. Утверждение доказано.

Мы пришли к следующему: экстремальная фигура - это множество точек С, из которых хорда АВ, делящая длину экстремальной линии пополам, видна под углом 90°, т. е. эта кривая - окружность.

Человек восторженный воскликнет: "Потрясающе!" Скептик же начнет придираться: "То не доказано, это надо обосновать... Попробуй докажи существование... Почему при шарнирном раздвижении части сегментов у точки С не станут пересекаться?"... Не станем отвечать на его ворчанье. Признаем: потрясающе, но требует обоснования!

Классической изопериметрической задаче посвящена значительная литература: Курант и Роббинс [19], Крыжановский [12], Радемахер и Теплиц [17].