
Рассказ первый. Зачем решают задачи на максимум и минимум?
В мире не происходит ничего, в чем бы не был виден смысл какого-нибудь максимума или минимума.
Большая часть вопросов практики приводится к задачам наибольших и наименьших величин, ... и только решением этих задач мы можем удовлетворить требованиям практики, которая везде ищет самого лучшего, самого выгодного.
...хочется дойти до самой сути.
О максимумах и минимумах мы узнаем в школе. Вот одна старинная задача, которую вы могли решать на уроках геометрии.
Даны две точки А и В по одну сторону от прямой l. Требуется найти на l такую точку D, чтобы сумма расстояний от А до D и от В до D была наименьшей (рис. 1).
Здесь надо найти наименьшее значение, т. е. минимум. Во многих задачах требуется найти максимум, т. е. наибольшее значение чего-нибудь. Оба понятия - максимум и минимум - объединяются единым термином - "экстремум", что по-латыни означает "крайнее". Задачи на отыскание максимума и минимума называются экстремальными задачами. (Почти тот же самый смысл вкладывается в название "задачи оптимизации".) Методы решения и исследования различного рода экстремальных задач составляют специальные разделы математического анализа. Они объединяются в общую главу, называемую теорией экстремальных задач.
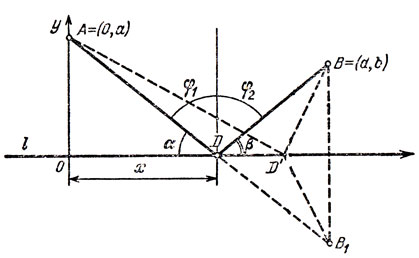
Рис. 1
Здесь наша цель - обсудить два вопроса: зачем решают задачи на максимум и минимум и из каких компонентов складывается теория экстремальных задач.
Выше была поставлена геометрическая задача. Ее можно встретить почти в каждом учебнике геометрии. Когда же она появилась впервые? И зачем?
Считают, что автором этой задачи является известный математик античности Герон Александрийский. (Далее мы называем ее задачей Герона.) О Героне мы все знаем благодаря формуле площади треугольника, носящей его имя. Книга, где помещена эта задача, называется "О зеркалах". О времени ее написания идут споры, но большинство исследователей сходятся на том, что она написана в I веке до н. э. Сам труд Герона не сохранился, и о нем известно из комментариев к нему, написанных позже. Думаю, что читатель уже слышал про задачу Герона и решал ее. Я привел ее потому, что нам она будет очень полезна для разного рода иллюстраций.
Вспомним, как решается задача Герона.
Пусть В1 - точка, симметричная В относительно прямой l Соединим А с В1. Тогда точка D пересечения АВ1 с прямой l будет искомой (см. рис. 1).
Действительно, для любой точки D' отличной от D имеет место неравенство
Здесь и в дальнейшем мы будем использовать, следующие обозначения: [АВ] - отрезок, соединяющий точки А и В, |AB| - длина отрезка [AB], AB ║ CD - прямая AB параллельна прямой CD.
В неравенстве (1) мы использовали свойства симметрии, из которых следуют равенства |DB| = |DB1|, |О'В| = |D'B1| и неравенство треугольника |AD'| + |D'B1| > |AB1|. Задача решена.
Отметим: искомая точка D обладает тем свойством, что угол α равен углу β (см. рис. 1), а также угол φ1 равен углу φ2 или, как говорят, угол падения равен углу отражения.
Попробуйте теперь, используя идею, заложенную в только что проведенном рассуждении, решить следующие задачи.
Задача 1.Дан угол и точка С внутри него. Найти точки А и В на сторонах угла так, чтобы периметр треугольника ABC был наименьшим.
Задача 2. Дан угол и две точки С и D внутри него. Найти точки А и В на сторонах угла так, чтобы сумма длин |СА| + |АВ| + |BD| была наименьшей.
Но вернемся к задаче Герона. Герон исследует в своей книге законы отражения света и прилагает итоги своих размышлений к вопросам, связанным со свойствами зеркал. В частности, он доказывает, что параболическое зеркало фокусирует пучок лучей, параллельных оси параболы.
В ту пору законы природы старались постичь умозрительно, с помощью логических рассуждений, не прибегая к эксперименту. У нас еще будет повод поговорить о зарождении современной науки, опирающейся на опыт. Первым экспериментатором в истории науки был Г. Галилей, который жил в XVII веке, Герон же при объяснении законов отражения искал для них логические основания. Он высказал предположение, что природа действует кратчайшим путем. Вот как пишет об этом один из его комментаторов Дамианос (VI век н.э.): "Герон ... показал, что прямые, наклоненные под равными углами, являются самыми меньшими из всех промежуточных, образующих наклоны с одной и той же стороны от одной и той же прямой. Доказывая это, он говорит, что если природа не хочет попусту обводить луч зрения, то она изломит их под равными углами".
Исследователи истории науки полагают, что здесь впервые прозвучала мысль о том, что природа управляется экстремальными принципами. Идею Герона развил Ферма. (На этом мы подробнее остановимся дальше - в третьем рассказе.) Ферма вывел известный к тому времени закон преломления света, исходя из допущения, что траектория распространения света от одной точки до другой в неоднородной среде характеризуется тем, что вдоль нее тратится наименьшее время. Начиная с этого момента, идея экстремальности проявлений природы становится путеводной звездой всего естествознания. В подтверждение и были приведены в качестве эпиграфа слова Эйлера.
Отложим пока обсуждение удивительности этого феномена - ведь природе невозможно приписать какую-либо цель. Тем не менее траектории света и радиоволн, движения маятников и планет, течения жидкостей и газов и многие другие движения выделяются из многообразия всех возможных тем, что они являются решениями некоторых задач на максимум или минимум. Это обстоятельство оказывается плодотворным средством математического описания природы.
Вот в чем состоит первая причина, побуждающая решать задачи на максимум и минимум и развивать теорию экстремальных задач. Она привела в XVIII веке к созданию специального раздела этой теории, который был назван вариационным исчислением.
Вторая причина кроется в нас самих. Людям свойственно стремление к лучшему, потому им всегда хочется выбрать оптимальную из имеющихся возможностей, и иногда математика может здесь помочь.
Обсудим это, и пусть снова задача Герона послужит нам примером. Иногда в учебниках ей придают вид проблемы, возникающей на практике. Тогда прямая l становится, скажем, прямолинейным участком железной дороги, точки А и В - городами, точка D - железнодорожной платформой. И ставится вопрос: где следует поставить платформу, чтобы соединяющие ее с городами прямолинейные шоссейные участки имели наименьшую суммарную длину?
Вот еще несколько геометрических задач, которые могут иметь прикладное значение. Попробуйте продумать их самостоятельно.
Задача 3.Пусть имеются три города - А, В и С, Требуется указать такое место D, чтобы суммарная длина прямолинейных участков шоссе, соединяющих D с А, В и С, была минимальной.
Задача 4.То же самое, что и в задаче 3, но для четырех городов.
Задача 5.Изменится ли решение предыдущей задачи, если поставить вопрос о наименьшей длине Шоссейной дороги, соединяющей 4 города, и при этом не уточнено, что все пути должны соединяться в одной точке?
Конечно, такого рода задачи представляют собой лишь модели реальных, жизненных ситуаций. На практике все обстоит гораздо сложнее: и участки железной дороги не бывают прямолинейными, и шоссе не строят строго по прямым, и "сумма расстояний" в чистом виде редко бывает "критерием оптимальности". Но несомненно, что и при строительстве железных, шоссейных или иных дорог, равно как и при строительстве газо- и нефтепроводов и при многом другом, обычно возникает вопрос о том, как это осуществить наиболее целесообразно, скажем, наиболее дешево.
Такие проблемы постоянно возникают в хозяйственной деятельности. Все время приходится изыскивать или самый дешевый, или самый быстрый, или самый короткий, или самый экономичный способ достижения цели.
Приведем пример проблемы оптимизации экономического содержания. Пусть имеются базы с некоторым продуктом, магазины и автопарк. Как следует диспетчеру автопарка организовать доставку необходимого продукта в магазины наиболее экономично? (Такого типа задачи называются "транспортными". Впоследствии мы уточним их постановку.) При решении сходных вопросов приходится обращаться к математике. Методы, разработанные для решения задач на максимум и минимум к середине нашего века, оказались недостаточными для решения подобных проблем.
Выяснилось, в частности, что во многих задачах экономического содержания большую роль играет понятие выпуклости - там часто встречаются выпуклые и даже линейные функции и множества. Пришлось существенно развить теорию выпуклых множеств и функций. Эта теория получила даже специальное название - выпуклый анализ. Были созданы и новые направления в теории экстремальных задач - линейное и выпуклое программирование. Начала этих направлений были заложены в 30-е годы советским математиком Л. В. Канторовичем.
Большое число задач оптимизации возникает в технике. Это задачи управления технологическими процессами, приборами, системами. Вот пример. Пусть имеется тележка, движущаяся прямолинейно без трения по горизонтальным рельсам. Тележка управляется внешней силой, которую можно изменять в заданных пределах. Требуется остановить тележку в определенном положении в кратчайшее время. Эта задача называется простейшей задачей о быстродействии в автоматическом регулировании. Очень много задач возникло в химической промышленности, в космонавтике и т. п. При этом выяснилось также, что методы вариационного исчисления недостаточны для решения этих задач. Пришлось создавать новую главу, дополняющую вариационное исчисление. Она получила название оптимального управления.
Вот и вторая причина, заставляющая нас решать задачи оптимизации и развивать теорию экстремальных задач, - желание "удовлетворить требованиям практики", о котором говорил Чебышев.
Но этими двумя причинами нельзя объяснить всего.
В следующем рассказе речь пойдет о древнейшей задаче на максимум и минимум - о классической изопериметрической задаче. Около двадцати пяти веков назад в Древней Греции было открыто замечательное свойство круга - среди замкнутых кривых заданной длины охватывать наибольшую площадь. Вы, наверное, решали в школе задачи, описывающие аналогичные свойства многоугольников. Вспомним две из них.
Задача 6.Найти треугольник заданного периметра, имеющий наибольшую площадь.
Задача 7.Доказать, что квадрат имеет наибольшую площадь среди всех прямоугольников с заданным периметром.
Вопрос, равносильный последней задаче, рассматривался еще в "Началах" Евклида; решением этой же задачи Ферма проиллюстрировал свой метод нахождения максимумов и минимумов, известный нам как теорема Ферма.
Зачем же ставились и для чего решались такие задачи? Что привлекает в них? Почему в большинстве книг по геометрии авторы так любят обсуждать задачи на максимум и минимум?
Это не так легко объяснить, но факт остается фактом, что на протяжении всей истории математики задачи на экстремум вызывали интерес и желание решать их. Может быть, все дело в том, что человеку свойственно стремление к совершенству, в том, что имеется какой-то таинственный стимул постижения "самой сути"? А может быть, в экстремальных задачах всегда или, по крайней мере, часто присутствует что- то изящное, привлекательное, нечто от той красоты, о которой говорит Рассел? И именно это побуждает нас решать задачи на максимум и минимум?
Сказанного достаточно, чтобы понять важность и увлекательность избранного нами предмета.
Но, может быть, нелишне сказать о временных границах наших рассказов. Первые задачи на максимум и минимум были поставлены в очень далекие времена: классическая изо- периметрическая задача обсуждалась в V веке до н. э. О ней мы поговорим в следующем рассказе. А в предпоследнем, четырнадцатом рассказе мы обсудим проблемы, которые возникают в наши дни.
Долгое время каждая задача на экстремум решалась индивидуально. В XVII веке явственно стала ощущаться необходимость создания каких-то общих методов. Такие методы были разработаны Ферма, Ньютоном, Лейбницем и другими - сначала для одного, потом для нескольких, а затем и бесконечного числа переменных. В итоге сформировались основные разделы теории экстремальных задач: математическое программирование, т. е. теория конечномерных задач оптимизации, выпуклое (в том числе - линейное) программирование (где изучают выпуклые задачи оптимизации), вариационное исчисление и теория оптимального управления.
Эта книга состоит из двух частей. В первой собраны старинные задачи, поставленные и решенные, как правило, до того, как были созданы первые общие методы. Во второй части рассказывается о некоторых методах теории экстремальных задач.
В первой части обсуждаются задачи, связанные с именами крупнейших математиков разных времен - Евклида, Архимеда, Ферма, Кеплера, Гюйгенса, И. Бернулли, Ньютона, Лейбница. Я не отказал себе в удовольствии "следовать за мыслями" этих великих людей.
Во второй же части... Но об этом пока еще рано говорить.
Заборы жалюзи цена с Забор.
|
ПОИСК:
|
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'