15. Комплексные особенности

Математики хорошо знают, что переход к комплексным числам обычно не усложняет, а упрощает задачу. Например, всякое алгебраическое уравнение степени n имеет ровно n комплексных корней, в то время как нахождение числа вещественных корней - нелегкая задача.

Причина этого явления состоит в следующем. Одно комплексное уравнение - это два вещественных. Множества, заданные двумя уравнениями (скажем, линии в пространстве или точки на плоскости) называются множествами коразмерности два. Множества коразмерности два не разделяют объемлющее пространство. Поэтому от любой точки пространства вне множества коразмерности два можно добраться до любой другой такой точки путем, обходящим это множество.

Рассмотрим пространство каких-либо комплексных объектов (скажем, многочленов фиксированной степени с комплексными коэффициентами). Особые объекты (скажем, многочлены с кратными корнями) определяются комплексным уравнением на коэффициенты. Следовательно, множество особых объектов имеет коразмерность два и не делит пространство всех объектов. Например, комплексный ласточкин хвост, образованный в пространстве комплексных многочленов х⁴ + ах² + bх + с многочленами с кратными корнями, не делит пространство всех таких многочленов (вещественно шестимерное).

Поэтому от любого неособого комплексного объекта (например, многочлена без кратных корней) к любому другому можно перейти непрерывным путем, оставаясь среди неособых объектов (в примере - среди многочленов без кратных корней). Но при малой деформации неоеобого объекта его топология не меняется (скажем, число корней многочлена без кратных корней не меняется при достаточно малом изменении коэффициентов). Следовательно, топологические инварианты одинаковы у всех неособых объектов данного класса (например, число комплексных корней всех многочленов данной степени без кратных корней одинаково). Итак, остается изучить топологию одного неособого комплексного объекта (найти число комплексных корней одного уравнения без кратных корней)^*, чтобы узнать топологию всех. Напротив, в вещественном случае множество особых объектов делит пространство всех объектов на части. Например, обычный ласточкин хвост (рис. 34) делит пространство вещественных многочленов х⁴ + ах² + bх + с на 3 части: в одной лежат многочлены с четырьмя вещественными корнями, в другой с двумя, в третьей - без вещественных корней (сообразите, в какой части сколько корней!).

^*(Достаточно взять уравнение (х - 1) ... (х - n) = 0; к приведенным рассуждениям остается добавить очень немного, чтобы получить вполне строгое доказательство "основной теоремы алгебры", по которой всякое уравнение степени n имеет n комплексных корней.)

Рассмотрим теперь в качестве объектов кривые, заданные на плоскости (х, у) условием f (х, у) = 0, где f - какой-либо многочлен фиксированной степени. Например, если степень равна 2, то неособая кривая будет, как правило, эллипсом или гиперболой (все другие кривые второго порядка соответствуют исключительным, особым случаям).

Множество пар комплексных чисел (х, у), удовлетворяющих уравнению f (х, у) = 0, называется комплексной кривой. С вещественной точки зрения это двумерная поверхность в четырехмерном пространстве. Как правило почти при любых коэффициентах многочлена f) комплексная кривая - неособая. Из предыдущих рассуждений следует, что все неособые кривые данной степени топологически одинаковы. Чтобы найти топологию этих поверхностей, достаточно поэтому изучить одну из неособых комплексных кривых данной степени.

Ответ оказывается таким: поверхность получается из сферы приделыванием g = (n - 1 )(n - 2)/2 ручек и выкидыванием из образовавшейся поверхности n точек. Например, комплексная прямая (n = 1) - это вещественная плоскость (сфера без одной точки), комплексная окружность - вещественный цилиндр (сфера без двух точек)" комплексная кривая степени 3 топологически устроена как поверхность тора, проколотая в трех местах.

Рис. 75. Риманова поверхность плоской алгебраической кривой

Самый простой способ в этом убедиться - получить неособую кривую небольшим шевелением из набора п прямых. Начнем, скажем, с n вещественных прямых, расположенных общим образом на плоскости и потому пересекающихся в n (n - 1)/2 точках (рис. 75). Каждая прямая задается линейным неоднородным уравнением вида l = 0, где l = ах + by + с. Перемножим соответствующие n прямым линейные функции I. Произведение обращается в нуль в точности на n прямых. Замена распадающейся на прямые кривой f = 0 на неособую кривую f = (малое число) и есть нужное шевеление.

При переходе к комплексным х и у каждая прямая становится в вещественном смысле плоскостью, так что кривая f = О превращается при комплексификации в набор n плоскостей. Каждые две такие плоскости в четырехмерном пространстве пересекаются по точке (ведь точки при комплексификации так и остаются точками). При описанном выше шевелении поверхность становится гладкой. Сглаживание устроено так: окрестность точки пересечения на каждой из обеих пересекающихся плоскостей выкидывается и затем две образовавшихся окружности склеиваются друг с другом (так, чтобы получилась ориентируемая поверхность).

Например, из трех попарно пересекающихся по точке сфер при сглаживании трех точек пересечения получается тор (рис. 75), Точно так же из п сфер получается сфера с (п - 1) (п - 2)/2 ручками, а из n плоскостей - сфера со столькими же ручками без n точек.

Тем самым мы решили задачу о топологическом строении неособой комплексной алгебраической кривой степени n (сфера с ручками, возникшая в этой конструкции, называется римановой поверхностью кривой)^*.

^*(Между прочим, из топологических свойств тора (а именно из того, что пара меридианов делит тор на две части) следует, что периоды колебаний с одинаковой полной энергией в обеих ямах механической системы с потенциальной энергией четвертой степени одинаковы (на торической римановой поверхности множества уровня энергии - фазовые кривые обеих ям - разные меридианы).)

Что же касается топологического строения вещественной кривой степени n, то оно до сих пор известно лишь для кривых малой степени (неизвестно уже, как могут располагаться ветви кривой степени 8 на плоскости).

Подобно теории кривых, теория особенностей также упрощается при переходе в комплексную область; многие явления, кажущиеся с вещественной точки зрения совершенно загадочными, в комплексной области получают прозрачное объяснение.

Рассмотрим, например, строение простейших критических точек комплексных функций (т. е. комплексификацию теории максимумов и минимумов).

Для вещественной функции критические точки связаны с перестройками линий или поверхностей уровня. Например, вещественная линия уровня х² + у² = с функции f = х² + у² пуста при с < 0и является окружностью при с > 0. Для функции х² - у² перестройка иная: асимптоты гиперболы х² - у² = c по-разному соединены ветвями этой гиперболы в зависимости от знака с. В этих примерах единственное критическое значение с = 0. Многообразия критического уровня - негладкие, некритического - гладкие.

В комплексном случае ось значений функции становится плоскостью комплексного переменного с. Критические значения лежат в этой плоскости изолированно и не делят ее на части. Поэтому многообразия уровня с при всех некритических значениям с устроены топологически одинаково. Если с, изменяясь, проходит через критическое значение, то никакой перестройки не происходит: многообразие уровня, правда, становится особым в момент прохождения с через критическое значений, но затем мгновенно возвращается в первоначальное состояние.

В комплексном случае вместо того, чтобы проходить через критическое значение, нужно обходить вокруг него (проявление общего принципа, согласно которому комплексным аналогом вещественного понятия "край" является "разветвленное накрытие").

Итак, рассмотрим на плоскости комплексного переменного с путь, обходящий критическое значение.

Каждой точке этого пути отвечает неособое многообразие уровня, f = с. При непрерывном изменении с многообразие уровня непрерывно меняется, оставаясь топологически таким же.

Иными словами, мы можем сопоставить каждой точке начального многообразия уровня близкую точку близкого многообразия уровня так, что получится взаимно-однозначное взаимно-непрерывное соответствие между обоими многообразиями уровня. Таким образом, мы получаем отождествление исходного многообразия уровня с многообразием близкого уровня с.

При непрерывном изменении с это отождествление непрерывно меняется, и в конце концов, когда с возвращается к исходному положению, мы получаем отождествление исходного многообразия уровня с самим собой. Это отождествление называется монодромией.

Итак, монодромия есть взаимно-однозначное и взаимно-непрерывное отображение многообразия неособого уровня на самого себя. Оказывается, это отображение - вовсе не тождественное преобразование: когда с делает полный оборот вокруг критического значения, возвращается на место лишь многообразие уровня с, а вовсе не его отдельные точки^*.

^*(Ситуация здесь в точности такая же, как с листом Мёбиуса. При непрерывном обходе вдоль осевой окружности листа Мёбиуса мы можем непрерывно отождествлять поперечные ей отрезки. Но когда мы впервые вернемся к исходному отрезку, полученное отождествление этого отрезка с самим собой будет менять местами его концы.)

Чтобы понять, что происходит при монодромии с точками многообразия неособого уровня, рассмотрим пример*

Изучим прежде всего многообразие неособого уровня х² + у² = с, с ≠ 0. В вещественном случае это уравнение определяет окружность, нас же интересует "комплексная окружность" - множество точек (х, у) плоскости двух комплексных переменных, сумма квадратов (комплексных) Координат которых имеет фиксированное значение.

Мы уже знаем, что эта поверхность топологически устроена как цилиндр в четырехмерном пространстве.

Оказывается, монодромия поворачивает каждую из составляющих цилиндр окружностей на свой угол, меняющийся непрерывно от нуля на одном основании до 2π на другом. Таким образом, оба края цилиндра поточечно остаются на месте, в то время как поверхность перекручивается на целый оборот, так что, например, образующая цилиндра превращается в спираль, делающую на пути от одного основания к другому полный оборот вокруг цилиндра (рис. 76).

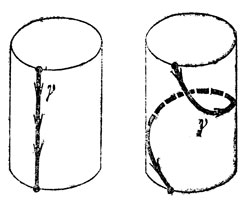
Рис. 76. Скручивание Дена - монодромия функции х² + у²

Чтобы понять, почему это так, исследуем подробнее "комплексную окружность". Уравнение ее можно записать в виде у = √с - х². Из этой формулы видно, что каждому (комплексному) значению х соответствует пара значений у, за исключением х = ± √с, - каждому из этих двух особенных значений х соответствует единственное (нулевое) значение у.

Следовательно, график комплексной "двузначной функции" у = √с - х² распростерт над плоскостью комплексной переменной х двулистно, причем оба листа соединены только в двух точках. Однако разделить оба листа, удалив лишь эти две точки, не удастся. В самом деле, заставим х обойти одну из этих точек по малому контуру, охватывающему ее один раз. Соответствующее значение у, непрерывно меняясь, вернется не к прежнему значению, а к другому. Действительно, из формулы

видно, что при обходе х вокруг одной из точек ± √с, аргумент одного из сомножителей меняется на 2π, а другого не меняется. Значит, аргумент у меняется при указанном обходе на π, т. е. у меняет знак и переходит с одного листа на другой.

При двукратном обходе х вокруг точки √с величина у возвращается к исходному значению. Точки х = ± √с называются точками ветвления функции у = √с - х².

Чтобы лучше представить себе поверхность, заданную этой функцией, соединим обе точки ветвления отрезком. Если точка х гуляет по плоскости, не пересекая этого отрезка, то у возвращается к первоначальному значению всякий раз, когда х описывает замкнутый путь. Действительно, однократный обход любой из точек ветвления меняет лишь знак у, поэтому обход всего отрезка не меняет знака у.

Ясно, что наша поверхность х² + у² = с топологически устроена как объединение двух экземпляров плоскости комплексного переменного х, разрезанной вдоль отрезка между точками ветвления, при склеивании верхнего берега разреза на каждом экземпляре с нижним берегом на другом. Топологически эта поверхность есть цилиндр. Разрез изображается на этом цилиндре экваториальной окружностью (рис. 77).

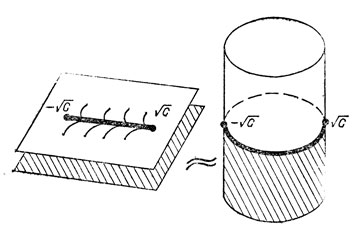
Рис. 77. Риманова поверхность кривой х² + у² = с

При приближении с к критическому значению 0 обе точки ветвления сближаются. Соединяющий их отрезок и обходящий его путь на римановой поверхности в пределе при с → 0 исчезают в критической точке. Поэтому экваториальный цикл на цилиндре х² + у² - с называют исчезающим циклом.

Для с > 0 этот исчезающий цикл - обычная вещественная окружность. Итак, мы разобрались в строении множества неособого уровня вблизи критической точки при фиксированном значении функции, близком к критическому. Вид функции при этом не важен, лишь бы критическая точка была невырожденной. Ибо все невырожденные критические точки комплексных функций топологически локально одинаковы в соответствии с объясненным выше общим принципом (комплексное вырождение накладывает два вещественных условия). В частности, топология исчезающего цикла для гиперболического случая (х² - у² = с) такая же, как для эллиптического, х² + у² = с, только в гиперболическом случае исчезающий цикл весь лежит в комплексной области.

Пусть теперь значение с обходит по малому контуру вокруг критического значения. Применим наш анализ комплексной линии уровня функции к исследованию монодромии. Если выкинуть малую окрестность особой точки, то все линии уровня (вещественные или комплексные), достаточно близкого к критическому, можно взаимно-непрерывно и взаимно-однозначно спроектировать на линию критического уровня (вне указанной окрестности особой точки, рис. 78).

Рис. 78. Отождествление соседних множеств уровня функции вдали от критических точек

Отсюда следует, что монодромия, т. е. отождествление линий уровня с, непрерывно зависящее от пути, пробегаемого значением с при обходе критического значения, может быть выбрана так, что вне указанной окрестности все точки линии уровня вернутся на место, когда с совершит полный оборот.

Остается разобраться, что произойдет внутри окрестности. При этом достаточно рассмотреть стандартную функцию f = х² + у². Часть комплексной линии уровня, попавшая внутрь окрестности, топологически представляет собой цилиндр, оба края которого выходят на границу окрестности. В то же время эта часть двулистно накрывает область на плоскости комплексного переменного х с ветвлением в точках ± √c, как это объяснено выше (рис. 77).

Когда с совершает полный оборот вокруг нуля, отрезок между точками ветвления совершает пол-оборота, в результате чего мы возвращаемся к прежним (хотя и переставившимся) точкам ветвления. Непрерывно отождествляя между собой возникающие по дороге поверхности (так, чтобы точки краев оставались все время близкими к своему исходному положению), мы получим в конце концов отображение цилиндра на себя (монодромию), устроенное следующим образом.

Отрезок образующей цилиндра, обозначенный на рисунке 79, 1 буквой γ, в процессе отождествления переходит в кривые, обозначенные этой же буквой на промежуточных поверхностях (2, 3, 4). В конце концов мы возвращаемся к исходному цилиндру (5), но кривая у переходит в новую кривую с теми же концами. Легко сообразить, что на поверхности цилиндра эта новая кривая делает один полный оборот вдоль направляющей окружности, как и изображено на рис. 76.

Рис. 79. Построение монодромии последовательным отождествлением близких римановых поверхностей

Таким образом, монодромия перекручивает цилиндрическую часть комплексной линии уровня функции, расположенную вблизи критической точки, ровно на один целый оборот. Исчезающий цикл при таком перекручивании переходит в себя (повернувшись на π). Другие же циклы на линии уровня преобразуются в, вообще говоря, новые циклы. А именно, всякий раз, когда какой-либо цикл проходил вдоль образующей нашего цилиндра (т. е. пересекал исчезающий цикл), перекручивание изменяет проходящий цикл на исчезающий, так что (с точностью до непрерывных деформаций) образ проходящего цикла при монодромии получается из проходящего цикла добавлением столько раз взятого исчезающего цикла, сколько раз проходящий цикл (с учетом знаков) пересекал исчезающий. Если это число равно нулю, то проходящий цикл называется ортогональным исчезающему. Такой цикл при монодромии не меняется.

Мы вывели, таким образом (для функций двух переменных), "формулу Пикара - Лефшеца", основную в комплексной теории критических точек функций. При переходе к функциям любого числа n переменных исчезающий цикл становится сферой размерности n - 1, а цилиндр - множеством всех его касательных векторов. Если число переменных n нечетно, то монодромия действует на классы циклов как отражение в зеркале, ортогональном исчезающему циклу (сам он при монодромии меняет знак).

Сложные критические точки функций при общих малых шевелениях распадаются на простейшие. В результате общего малого шевеления возникает несколько критических значении и около каждого из них - по исчезающему циклу. Обход каждого из критических значений определяет преобразование монодромии. Подход от некритического исходного значения к каждому критическому значению по некритическому пути переносит исчезающий цикл в многообразие исходного неособого уровня пошевеленной функции. В результате там возникает целый набор исчезающих циклов.

Например, неособая комплексная линия уровня функции х³ + у² - это тор без одной точки. Малое шевеление х³ - εх + у² имеет два критических значения (рис. 80). Подход к ним от некритической комплексной линии уровня определяет на этом торе два исчезающих цикла: параллель и меридиан тора. Точно так же на поверхности уровня функции х³ + у² + z² лежат две исчезающих сферы, пересекающиеся в одной точке. Соответствующие им преобразования монодромии - отражения пространства классов циклов в ортогональных исчезающим циклам зеркалах.

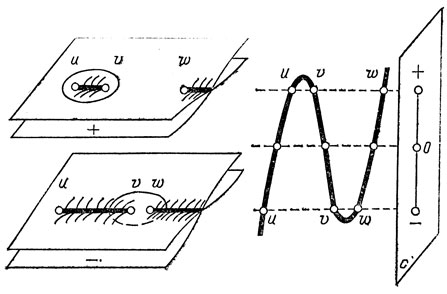
Рис. 80. Исчезающие циклы функции х³ + у²

Таким образом, в теории критических точек функций появляются группы отражений: они составляются преобразованиями монодромии при обходе вокруг критических значений.

Теория групп отражений представляет собой хорошо разработанный отдел математики. Рассмотрим, например, на плоскости два зеркала. Если угол между ними несоизмерим с 2π, то число разных преобразований, полученных комбинированием отражений в этих зеркалах, бесконечно, а если соизмерим - то конечно. Точно так же в трехмерном пространстве найдены все расположения проходящих через 0 зеркал, порождающие конечное число преобразований; классификация таких расположений известна и при любой размерности пространства.

Вычисление групп монодромий простейших вырожденных критических точек функций вскрыло глубокие связи между теориями критических точек функций, каустик и волновых фронтов, с одной стороны, и теорией групп, порожденных отражениями - с другой.

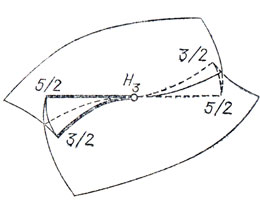
Рис.81. Дискриминант группы симметрий икосаэдра типичная особенность графики многозначной функции времени на поверхности с краем

Проявления этой связи иногда выглядят довольно неожиданно. Рассмотрим, например, задачу об обходе препятствия, ограниченного кривой общего положения с обычной точкой перегиба на плоскости. Линии уровня времени в этой задаче - эвольвенты кривой. Эти эвольвенты имеют особенности на кривой (порядка 3/2) и на касательной перегиба (порядка 5/2). Оказывается, перестройкой особенностей эвольвент при прохождении точки перегиба управляет группа симметрий икосаэдра. Отсюда выводится, например, что график функции времени в окрестности точки перегиба гладкой заменой координат приводится к нормальной форме вроде ласточкиного хвоста. А именно, нормальной формой является поверхность многочленов х⁵ + ах⁴ + bх² + с с кратными корнями (или поверхность касательных к кривой (t, t³, t⁵)A рис. 81, О. В. Ляшко, О. П. Щербак).