14. Симплектическая и контактная геометрии

Многие вопросы теории особенностей (например, классификация особенностей каустик и волновых фронтов, а также исследование всевозможных особенностей в задачах оптимизации и вариационного исчисления) становятся понятными только в рамках геометрии симплектических и контактных многообразий, освежающе непохожей на обычные геометрии Евклида, Лобачевского и Римана.

Начнем с трех примеров особенностей специального вида.

1. Градиентное отображение. Рассмотрим в евклидовом пространстве гладкую функцию. Градиентным отображением называется отображение, сопоставляющее точке значение градиента функции в ней. Градиентные отображения - весьма специальный класс отображений пространств одинаковой размерности.

Особенности градиентных отображений общего положения отличны от общих особенностей отображений пространств одинаковых размерностей: их "меньше" потому, что не всякое отображение можно реализовать как градиентное, но "больше" потому, что явление, не типичное для общих отображений, может быть типичным для градиентных.

2. Нормальное отображение. Рассмотрим множество всех векторов нормалей к поверхности в трехмерном евклидовом пространстве. Сопоставим каждому вектору его конец (вектору р, приложенному в точке q, сопоставляем точку р + q). Мы получаем отображение трехмерного многообразия векторов нормалей в трехмерное пространство (n-мерного в n-мерное, если начать с подмногообразия любой размерности в n-мерном евклидовом пространстве).

Это отображение называется нормальным отображением исходного многообразия. Особенности нормальных отображений подмногообразий общего положения составляют специальный класс особенностей отображений пространств одинаковой размерности. Критические значения нормального отображения образуют каустику (геометрическое место центров кривизны) исходного подмногообразия: см. рис. 33, где исходное многообразие - эллипс.

3. Гауссово отображение. Рассмотрим двустороннюю поверхность в трехмерном евклидовом пространстве. Перенесем единичные векторы положительных нормалей из каждой точки поверхности в начало координат. Концы этих векторов лежат на единичной сфере. Полученное отображение поверхности на сферу называется гауссовым отображением.

Гауссовы отображения составляют еще один специальный класс отображений многообразий одинаковой размерности (n - 1, если начинать с гиперповерхности в n-мерном пространстве).

И вот оказывается, что типичные особенности отображений всех этих трех классов (градиентных, нормальных и гауссовых) одинаковы: все три теории - частные случаи общей теории лагранжевых особенностей в симплектической геометрии.

Симплектическая геометрия - это геометрия фазового пространства (пространства координат и импульсов классической механики). Она явилась итогом длительного развития механики, вариационного исчисления и т. д.

В прошлом веке эту область геометрии называли аналитической динамикой, и Лагранж гордился, что изгнал из нее чертежи. Чтобы проникнуть в симплектическую геометрию, минуя длинный исторический путь, проще всего воспользоваться аксиоматическим методом, имеющим, как заметил Б. Рассел, много преимуществ, подобных преимуществам воровства перед честным трудом.

Сущность этого метода состоит в том, чтобы превращать теоремы в определения. Содержательная часть теоремы становится тогда мотивировкой определения, и алгебраисты ради повышения авторитета своей науки ее обычно опускают (понять немотивированное определение невозможно, но многие ли из пассажиров самолета знают, как и почему он изготовлен?).

Теорема Пифагора, бывшая в свое время высшим достижением математической культуры, низведена в современном аксиоматическом изложении евклидовой геометрии до малозаметного определения: евклидовой структурой в линейном пространстве называется линейная по каждому аргументу симметрическая функция пары векторов (скалярное произведение), для которой скалярный квадрат любого ненулевого вектора положителен.

Определение симплектической структуры в линейном пространстве аналогично: это линейная по каждому аргументу кососимметрическая функция пары векторов (кососкалярное произведение), которая невырождена (любой ненулевой вектор не всем векторам косоортогонален, т. е. его кососкалярное произведение с некоторыми векторами ненулевое).

Пример. Назовем кососкалярным произведением двух векторов на ориентированной плоскости ориентированную площадь параллелограмма, натянутого на эти векторы (т. е. определитель матрицы, составленной компонент векторов). Это произведение - симплектическая структура на плоскости.

В трехмерном пространстве (и вообще в нечетномерном пространстве) симплектических структур нет. Симплектическую структуру в четырехмерном (и вообще в четномерном) пространстве легко построить, представив пространство в виде суммы двухмерных плоскостей: кососкалярное произведение распадается в сумму площадей проекций на эти плоскости.

Все симплектические пространства фиксированной размерности изоморфны (как и все евклидовы). Мы будем называть кососкалярное произведение двух векторов "площадью" натянутого на них параллелограмма.

Каждое линейное пространство в евклидовом пространстве имеет ортогональное дополнение, его размерность равна коразмерности исходного подпространства.

В симплектическом пространстве определено косоортогоналыюе дополнение к линейному подпространству: оно состоит из всех векторов, кососкалярные произведения которых со всеми векторами подпространства равны нулю. Размерность косоортогонального дополнения также равна коразмерности исходного подпространства. Например, косоортогональное дополнение к прямой на плоскости - сама эта прямая.

Линейное подпространство, являющееся своим собственным косоортогональным дополнением, называется лагранжевым подпространством. Его размерность равна половине размерности исходного симплектического пространства.

Риманова структура на многообразии задается выбором евклидовой структуры в пространстве, касательном к многообразию в любой точке.

Точно так же симплектическая структура на многообразии задается выбором симплектической структуры в каждом его касательном пространстве; однако в отличие от риманова случая эти структуры не произвольны, а связаны между собой, как это объяснено ниже.

Риманова структура на многообразии позволяет измерять длины кривых на нем, суммируя длины малых векторов, составляющих кривую. Точно так же симплектическая структура позволяет измерять "площади" ориентированных двухмерных поверхностей, лежащих в симплектическом многообразии (суммируя "площади" составляющих поверхность малых параллелограммов). Дополнительное условие, связывающее симплектические структуры в разных касательных пространствах, таково: "площадь" всей границы любой трехмерной фигуры равна 0.

В линейном симплектическом пространстве можно ввести структуру симплектического многообразия, определив кососкалярное произведение приложенных в любой точке векторов как кососкалярное произведение векторов, полученных из них параллельным переносом в начало. Легко проверить, что условие согласования здесь выполнено.

Существует много неизоморфных друг другу римановых структур в окрестности точки плоскости или пространства большего числа измерений (для различения их Риман и ввел свою кривизну).

В отличие от римановых многообразий все симплектические многообразия фиксированной размерности в окрестности каждой своей точки изоморфны (отображаются друг на друга с сохранением "площадей"). Таким образом, локально каждое симплектическое многообразие изоморфно стандартному симплектическому линейному пространству. В таком пространстве можно ввести координаты (р₁, ..., р_n, q₁, ..., q_n) так, что кососкалярное произведение равно сумме ориентированных площадей проекций на плоскости (р₁, q₁), . . ., (р_n, q_n).

Подмногообразие симплектического пространства называется лагранжевым многообразием, если его касательная плоскость в каждой точке лагранжева.

Расслоение симплектического пространства на подмногообразия называется лагранжевым расслоением если слои лагранжевы.

Всякое лагранжево расслоение локально изоморфно стандартному расслоению фазового пространства над конфигурационным, (р, q) → q (слои - пространства импульсов, q = const). Конфигурационное q-пространство называется базой этого расслоения.

Предположим теперь, что в пространстве лагранжева расслоения дано еще одно лагранжево многообразие. Тогда возникает гладкое отображение этого лагранжева многообразия на базу лагранжева расслоения (т. е. на конфигурационное пространство с координатами q_i): каждой точке (р, q) лагранжева многообразия сопоставляется точка q конфигурационного пространства.

Полученное отображение многообразий одинаковой размерности n называется лагранжевым отображением, а его особенности - лагранжевыми особенностями.

Это - специальный класс особенностей гладких отображений многообразий одинаковой размерности. Для этого класса построена классификационная теория, аналогичная общей теории особенностей.

При n = 2 лагранжевы особенности общего положения исчерпываются складками и сборками, как и общие особенности (впрочем, лагранжева сборка имеет два лагранжево неэквивалентных^* варианта).

^*(Лагранжева эквивалентность двух лагранжевых особенностей - это отображение первого лагранжева расслоения на второе, переводящее первую симплектическую структуру во вторую и первое лагранжево подмногообразие во второе.)

Особенности лагранжевых отображений трехмерных лагранжевых многообразий общего положения уже не все встречаются среди обычных особенностей общего положения.

Теперь мы покажем, что градиентные, нормальные и гауссовы особенности лагранжевы.

1. Пусть F - гладкая функция от р. Тогда многообразие q = ∂F/∂p лагранжево. Поэтому особенности градиентного отображения лагранжевы.

2. Рассмотрим гладкое подмногообразие в евклидовом пространстве. Рассмотрим множество всех перпендикулярных ему векторов (во всех его точках q). Многообразие, образованное векторами р, приложенными в точках р + q, лагранжево. Нормальное отображение можно рассматривать как лагранжево отображение этого многообразия на базу, (р, р + q) → (р + q).

3. Рассмотрим многообразие всех ориентированных прямых в евклидовом пространстве. Это многообразие симплектическое, так как его можно рассматривать как фазовое пространство движения точки по сфере (направление прямой определяет точку на сфере, а точка пересечения прямой с перпендикулярной ей касательной плоскостью сферы - величину импульса).

Рассмотрим многообразие ориентированных нормалей к поверхности в нашем пространстве. Это подмногообразие в симплектическом многообразии прямых лагранжево. Гауссово отображение можно рассматривать как лагранжево отображение (отображение проектирования построенного подмногообразия на сферу, являющуюся базой лагранжева расслоения фазового пространства).

Таким образом, теории градиентных, нормальных и гауссовых особенностей сводятся к теории лагранжевых особенностей.

Встретившаяся нам в конце симплектическая структура многообразия ориентированных прямых - не столь искусственное образование, как это кажется на первый взгляд. Дело в том, что множество решений любой вариационной задачи (или вообще множество решений уравнений Гамильтона с фиксированным значением функции Гамильтона) образует симплектическое многообразие, очень полезное для исследования свойств решений.

Рассмотрим, например, двухпараметрическое семейство лучей, срывающихся с геодезических на поверхности препятствия в трехмерном пространстве, как это указано на рис, 72, Это семейство оказывается двухмерным лагранжевым подмногообразием четырехмерного пространства всех лучей. Но в отличие от ранее встречавшихся нам лагранжевых подмногообразий это лагранжево многообразие само имеет особенности. Особенности эти проявляются там, где срывающийся луч - асимптотический для поверхности препятствия, Такие лучи образуют ребро возврата (типа х² = у³) лагранжева многообразия срывающихся лучей.

На этом ребре возврата есть еще особые точки, в окрестности которых многообразие срывающихся лучей устроено как раскрытый ласточкин хвост (поверхность в четырехмерном пространстве многочленов х⁵ + ах³ + bх² + сх + d, образованная многочленами с трехкратными корнями).

Эта поверхность встречается также в других задачах теории особенностей (например, при исследовании заметания каустики ребрами возврата движущихся волновых фронтов) и является, видимо, одним из основных примеров будущей теории лагранжевых многообразий с особенностями,

В евклидовой и в римановой геометрии имеется обширная теория внешней кривизны: кроме внутренних свойств подмногообразия, определяемых его метрикой, имеются еще различия в расположении подмногообразий с одинаковыми внутренними геометриями в объемлющем пространстве.

В симплектической геометрии, как недавно доказал А. Б, Гивенталь, дело обстоит проще: внутренняя геометрия (сужение симплектической структуры на множество касательных векторов к подмногообразию) определяет внешнюю. Иными словами, подмногообразия с одинаковой внутренней геометрией локально переводятся друг в друга сохраняющим симплектическую структуру диффеоморфизмом объемлющего пространства.

Здесь открывается новая глава теории особенностей - исследование особенностей расположения подмногообразий в симплектическом пространстве, на важность которого обратил внимание Р. Мельроз в недавних работах по дифракции. Начало классификации таких особенностей получается, по теореме Гивенталя, из результатов Ж. Мартине и его последователей о вырождениях симплектической структуры. Например, двухмерное подмногообразие общего положения в четырехмерном симплектическом пространстве локально приводится сохраняющим симплектическую структуру преобразованием к одной из двух нормальных форм:

На нечетномерных многообразиях не бывает симплектических структур, но зато бывают контактные. Контактная геометрия играет для оитики и теории распространения волн такую же роль, как симплектическая для механики.

Контактная структура на нечетномерном многообразии определяется выбором в касательном пространстве в каждой точке гиперплоскости (подпространства коразмерности один). Два поля гиперплоскостей на многообразии фиксированной размерности локально эквивалентны (переводятся друг в друга диффеоморфизмом), если только оба они общего положения вблизи изучаемых точек.

Контактной структурой называется поле гиперплоскостей являющееся полем общего положения вблизи каждой точки нечетномерного многообразия.

Контактным является многообразие всех линейных элементов на плоскости. Оно трехмерно. Контактная структура задается так: скорость движения элемента принадлежит (гипер) плоскости поля, если скорость движения точки приложения принадлежит элементу. Точно так же определяется контактная структура в 2n - 1-мерном многообразии элементов гиперплоскостей на любом n-мерном многообразии.

Роль лагранжевых многообразий в контактном случае переходит к лежандровым (интегральным подмногообразиям поля гиперплоскостей наибольшей возможной размерности, т. е. размерности m в контактном многообразии размерности 2m + 1).

Особенности волновых фронтов, преобразований Лeжандра, а также гиперповерхностей, двойственных к гладким, - это лежандровы особенности. Вся симплектическая теория (включая, например, теорему Гивенталя) имеет контактные аналогу чрезвычайно полезные для исследования особенностей в вариационных задачах.

Распространение волн в сплошных средах описывается световой гиперповерхностью в контактном пространстве (называемой также "дисперсионным соотношением" или "многообразием нулей главного символа" в пространстве контактных элементов пространства-времени).

Для волн, описываемых вариационными принципами с гиперболическими уравнениями Эйлера - Лагранжа, указанная гиперповерхность, вообще говоря, имеет особенности.

Многообразие особенностей световой гиперповерхности типичной вариационной системы имеет коразмерность 3 в контактном пространстве. На трансверсальном к многообразию особенностей трехмерном пространстве световая гиперповерхность оставляет след, диффеоморфный квадратичному конусу u² + υ² = ω².

Особенности световых лучей и волновых фронтов определяются расположением световой гиперповерхности по отношению к контактной структуре (лучи - это проекции ее характеристик, а фронты - ее лежандровых многообразий). Анализ типичных расположений обнаруживает своеобразное явление внутреннего рассеяния волн на неоднородностях среды.

Обычно волны разных типов (скажем, продольные и поперечные) распространяются внутри среды независимо и лишь на границе могут порождать друг друга. Здесь же трансформация волн осуществляется во внутренних точках среды. Например, при распространении волн в одномерной нестационарной, неоднородной среде рассеяние в отдельные моменты времени испытывают отдельные лучи. Соответствующие характеристики в пространстве-времени касаются в одной точке (рис. 74).

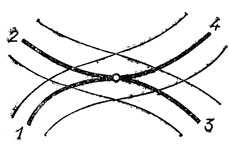
Рис. 74. Трансформация волн в одномерной среде

Кривые 1 3 и 2 4 на этом рисунке - гладкие, с касанием первого порядка. Касающиеся характеристики - это 1 4 и 2 3. На типичном волновом фронте, движущемся в трехмерном пространстве, трансформация волн происходит в отдельных изолированных точках.

За последние годы симплектическая и контактная геометрии появляются во всех отделах математики; как у каждого жаворонка должен появиться хохолок, так всякая область математики в конце концов симплектизируется. В математике есть ряд операций разных уровней: функции действуют на числа, операторы - на функции, функторы - на операторы и т. д. Симплект.изация относится к небольшому числу операций самого высшего уровня, действующих не на какие-нибудь мелочи (функции, категории, функторы), а на всю математику сразу. Хотя известно уже несколько таких операций высшего уровни (например, алгебраизация, бурбакизация, комплексификация, суперизация, симплектизация), для них нет никакой аксиоматической теории.