13. Задача об обходе препятствия

Рассмотрим в трехмерном евклидовом пространстве препятствие, ограниченное гладкой поверхностью (рис. 70). Ясно, что кратчайший путь из х в у в обход препятствия состоит из отрезков прямых и отрезков геодезических (кратчайших линий) на поверхности препятствия. На геометрию кратчайших путей сильно влияют х различные перегибы поверхности препятствия.

Рис. 70. Кратчайший путь в обход препятствия

Предположим, что начальная точка пути, х, зафиксирована, и рассмотрим кратчайшие пути, ведущие из х во всевозможные точки у. Пути в загороженные препятствием точки начинаются с отрезков касающихся препятствия прямых. Продолжения этих путей образуют пучок (однопараметрическое семейство) геодезических на поверхности препятствия. Следующие участки путей представляют собой новые отрезки прямых, касательных к геодезическим; они могут заканчиваться в концевой точке у или снова касаться поверхности препятствия и т. д.

Рассмотрим простейший случай пути, состоящего из начального и конечного отрезков прямой с отрезком геодезической между ними. Близкие геодезические пучка заполняют на поверхности препятствия некоторую область. В каждой точке этой области геодезическая пучка имеет определенное направление. В точках общего положения это направление не асимптотическое. Условие касания геодезической пучка с асимптотическим направлением - это одно условие па точку поверхности. Для поверхности и пучка общего положения это условие выполняется на некоторой кривой на поверхности (зависящей от пучка). На рис. 71 асимптотические направления изображены горизонтальными отрезками, а кривая касания обозначена буквой К; геодезические - жирные линии.

В отдельных точках (0 на рис. 71) эта кривая К сама будет иметь асимптотическое направление - это точки пересечения К с кривой ^ перегиба асимптотических (см. п. 12).

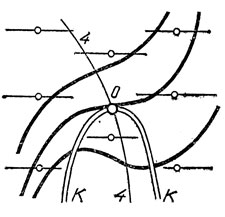
Рис. 71. Асимпототические направления и типичный пучок геодезических на поверхности

Таким образом возникает двупараметрическое семейство путей: один параметр нумерует геодезические линии пучка, другой - точку срыва касательной, уходящей с поверхности препятствия. Вдоль каждого пути определена функция времени (отсчитываемая от начальной точки х). Время достижения конечной точки у по такому пути определено не однозначно (в одну конечную точку может вести несколько таких путей), и вдобавок не все наши пути обходят препятствие. Тем не менее ясно, что исследование полученной многозначной функции времени составляет необходимый этап изучения особенностей системы кратчайших путей.

Расположим за препятствием еще одну поверхность (стенку) общего положения. и рассмотрим отображение срыва поверхности препятствия на стенку, сопоставляющее каждой точке препятствия точку пересечения срывающейся в ней касательной к геодезической пучка со стенкой.

Когда стенка удаляется на бесконечность, отображение срыва переходит в гауссово отображение пучка: каждой точке поверхности препятствия сопоставляется точка единичной сферы, а именно конец вектора длины 1, параллельного касательной к геодезической.

Отображение срыва и гауссово отображение пучка имеют особенности в точности на той линии, где направление геодезической пучка асимптотическое. Эти особенности оказываются складками в общих точках и сборками в особых точках, где направление кривой асимптотическое (О. А. Платонова).

Многозначная функция времени также имеет особенность в точках, соответствующих асимптотическому срыву. При подходящем выборе системы гладких координат функция времени приводится к виду Т = х - у^5/2 в окрестности общей точки особой поверхности у = 0. Иными словами если отметить на каждом срывающемся луче точку, отвечающую пути длины Т, то эти точки образуют поверхность фронта с ребром возврата, локально задающуюся уравнением х² = у⁵ (рис. 72).

Рис. 72. Типичная особенность фронта в задаче об обходе препятствия: ребро возврата вой - клюв степени 5/2

Аналогичный результат получается в плоской задаче (в этом случае фронты называются эвольвентами и имеют особенность типа х² = у⁵ в точках касательной перегиба (рис. 73)).

Рис. 73. Типичная особенность эвольвенты плоской кривой - клюв степени 5/2 на касательной перегиба кривой

Фронт пространственной задачи в особой точке (точке сборки гауссова отображения пучка) локально задается уравнениями

где (u, υ) - параметры, (х, у, z) - криволинейные координаты в пространстве с началом в не лежащей на поверхности препятствия точке особого асимптотического луча.