12. Гладкие поверхности и их проектирования

Гладкая кривая на плоскости может иметь касательную со сколь угодно большим числом точек касания (рис. 63), но это не в случае общего положения. Малым шевелением кривой можно добиться того, что никакая прямая не будет касаться ее более чем в двух точках.

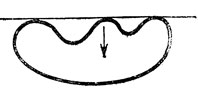
Рис. 63. Тройная касательная нетипичной кривой

В скольких точках может касаться прямой поверхность общего положения? Немного подумав или поэкспериментировав, читатель может убедиться, что наибольшее число точек касания равно четырем; сохраняя три точки касания, прямую можно двигать, две - двигать в двух направлениях.

Порядок касания прямой с кривой или поверхностью также может быть различным (например, порядок касания оси х с графиком у = х² первый, х³ - второй и т. д.) Плоская кривая общего положения не имеет касательных выше второго порядка (второй порядок касания встречается в отдельных точках кривой, называемых точками перегиба).

Для поверхности в пространстве дело обстоит уже не так просто. В точках, близ которых поверхность не выпукла, имеются касательные выше первого порядка (они называются асимптотическими касательными). Для поверхности общего положения касательные третьего порядка имеются на некоторой линии, а четвертого - в отдельных точках; касательных выше четвертого порядка общая поверхность не имеет.

Все точки поверхности общего положения делятся по порядкам касательных на следующие 7 классов (рис. 64):

1) область эллиптических точек (все касательные порядка 1);

2) область гиперболических точек (две асимптотические касательные).

Эти две области разделяет общая граница:

3) линия параболических точек (одна асимптотическая касательная).

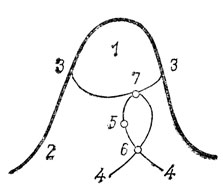
Рис. 64. Классификация точек на гладкой поверхности

Внутри области гиперболичности выделяется особая линия:

4) кривая перегиба асимптотических линий (есть касательная третьего порядка).

Наконец, на этой кривой выделены еще особые точки трех типов:

5) точка двойного перегиба касательная четвертого порядка;

6) перегиб обеих асимптотических линий (две касательные третьего порядка);

7) обилие точки линий 3) и 4).

Для поверхностей общего положения в точках 6) происходит пересечение двух ветвей линии перегибов под ненулевым углом, а в точках 7) - касание (первого порядка) линий 3) и 4).

Описанная классификация точек поверхности (О. А. Платонова, Е. Е. Ландис) следующим образом связана с классификацией особенностей волновых фронтов.

Математики называют точками объекты любой природы. Рассмотрим, например, множество всех невертикальных прямых на плоскости (х, у).

Такие прямые задаются уравнениями вида у = ах + b. Следовательно, одна прямая определяется парой чисел (а, b) и может рассматриваться как точка плоскости с координатами (а, b). Эта плоскость называется двойственной к исходной плоскости. Ее точки - это прямые исходной плоскости.

Если на исходной плоскости дана гладкая кривая, то в каждой ее точке имеется касательная прямая. При движении точки вдоль кривой касательная меняется, следовательно, движется точка двойственной плоскости. Таким образом, на двойственной плоскости возникает кривая - множество всех касательных исходной кривой. Эта кривая называется двойственной к исходной.

Если исходная кривая гладкая и выпуклая, то двойственная кривая тоже гладкая, если же исходная кривая имеет точку перегиба, то на двойственной кривой ей соответствует точка возврата (рис, 65).

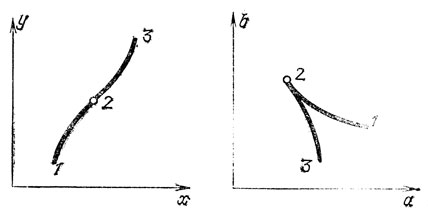
Рис. 65. Двойственность точек перегиба и возврата

Кривые, двойственные к гладким кривым общего положения, имеют такие же особенности, как волновые фронты общего положения на плоскости, и так же перестраиваются при общей гладкой деформации исходной кривой, как перестраивается распространяющийся общим образом по плоскости общий фронт.

Точно так же плоскости в трехмерном пространстве образуют двойственное трехмерное пространство, и все касательные плоскости к гладкой поверхности образуют двойственную поверхность. Особенности поверхности, двойственной к поверхности общего положения, такие же, как у волнового фронта, т. е. ребра возврата с ласточкиными хвостами.

Линии параболических точек исходной поверхности соответствует на двойственной поверхности ребро возврата. Особые точки на этой линии (где она касается линии перегиба асимптотических) соответствуют ласточкиным хвостам. Линия самопересечения ласточкиного хвоста состоит из двойных касательных плоскостей исходной поверхности. Следовательно, в точке 7) сливаются две точки касания плоскости с исходной поверхностью, чем и заканчивается однопараметрическое семейство двойных касательных плоскостей.

Классы точек на поверхности общего положения проявляются также в виде различных особенностей видимого контура. Если направление проектирования - общего положения, то особенности - лишь складки и сборки, по теореме Уитни. Однако, выбрав направление проектирования специальным образом, можно получить и некоторые не общие проекции поверхности общего положения. Оказывается, все такие проектирования локально приводятся к проектированиям перечисленных ниже 9 поверхностей z = f (х, у) вдоль оси х: (поверхности проектируются на плоскость, (у, z), приведение осуществляется заменой X (х, у, z), Y (у, z), Z (y, z)).

Видимые контуры, соответствующие этим проекциям, изображены на рис. 66.

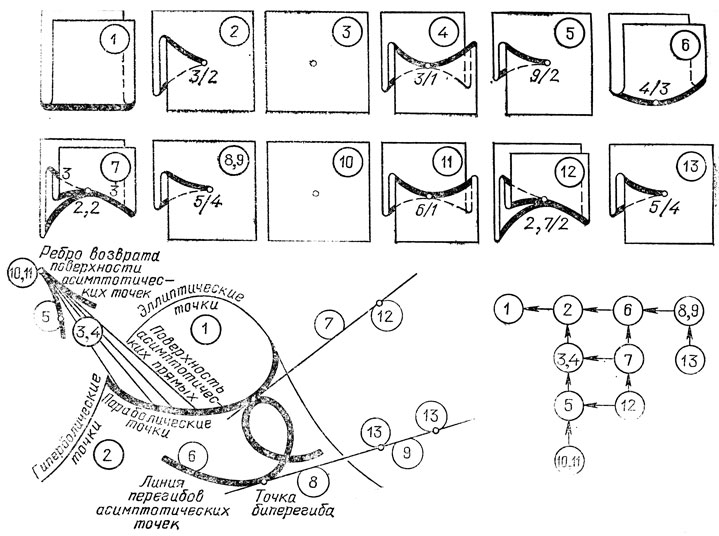
Рис. 66. Видимые контуры и порядки их особенностей для типичных проектирований

Соответствие между классификацией проектирований и точек на поверхности состоит в следующем. 1 - это проектирование по неасимптотическому направлению (складка Уитни).

Проектирование по асимптотическому направлению в общей точке гиперболической области принадлежит типу 2. Это проектирование имеет особенностью сборку Уитни. При малом шевелении направления проектирования особая точка лишь немного перемещается по поверхности: новое направление оказывается асимптотическим в близкой точке. Таким образом, чтобы увидеть сборку, достаточно взглянуть на общую поверхность по асимптотическому направлению.

При движении поверхности или наблюдателя в отдельные моменты появятся особенности 3, 4 и 6.

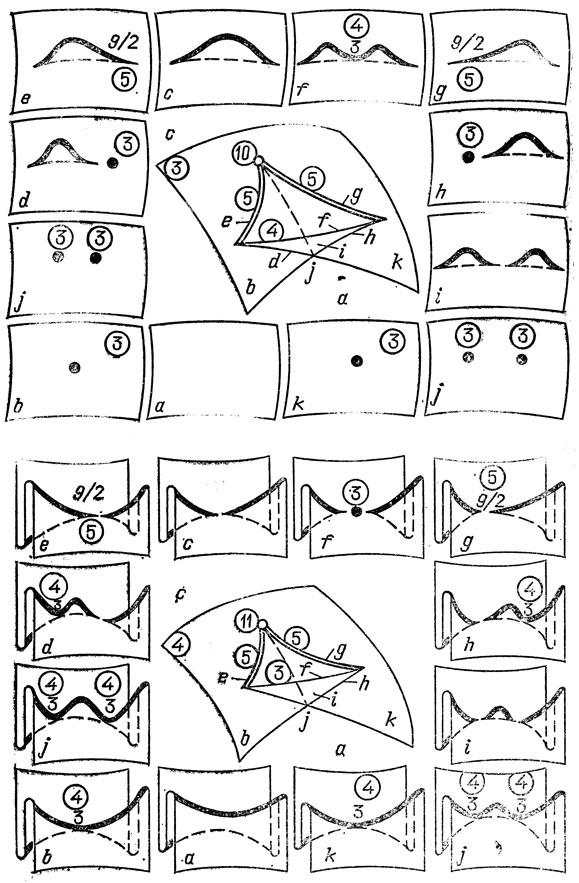
Рис. 67. Бифуркации проектирований при деформации центра проекции: случаи 10 - 11, z = х³ ± ху⁴

Проектирования 6 (и 8 или 9) соответствуют гиперболической области (а именно асимптотическим касательным третьего и четвертого порядков соответственно).

По спине двугорбого верблюда (см. рис. 43) проходит линия перегиба асимптотических. Касательные третьего порядка, приложенные в ее точках, образуют поверхность. Проходя мимо верблюда, мы дважды пересекаем эту поверхность. В момент пересечения видимый контур спины имеет особенность тина у³ = х⁴, а проектирование - тип 6.

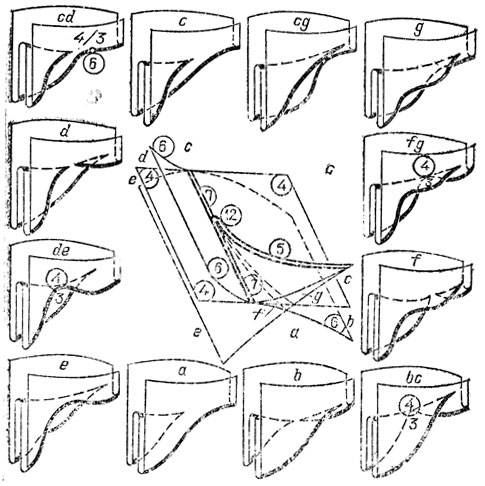
Рис. 68. Бифуркации проектирований: случай 12, z = х⁴ + х²у + ху³

Остальные особенности возникают при проектировании по направлению, асимптотическому в параболической точке. Простейшие из них - особенности 3 и 4. Проектирование 3 реализуется в момент, когда мы, спускаясь с бугра, начинаем видеть его контур (см. рис. 41). Первая появляющаяся точка контура - параболическая.

При прохождении особенности 4 происходит слияние или разделение двух компонент видимого контура.

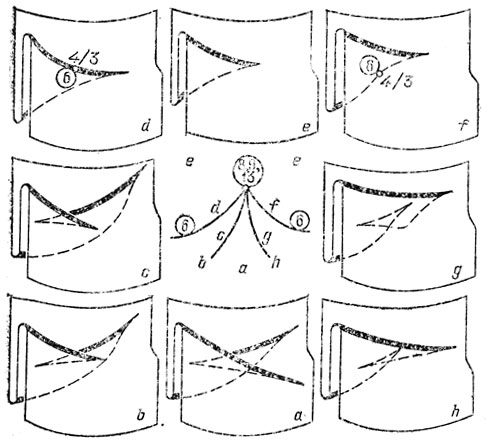
Рис. 69. Бифуркации проектирований: случай 13, z = х⁵ + ху

Особенности 5, 7, 8 и 9 реализуются лишь при изолированных направлениях проектирования, и их нужно специально искать. (8 и 9 - проектирование вдоль касательной четвертого порядка, 7 - вдоль параболической касательной третьего порядка, 5 - точка "параллельности асимптотических в бесконечно близких параболических точках"). При проектированиях из отдельных точек реализуются еще 4 особенности 10 - 13: z = х³ ± ху⁴, z = х⁴ + х²у + ху³, z = х⁵ + ху (рис. 66 - 69).