11. Особенности границы достижимости

Управляемая система в фазовом пространстве задается так: в каждой точке пространства дан не один вектор скорости (как в обычной эволюционной системе), а целее множество векторов, называемое индикатрисой допустимых скоростей (рис. 54).

Задача управления состоит в том, чтобы, выбирая в каждый момент времени вектор скорости из предосталяемого индикатрисой набора допустимых скоростей, достичь заданной цели (например, прийти за кратчайшее время на заданное подмножество фазового пространства).

Зависимость кратчайшего времени достижения цели от начальной точки может иметь особенности. Рассматривавшиеся в н. 10 особенности функции минимума расстояния до кривой - частный случай (индикатриса - окружность, а цель - кривая). В отличие от этого частного случая особенности кратчайшего времени в общей задаче управления изучены весьма слабо.

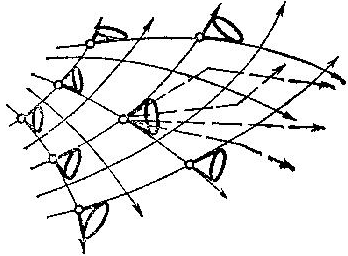
Рис. 54. Поле индикатрис допустимых скоростей управляемой системы

В общем случае достичь цели можно не при любом начальном условии. Точки фазового пространству из которых можно достичь цели (за любое время), называются областью достижимости.

Граница области достижимости может иметь особенности даже в том случае, когда пи цель, ни поле индикатрис в различных точках фазового пространства особенностей не имеют. Мы приводим ниже классификацию особенностей границы достижимости в общей управляемой системе па фазовой плоскости в случае, когда индикатрисы и цель - гладкие кривые (по А. А. Давыдову).

Из четырех типов особенностей границы три записываются простыми формулами (при подходящем выборе локальных координат на плоскости):

Особенность четвертого тина связана с теорией дифференциальных уравнений, неразрешенных относительно производной, называемых также неявными дифференциальными уравнениями.

Такое уравнение имеет вид F(х, у, р) = 0, где р = dy/dx. Геометрически уравнение F = 0 задает поверхность в трехмерном пространстве с координатами (х, у, р). Она называется поверхностью уравнения.

Условие р = dy/dx выделяет плоскость в каждой точке нашего трехмерного пространства. Эта плоскость состоит из векторов, у-компонента которых в р раз больше х-компоненты, где р - координата точки приложения. Такая плоскость называется контактной. Контактная плоскость в каждой точке вертикальна (содержит направление оси р). Все вместе контактные плоскости задают поле контактных плоскостей, называемое также контактной структурой.

Контактная структура высекает на поверхности уравнения поле направлений (с особыми точками в тех местах, где контактная плоскость касается поверхности). Поверхность уравнения здесь предполагается гладкой. Это условие выполняется для уравнений общего положения.

Вопрос о строении типичных особых точек неявных дифференциальных уравнений рассматривался еще в прошлом веке, и король Швеции Оскар II включил его, наряду с проблемой трех тел, а список из четырех вопросов на премию 1885 г.

Решение этого вопроса было получено лишь в 1985 г. А. А. Давыдовым в виде побочного продукта исследования областей достижимости управляемых систем па плоскости.

Ответ доставляет следующий список нормальных форм (к которым уравнение приводится локальным диффеоморфизмом плоскости):

В зависимости от значения параметра к здесь возможны три случая. Особая точка поля на поверхности уравнения может оказаться седлом, узлом или фокусом. Отображение проектирования поверхности уравнения на плоскость (х, у) вдоль оси р имеет особенностью складку. В окрестности типичной точки складки уравнение приводится к нормальной форме Чибрарио (1932), х = р². Все особые точки автоматически попадают на складку. Результат складывания изображен на рис. 55: особые точки па плоскости (х, у) называются сложенным седлом (узлом, фокусом соответственно). Оказывается, несмотря па сложность узора, образованного интегральными кривыми па плоскости (х, у), он (даже не только топологически, но и с точностью до диффеоморфизма) однозначно определяется единственным "модулем" k (как и фазовый портрет соответствующего векторного поля на плоскости вблизи особой точки).

Сложенные особые точки - седла, узлы, фокусы - встречаются во многих приложениях. Рассмотрим, например, асимптотические линии на поверхности в трехмерном пространство (поверхность имеет с касательными прямыми касание выше первого порядка в каждой своей точке). Для поверхности общего положения сеть асимптотических линий заполняет область гиперболичности, где поверхность имеет отрицательную кривизну (как обыкновенное седло). Через каждую точку области гиперболичности проходят две асимптотические лини и область гиперболичности ограничена линией параболических точек, на которой оба асимптотических направления совпадают.

В окрестности типичной параболической точки асимптотические линии имеют полу кубическую особенность и вся сеть их приводится к такой же нормальной форме у = с ± х^3/2 как и семейство интегральных кривых уравнения Чибрарио.

Однако в окрестности отдельных точек на линии параболичности поведение асимптотических линий сложнее: они устроены как интегральные кривые неявных уравнений вблизи сложенных особых точек (рис. 55).

Сложенные особенности появляются также в теории релаксационных колебаний. Пусть система имеет одну быструю и две медленных переменных, так что полное фазовое пространство трехмерно. Точки, где скорость изменения быстрой переменной равна нулю, образуют (вообще говоря гладкую) поверхность - медленную поверхность системы. Движение фазовой точки состоит из нескольких процессов. Вначале быстрая переменная релаксирует, т. е. фазовая точка быстро движется по "вертикали" (по направлению оси быстрой переменной) к медленной поверхности затем начинается медленное движение вдоль прямыми касание выше первого порядка в каждой своей точке). Для поверхности общего положения сеть асимптотических линий заполняет область гиперболичности, где поверхность имеет отрицательную кривизну (как обыкновенное седло). Через каждую точку области гиперболичности проходят две асимптотические линии. Область гиперболичности ограничена линией параболических точек, на которой оба асимптотических направления совпадают.

В окрестности типичной параболической точки асимптотические линии имеют полукубическую особенность и вся сеть их приводится к такой же нормальной форме у = с ± х^3/2, как и семейство интегральных кривых уравнения Чибрарио.

Однако в окрестности отдельных точек на линии параболичности поведение асимптотических линий сложнее: они устроены как интегральные кривые неявных уравнений вблизи сложенных особых точек (рис. 55).

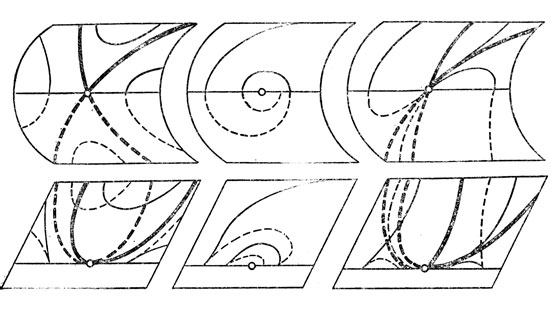
Рис. 55. Сложенные особенности

Сложенные особенности появляются также в теории релаксационных колебаний. Пусть система имеет одну быструю и две медленных переменных, так что полное фазовое пространство трехмерно. Точки, где скорость изменения быстрой переменной равна нулю, образуют (вообще говоря гладкую) поверхность - медленную поверхность системы. Движение фазовой точки состоит из нескольких процессов. Вначале быстрая переменная релаксирует, т. е. фазовая точка быстро движется по "вертикали" (по направлению оси быстрой переменной) к медленной поверхности, затем начинается медленное движение вдоль этой поверхности. Траектории этого движения определяются полем направлений, высекаемым на ней полем плоскостей, натянутых на вертикальное направление (направление оси быстрой переменной) и направление возмущений. Это поле плоскостей определяет, вообще говоря, контактную структуру в фазовом пространстве, и особенности медленного движения описываются, вообще говоря, сложенными особыми точками рис. 55.

В качестве последнего примера тех же особенностей рассмотрим движение материальной точки в потенциальной яме (или у потенциального барьера) в присутствии трения. Обозначим (рис. 56) через х координату точки, а через Е ее полную энергию. Проекции фазовой траектории на плоскость (х, Е) имеют при подходе к графику потенциальной энергии полукубические, вообще говоря, особенности. Минимуму (максимуму) потенциальной энергии отвечает особая точка. Для потенциальной энергии общего положения получаются все те же сложенные особенности Давыдова.

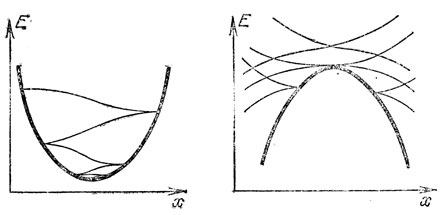
Рис. 56. Диссипация энергии в яме и у барьера

Причина, по которой сложенные особенности встречаются столь часто, состоит в том, что часто встречаются как обычные особенности векторного поля, так и складывания. Неожиданным здесь является лишь то, что комбинирование складывания с особенностью не приводит к большему разнообразию случаев, чем в классификации самих особенностей векторных полей. А именно, рассмотрим складывание как инволюцию (диффеоморфизм, квадрат которого - тождественное преобразование) на плоскости, несущей векторное поле с особой точкой. Если линия неподвижных точек инволюции проходит через особую точку поля и инволюция на этой линии меняет знак каждого вектора поля на противоположный, то такая инволюция (почти всегда) переводится в любую другую инволюцию с такими свойствами при помощи диффеоморфизма, двигающего вдоль себя каждую фазовую кривую заданного поля. Этот (довольно неожиданный) результат является источником всей описанной выше теории.

Четвертая особенность границы достижимости получается из двух сепаратрис сложенных седел, входящих с разных сторон в сложенный узел. Приведенная выше нормальная форма сложенного узла позволяет явно выписать нормальную форму четвертой особенности, но я здесь не буду этого делать.

Примеры управляемых систем и целей, приводящих к указанным особенностям границы достижимости, изображены на рис. 57, 58, 59. На этих рисунках цель у обозначена двойной линией, граница области достижимости - Т-образным пунктиром (ножка буквы Т обращена в сторону области достижимости). Линии со стрелками касаются краев конусов допустимых направлений в каждой точке; горизонтально заштрихована область "полной управляемости, (выпуклая оболочка индикатрисы окружает 0). Рассматривая рис. 57 - 59 читатель может проверить неустранимость особенностей 1 - 4.

Чтобы разобраться в этих рисунках, мы построим сеть предельных линий, определяемую следующим образом.

В каждой точке вне области полной управляемости направления допустимых скоростей расположены внутри угла, меньшего 180°.

Стороны этого угла определяют направления предельных скоростей в данной точке. Таким образом, в каждой точке вне области полной управляемости возникают два предельных направления. Интегральные кривые нолей предельных направлений (т. е. кривые, имеющие предельное направление в каждой своей точке) называются предельными линиями.

Сеть предельных линий изображена на рис. 54 вместе с индикатрисами допустимых скоростей (они имеют вид эллипсов) и с опирающимися на индикатрисы углами, образованными допустимыми направлениями движения.

Граница области достижимости состоит из отрезков предельных линий (и, быть может, отрезков линии цели, если цель не лежит в области полной управляемости, см. рис. 57). Эти отрезки соединяются между собой в точках, которые и составляют особенности границы области достижимости.

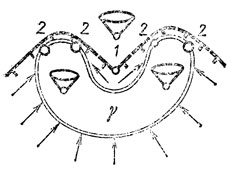
Рис. 57. Устойчивость особенностей 1 и 2 на границе области достижимости

На рис. 57 цель имеет вид контура лежащей на спине буквы С. допустимые скорости во всех точках плоскости одинаковы и надавлены вверх под углом, составляющим не более 45° с вертикалью.

Наклон всех предельных линий ±45°. Граница достижимости обозначена Т-образным пунктиром. Видны особые точки границы двух типов: 1 и 2.

В точке 1 соединяются отрезка двух разных предельных линий. Они пересекаются под ненулевым углом. Ясно, что из точек, расположенных выше указанной на рис. 57 границы, при движении по направлению, образующему с вертикалью угол 45° или меньше, попасть на цель нельзя, а из точек, расположенных ниже, - можно. Интересно отметить, что вершина 1 зияет на границе области достижимости: область недостижимости вклинивается в этом месте в области достижимости. Таким образом, в смысле п. 7 хороший оказывается именно недостижимое.

В точке 2 на границе достижимости соединяется отрезок предельной линии и отрезок линии-цели. В этой точке направление линии-цели предельное, так что граница достижимости имеет касательную. Кривизна границы, однако, меняется в точке 2 скачком при переходе с предельной линии на линию-цель.

Заменим теперь цель на рис. 57 любой близкой гладкой кривой (близость кривых предполагает близость их касательных, кривизн и т. д.) и заменим поле индикатрис допустимых скоростей на рис. 57 близким полем. Тогда ясно, что граница допустимости новой системы по-прежнему будет иметь вблизи точки 1 точку излома (где под ненулевым углом соединяются отрезки двух предельных линий). Точно так же вблизи каждой из точек 2 возникает точка аналогичного характера для новой системы.

Таким образом, ситуация, изображенная на рис. 57, устойчива относительно малых шевелений системы. Подобным свойством устойчивости обладают и ситуации, изображенные на рис. 58 и 59. События, приводящие к указанным на этих рисунках особенностям сети предельных линий, состоят в следующем.

На рис. 58 кривая К ограничивает заштрихованную область полной управляемости: в заштрихованной области движение в любом направлении возможно (если допускать так называемые смешанные стратегии, т. е. движения быстро сменяющимися галсами). Цель на рис. 58 лежит в области полной управляемости. Следовательно, вся ограниченная кривой К область достижима.

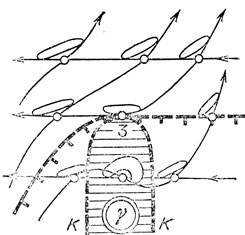
Рис. 58. Устойчивость особенности 3 на границе области достижимости

На границе К области полной управляемости угол между допустимыми направлениями составляет ровно 180°. Граница К образована теми точками плоскости, для которых двойная касательная, делающая выпуклой индикатрису допустимых скоростей, проходит через начало координат плоскости скоростей (двойная касательная - это прямая, касающаяся кривой в двух точках).

На рис. 58 эта двойная касательная в каждой точке кривой К горизонтальна. Событие, приводящее к образованию изображенной на рис. 58 особенности, состоит в том, что кривая К сама касается проходящей через пуль двойной касательной к индикатрисе.

Для систем общего положения такое событие происходит лишь в отдельных точках границы К области полной управляемости. На рис. 58 оно происходит в точке 3, где касательная к К горизонтальна.

Из сказанного выше ясно, что описанное событие реализуется устойчивым образом: при малом шевелении системы, т. е. цели и поля индикатрис допустимых скоростей, точка 3 несколько сместится, но не исчезнет.

Рассмотрим теперь сеть предельных линий вблизи точки 3. Оба поля предельных направлений вблизи нее гладкие. Выбором соответствующей системы координат одно из них можно выпрямить. На рис. 58 система координат так и выбрана: первое из двух семейств предельных линий состоит из горизонтальных прямых (направленных влево).

Линии второго семейства - гладкие кривые. На кривой К они касаются линий первого семейства. В интересующей нас точке 3 оба семейства касаются линии К. Из этих соображений уже нетрудно усмотреть, что сеть предельных линий вблизи точки 3 выглядит так, как указано на рис. 58: выше кривой К линии второго семейства поднимаются при движении вдоль допустимого направления, ниже - опускаются (выбор направлений линий сети допускает еще несколько вариантов, аналогичных изображенному; разобравшись в рис. 58, читатель легко разберется в них сам).

Теперь на рис. 58 видно, что левее точки 3 граница области достижимости идет по линии второго предельного направления, а правее - первого (горизонтального). В точке 3 обе линии имеют второй порядок касания (как прямая и кубическая парабола). В окрестности этой точки граница достижимости диффеоморфна^* графику функции у = х² | х |.

^*(Диффеоморфизм - это замена координат, гладкая вместе с обратной заменой.)

Таким образом, точки 1 и 2 на рис. 57 и точка 3 на рис. 58 дают примеры устойчиво реализуемых событий на границе области достиэжимости, вызывающих особенности первых трех видов с. 49. Особенности четвертого вида возникают в ситуации рис. 59.

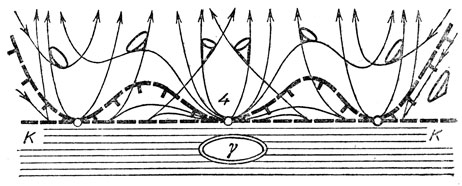
Рис. 59. Сложенные особенности на границе области достижимости

На этом рисунке, как и на рис. 58, цель находится внутри заштрихованной области полной управляемости. На границе К этой области расположены точки плоскости, в которых выпуклая индикатриса проходит через нуль. Ясно, что в управляемых системах общего положения это явление - прохождение индикатрисы через 0 - реализуется на линии. По одну сторону этой линии К лежит область полной управляемости (индикатриса окружает 0), по другую - область с двумя предельными направлениями. На разделяющей их границе К оба эти поля направлений сливаются в одно - поле направлений касательных к индикатрисам в нуле.

В общей точке кривой К направление этого поля составляет с К ненулевой угол. Событие, приводящее к особенности четвертого типа на границе области достижимости, - это касание кривой К с предельным направлением. Для систем общего положения такое касание реализуется в отдельных точках границы области полной управляемости К. На рис. 59 таких точек на кривой К три; средняя из них обозначена цифрой 4.

Чтобы изучить сеть предельных линий в окрестностях этих особых точек, полезно рассмотреть наше двузначное поле предельных направлений как однозначное поле направлений на поверхности, двулистно накрывающей область выше кривой К.

С этой целью рассмотрим множество всех направлений линейных элементов на плоскости. Это множество является трехмерным многообразием, так как направление определяется точкой приложения линейного элемента (две координаты) и еще своим азимутом (одна угловая координата).

Множество всех предельных направлений составляет подмножество множества всех направлений. Это подмножество - гладкая поверхность в трехмерном многообразии всех направлений. Трехмерное многообразие всех направлений проектируется на исходную плоскость (линейный элемент проектируется в свою точку приложения). Поверхность, образованная предельными направлениями, проектируется при этом в часть плоскости, расположенную выше кривой К. Это отображение проектирования поверхности на плоскость над кривой К имеет особенность, а именно складку Уитни.

Двузначное поле предельных направлений на плоскости определяет на построенной поверхности однозначное поле направлений всюду, кроме тех самых особенных точек кривой К (где индикатриса в 0 касается К), которые мы хотим изучать.

Предельные линии обоих полей предельных направлений после перехода на построенную поверхность образуют систему фазовых кривых гладкого векторного поля с особенностями в интересующих нас точках. Эти особые точки могут быть узлами, фокусами или седлами (на рис. 59 средняя точка - узел, а обе крайние - седла). Таким образом, расположение предельных линий на исходной плоскости получается из расположения фазовых кривых векторного поля в окрестности особой точки при отображении складки Уитни. Хотя это отображение Уитни и фазовые кривые не вполне независимы (в частности, над К фазовые кривые касаются ядра проектирования), сказанного достаточно, чтобы исследовать расположение предельных линий вблизи особой точки (между прочим, такую же картину образуют асимптотические линии вблизи параболической кривой на поверхности).

На рис. 59 изображен один из вариантов этого расположения. На рисунке видно, что изображенная Т-образным пунктиром граница области достижимости образована проекциями сепаратрис седел (крайних особых точек) при отображении двулистно накрывающей поверхности на плоскость. Над точкой 4 на накрывающей лежит особая точка типа "узел". В этот узел входят с разных сторон две сепаратрисы седел.

В узле эти две кривые имеют общую касательную и (в случав общего положения) могут быть заданы уравнениями парабол степени α > 1 вида

в подходящей системе координат.

Четвертая особенность границы области достижимости получается из этой пары парабол степени α на накрывающей поверхности при отображении складки Уитни.

Это обстоятельство показывает, между прочим, ошибочность чрезвычайно распространенного среди катастрофистов вульгарного истолкования деклараций Р. Тома о том, что "в природе встречаются только устойчивые явления и потому при изучении каждой задачи следует изучать устойчивые случаи, отбрасывая остальные как нереализуемые". В данном случае особенности первых трех типов устойчивы (с точностью до диффеоморфизмов), а четвертого нет. В то же время все 4 типа особенностей встречаются одинаково часто и изучение последней ничуть не менее важно, чем исследование остальных трех.

Об особенностях области достижимости, функции времени и оптимальной стратегии в управляемых системах общего положения с фазовым пространством большей размерности известно удивительно мало - лишь в 1982 г. доказано, что область достижимости является топологическим многообразием с краем.

Одним из промежуточных вопросов при исследовании управляемых систем оказывается вопрос об особенностях выпуклых оболочек гладких многообразий (кривых, поверхностей,...).

Выпуклой оболочкой множества называется пересечение всех содержащих его полупространств. Индикатриса управляемой системы может быть невыпуклой.

Однако оказывается, что невыпуклую индикатрису можно заменить ее выпуклой оболочкой.

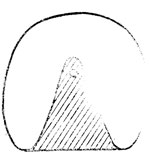
Рис. 60. Овыкупление индикатрисы при помощи смешанной стратегии

Например, индикатриса скоростей яхты при встречном ветре невыпукла (рис. 60). Против ветра можно, однако, двигаться галсами, применяя смешанную стратегию, т. е. перемежая участки движения с разными скоростями, принадлежащими индикатрисе. Средняя скорость движения при смешанной стратегии принадлежит множеству средних арифметических используемых векторов индикатрисы, т. е. выпуклой оболочке.

Особенности выпуклых оболочек кривых и поверхностей общего положения в трехмерном пространстве исследованы В. Д. Седых и В. М. Закалюкиным. В случае кривых с точностью до гладкой замены переменных оболочка задается в окрестности каждой своей точки одной из шести формул:

(рис. 61). В случае поверхностей - одной из трех формул

где ρ (х, у) - расстояние от точки (х, у) до угла у ≥ с | х | (рис. 62). Число с > 0 является модулем (инвариантом): оболочки, соответствующие разным с, не сводятся одна к другой гладким преобразованием.

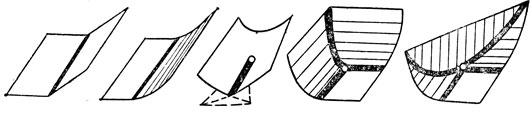
Рис. 61. Типичные особенности выпуклых оболочек пространственных кривых

Особенности выпуклых оболочек в пространстве большей размерности мало изучены. Согласно В. Д. Седых, выпуклая оболочка общего k-мерного многообразия в пространстве размерности выше к+2 имеет модули, являющиеся функциями к переменных.

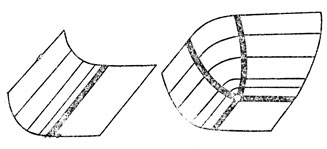
Рис. 62. Типичные особенности выпуклых оболочек поверхностей

Тень, отбрасываемая бесконечно-гладким или даже аналитическим выпуклым телом, может, как это ни кажется странным, иметь особенности. А именно, граница тени трехмерного выпуклого тела может иметь разрывы третьей производной, а тела размерности 4 и выше - даже второй (И. А. Богаевский, 1990).

Много новых интересных особенностей возникает в оптимизационных задачах с ограничениями, например в задаче об обходе препятствия. Их исследование привело к новым результатам в одной из самых классических областей математики - геометрии гладких поверхностей в трехмерном пространстве.