10. Особенности в задачах оптимизации: функция максимума

Многочисленные особенности, бифуркации и катастрофы (скачки) возникают во всех задачах о нахождении экстремумов (максимумов, минимумов), задачах оптимизации, управления и принятия решений. Представим себе, например, что мы должны выбрать х так, чтобы обеспечить наибольшее значение функции f (х) (рис. 50). При плавном изменении функции оптимальное решение меняется скачком, перескакивая с одного из двух конкурирующих максимумов (Л) на другой (В).

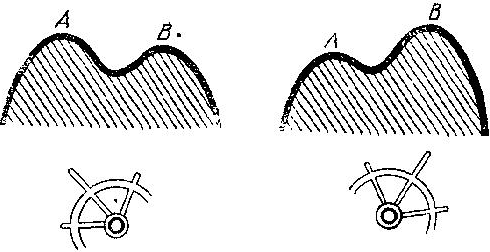
Рис. 50. Разрыв оптимального управления

Ниже мы рассмотрим несколько задач такого рода; все они далеки от полного решения, хотя в некоторых классификация особенностей проведена достаточно далеко.

Рассмотрим семейство f(х, у) функций переменной х, зависящих от параметра у. При каждом фиксированном значении параметра у вычислим максимум функции, обозначим его через

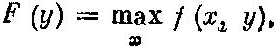
Функция F непрерывна, но не обязательно гладкая, даже если f - многочлен.

Пример 1. Пусть у - азимут луча зрения, х - дальность, f - угловая высота ландшафта на расстоянии х при азимуте у (рис. 51). Тогда F определяет линию горизонта. Ясно, что линия горизонта гладкой поверхности может иметь изломы и они неустранимы малым шевелением.

Рис. 51. Излом линии горизонта гладкого ландшафта

Переменная х и параметр у могут быть точками пространств любой размерности; наряду с максимумами встречаются и минимумы.

Пример 2. Пусть х - точка плоской кривой у" у - точка области, ограниченной этой кривой, f(х, у) - расстояние от у до х.

Будем рассматривать f как функцию точки кривой, зависящую от точки области как от параметра. Тогда функция минимума семейства, F(у), есть кратчайшее расстояние от точки у до кривой у (рис. 52). Ясно, что эта функция непрерывна, но не всюду гладкая.

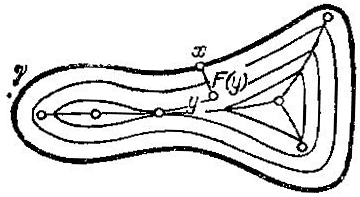
Рис. 52. Расстояние до кривой и его особые точки

Мы можем представить себе лопату, ограниченную кривой γ; насыпем на эту лопату возможно большую кучу сухого песка. Поверхность кучи будет тогда графиком функции F. Ясно, что для лопаты общего положения поверхность кучи имеет хребет (линию излома).

Линии уровня функции F - не что иное, как передние фронты распространяющегося внутрь кривой γ возмущения.

Теория особенностей позволяет перечислить особенности функций максимума F как в описанном примере, так и для семейств общего положения функций любого числа переменных при условии, что число параметров у не больше 10 (Л. Н, Брызгалова). Рассмотрим простейшие случаи одного и двух параметров.?

Выбирая координаты на оси (плоскости) значений параметра у и вычитая из F гладкую функцию параметров, мы можем привести функцию максимума семейства общего положения в окрестности каждой точки к одной из следующих нормальных форм:

один параметр:

два параметра:

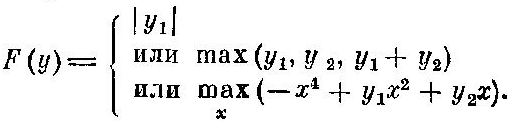
Формула, относящаяся к случаю одного параметра означает, в частности, что линия горизонта гладкого ландшафта общего положения не имеет особенностей, отличных от простейших изломов. Особенности функции максимума, описанные формулами для двух параметров, дают следующие особенности функции минимума (например, особенности поверхности кучи песка на лопате): линия хребта, точка соединения трех хребтов и конец хребта (см. рис. 52).

В последнем случае график функции минимума есть часть поверхности ласточкиного хвоста (см. рис. 34), получающаяся удаленном прилежащей к ребру возврата пирамиды (ВСВ) (и еще отражением поверхности рис. 34 в горизонтальной плоскости).

При 3, 4, 5 и 6 параметрах число различных особенностей равно соответственно 5, 8, 12 и 17; начиная с 7 параметров, число типов несводимых друг к другу особенностей становится бесконечным: нормальные формы неизбежно содержат "модули", являющиеся функциями от параметров.

Топологически функция максимума (минимума) семейства общего положения устроена как гладкая функция общего положения (В. И. Матов).

На рис. 53 изображены типичные особенности множества негладкости функции максимума трехпараметрического семейства.

Они позволяют исследовать типичные перестройки особенностей ударных волн на плоскости, происходящие с течением времени: для этого нужно сперва изучить типичные перестройки двумерных сечений пяти изображенных на рис. 53 поверхностей (эти перестройки также изображены на рисунке), Оказывается, некоторые из них являются, а некоторые не являются перестройками ударных волн (например, для потенциальных решений уравнения Бюргерса u_t + uu_х = εu_хх с исчезающей вязкостью ε).

А именно, реализуются ударными волнами те перестройки, которые отмечены на рис. 53 стрелками. Правила отбора найдены И. А. Богаевским и Ю. М. Барышниковым:

1) возникающая после перестройки ударная волна в окрестности точки перестройки стягиваема;

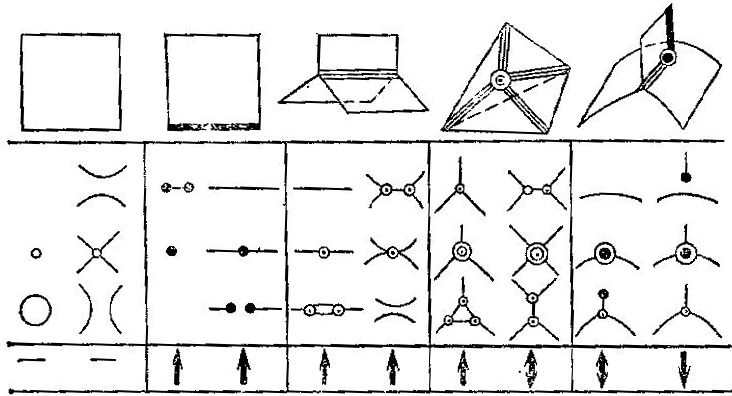
Рис. 53. Типичные особенности множества во гладкости максимума и типичные перестройки ударных волн

2) дополнение к ударной волне в момент перестройки и сразу после нее топологически (гомотопически) одинаковы.

Каждое из этих условий необходимо и достаточно для реализуемости типичной перестройкой ударных волн на плоскости и в трехмерном пространстве типичной перестройки. особенностей функции максимума. Так ли это в многомерном случае - неизвестно.