9. Крупномасштабное распределение вещества во вселенной

В настоящее время распределение вещества во Вселенной крайне неоднородно (существуют планеты. Солнце, звезды, галактики, скопления галактик и т. д.). Современная астрофизика считает, что на ранних этапах развития Вселенной таких неоднородностей не было. Как же они образовались? Я. Б. Зельдович в 1970 г. предложил объяснение образования скоплений пылевидной материи, математически эквивалентное анализу возникновения особенностей каустик, начатому в 1963 г. Е. М. Лифшицем, Халатниковым и Судаковым.

Рассмотрим бесстолкновительную среду, т. е. среду настолько разреженную, что ее частицы проходят друг "сквозь" друга, не сталкиваясь. Предположим, для простоты, что частицы не взаимодействуют и движутся по инерции: через время t частица, находившаяся в точке х, перейдет в точку х + vt.

Предположим, что в начальный момент скорость частицы, находящейся в точке х, была v₀ (х); векторное поле v₀ называется начальным полем скоростей среды. С течением времени частицы будут двигаться и поле скоростей будет меняться (хотя скорость каждой частицы и не меняется, в следующий момент времени эта частица находится на новом месте).

На рис. 47 изображено начальное поле скоростей одномерной среды v₀ и получающиеся аз него через время t = 1, 2 и 3 ноля v₁, v₂, v₃. Мы видим, что, начиная с некоторого момента, более быстрые частицы начинают обгонять более медленные; в результате поле скоростей становится трехзначным: через одну точку пространства проходят с разными скоростями три потока частиц.

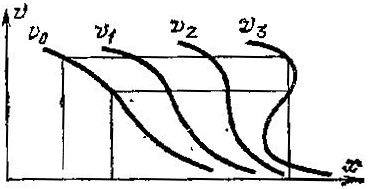
Рис. 47. Эволюция поля скоростей бесстолкновительной среды

Движение нашей среды можно описать как однопараметрическое семейство отображений прямой на прямую. Именно для каждого t определено отображение g_t, переводящее начальное положение частицы (х) в конечное: g_t = х + v₀ (х)t.

Отображение g₀ есть тождественное преобразование, оставляющее каждую точку на месте. Отображения, соответствующие моментам t, близким к 0, взаимно однозначны и не имеют особенностей. После момента первого обгона отображение g_t имеет две складки.

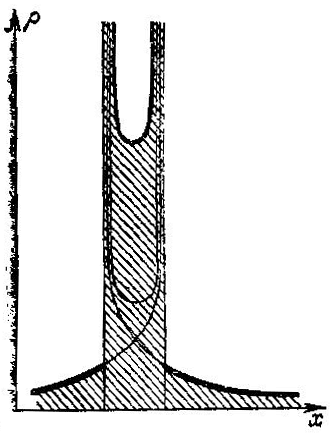
Рис. 48. Особенности плотности после обгона

Пусть в начальный момент плотность среды в точке х была ρ₀(х), С течением времени плотность будет меняться. Нетрудно сообразить, что после обгона график плотности будет иметь вид, изображенный па рис. 48 (на расстоянии 8 от точки складки плотность оказывается порядка 1/√ε).

Таким образом, небольшие отличия начального ноля скоростей от постоянного приводят через достаточно большое время к образованию скоплений частиц (в местах бесконечно большой плотности).

Этот вывод сохраняется при переходе от одномерной среды к среде, заполняющей пространство любой размерности, и при учете влияния на движение ее частиц внешнего силового поля или поля, созданного средой, а также при учете аффектов теории относительности и расширения Вселенной.

Если силовые поля потенциальны (т. е. их работа на любом пути зависит лишь от начала и конца пути) и начальное поле скоростей тоже потенциально, то задача описания особенностей отображений g_t и их метаморфоз при изменении t математически тождественна задаче об особенностях каустик и их метаморфоз (то и другое составляет предмет теории так называемых лагранжевых особенностей).

Точки бесконечной плотности образуют в случае двухмерной среды кривые на плоскости. Эти кривые образованы критическими значениями отображения g_t, т. е. его значениями в критических точках (для отображения рис. 1 критические точки - это точки экватора сферы, критические значения - точки видимого контура на горизонтальной плоскости).

Линия критических значений отображения g_t называется его каустикой. Ее можно определить как место пересечений бесконечно близких лучей (траекторий частиц), т. е. так же, как обычную оптическую каустику.

Таким же образом описание метаморфоз оптических каустик доставляет нам описание перестроек скоплений частиц (мест бесконечной плотности среды) при потенциальном движении.

Первая особенность на плоскости выглядит как серпик с полукубически заостренными вершинами (в трехмерном пространстве новорожденная каустика имеет вид блюдца). Я. Б. Зельдович назвал такую каустику блином (первоначально блины интерпретировались как галактики, позже - как скопления).

При дальнейшем движении среды рождаются новые блины. Кроме того, имеющиеся блины начинают перестраиваться и могут взаимодействовать друг с другом. Одна из типичных последовательностей событий в двухмерной среде изображена на рис. 49.

Все возможные в трехмерной среде элементарные перестройки изображены на рис. 44, 45 (получение этих результатов уже требует сложной математической теории лагранжевых особенностей).

В результате перестроек плотность имеет особенности различных порядков на поверхностях блинов, на линиях и в отдельных точках. Будем характеризовать особенность средней плотностью в ε-окрестности рассматриваемой точки (т. е. отношением массы, попавшей к ε-окрестность, к объему окрестности).

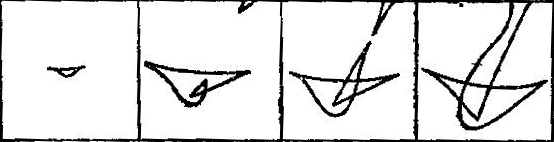
Рис. 49. Сценарий взаимодействия 'блинов' Зельдовича

В точках каустики средняя плотность стремится к бесконечности когда радиус окрестности ε стремится к пулю.

Порядок величины средней плотности в различных точках каустик таков:

При изменении времени в отдельные моменты появляются особенности А₅ со средней плотностью порядка ε^-1/5 и D₅ (ε^-1 и ε^-1).

Согласно астрофизикам, в те времена, когда радиус Вселенной был раз в тысячу меньше нынешнего, крупномасштабное распределение вещества во Вселенной было практически однородным, а поле скоростей - практически потенциальным. Дальнейшее движение частиц привело к образованию каустик, т. е, особенностей плотности и скоплений частиц. До образования блинов плотность остается достаточно малой, чтобы считать среду бесстолкновительной. После этого момента среду можно считать бесстолкновительной, если предполагать что значительная часть массы Вселенной сосредоточена в массивных нейтрино; если же большая часть массы приходится на протоны и нейтроны, то к выводам из геометрии каустик и их перестроек следует относиться с осторожностью, так как среда перестает быть бесстолкновительной.

Выводы о скоплении вещества на поверхностях с преимущественным скоплением вдоль некоторых линий (шнуров), соединяющихся в особых точках (узлах), по-видимому, соответствуют астрономическим наблюдениям, по крайней мере в общих чертах (С. Ф. Шандарин).