
8. Каустики, волновые фронты и их метаморфозы
Один из наиболее важных выводов теории особенностей состоит в универсальности нескольких простых образов вроде складки, сборки и точки возврата, которые должны встречаться повсеместно и которые полезно научиться распознавать. Кроме перечисленных особенностей, часто встречаются еще несколько образов, которые также получили собственные имена: "ласточкин хвост", "пирамида", "кошелек" и др.
Пусть в какой-либо среде распространяется некоторое возмущение (например, ударная волна, свет или эпидемия).
Для простоты начнем с плоского случая. Допустим, в начальный момент времени возмущение имелось на кривой а (рис. 32), и пусть скорость его распространения равна 1. Чтобы узнать, где будет возмущение через время t, нужно отложить по каждой нормали к кривой отрезок длины t. Получающаяся кривая называется волновым фронтом.
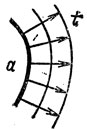
Рис. 32. Эволюция волнового фронта
Даже если начальный волновой фронт не имел особенностей, через некоторое время особенности начнут возникать. Например, при распространении возмущения внутрь эллипса, возникают особенности, изображенные на рис. 33. Эти особенности устойчивы (неустранимы малым шевелением начального фронта). Для гладкого начального фронта общего положения с течением времени будут образовываться лишь стандартные особенности такого же типа.
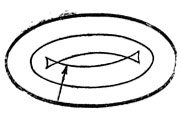
Рис. 33. Особенности эквидистант эллипса
Все иные особенности (например, особенность в центре сжимающейся окружности) при малом шевелении начального фронта рассыпаются на несколько особенностей стандартного вида.
В трехмерном пространстве на гладком волновом фронте общего положения с течением времени возникают лишь ребра возврата и стандартные особенности типа "ласточкин хвост", изображенные на рис. 34 (попытайтесь разобраться в особенностях фронта, распространяющегося внутрь трехосного эллипсоида).
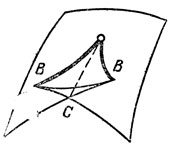
Рис. 34. Ласточкин хвост
Все более сложные особенности при малом шевелении фронта рассыпаются на соединенные ребрами возврата и линиями самопересечения ласточкины хвосты.
Ласточкин хвост можно определить как множество всех точек (а, b, с), таких, что многочлен х3 + ах2 + bх + с имеет кратный корень. У этой поверхности есть ребро возврата (В на рис. 34) и линия самопересечения (С на рис. 34).
Ласточкин хвост можно получить из пространственной кривой А = t2, В = t3, С = t4: он образован всеми ее касательными.
Рассмотрим пересечения ласточкиного хвоста параллельными плоскостями общего положения (см. рис. 35).
Эти пересечения являются плоскими кривыми, При поступательном движении плоскости указанные кривые перестраиваются в момент, когда плоскость проходит через вершину хвоста. Перестройка (метаморфоза), происходящая при этом, в точности такая же, как метаморфоза волнового фронта на плоскости (например, при распространении возмущения внутрь эллипса).
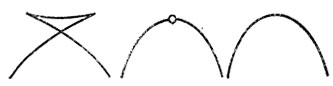
Рис. 35. Типичная перестройка волнового фронта на плоскости
Мы можем описать метаморфозы волновых фронтов на плоскости следующим образом. Рассмотрим наряду с основным пространством (в данном случае плоскостью) еще пространство-время (в данном случае трехмерное). Распространяющийся на плоскости волновой фронт заметает в пространстве-времени некоторую поверхность. Оказывается, саму эту поверхность всегда можно рассматривать как волновой фронт в пространстве-времени ("большой фронт"). В случае общего положения особенностями большого фронта будут ласточкины хвосты, ребра возврата и самопересечения, расположенные в пространстве-времени общим образом относительно изохрон (образованных "одновременными" точками пространства-времени). Теперь уже нетрудно сообразить, какие метаморфозы могут испытывать мгновенные волновые фронты на плоскости в случае общего положения; это перестройки сечений большого фронта изохронами.
Изучение метаморфоз волнового фронта при его распространении в трехмерном пространстве сводится таким же образом к исследованию сечений большого (трехмерного) волнового фронта в четырехмерном пространстве-времени трехмерными изохронами, Возникающие метаморфозы изображены на рис. 36.
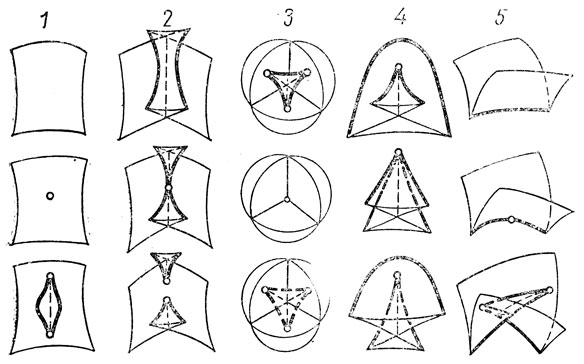
Рис. 36. Типичные перестройки волновых фронтов в трехмерном пространстве
Изучение метаморфоз волновых фронтов было одной из задач, из которых возникла теория катастроф, однако даже в случае трехмерного пространства катастрофисты не сумели с ней справиться; рис. 36 появился лишь в 1974 г., когда в теории особенностей были разработаны новые методы (основанные на теории кристаллографических групп симметрий).
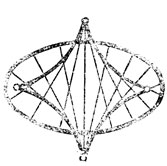
Рис. 37. Каустика эллипса
Наряду с волновыми фронтами процесс распространения возмущений описывается при помощи систем лучей. Например, распространение возмущений внутрь эллипса можно описать при помощи семейства внутренних нормалей к эллипсу (рис. 37). Это семейство имеет огибающую. Огибающая семейства лучей называется каустикой (т. е. "жгущей", так как в этих местах свет концентрируется), Каустика хорошо видна на внутренней поверхности чашки, освещенной солнцем. Радуга на небе также объясняется каустикой системы лучей, прошедших с полным внутренним отражением через каплю воды (рис. 38).
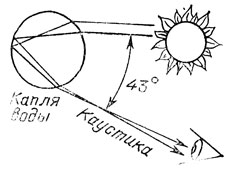
Рис. 38. Теория радуги Декарта
Каустика эллиптического фронта имеет четыре точки возврата. Эти особенности устойчивы: близкий к эллипсу фронт определит каустику с такими же особенностями. Все более сложные особенности каустик при малом шевелении рассыпаются на стандартные особенности: точки возврата (локальное уравнение - х2 = у3) и точки самопересечения.
Система нормалей к поверхности в трехмерном пространстве также имеет каустику. Эту каустику можно построить, отложив на каждой нормали к поверхности радиус кривизны (поверхность, вообще говоря, имеет в каждой точке два различных радиуса кривизны, так что на нормали получается две точки каустики).
Нелегко представить себе, как выглядят каустики даже простейших поверхностей, например трехосного эллипсоида.
Каустики общего положения в трехмерном пространстве имеют лишь стандартные особенности. Эти особенности называются "ласточкин хвост", "пирамида" и "кошелек" (см. рис. 39). Пирамида имеет три ребра возврата, касающиеся в вершине. Кошелек имеет одно ребро возврата и состоит из двух симметричных носов лодки, пересекающихся по двум линиям. Эти особенности устойчивы.
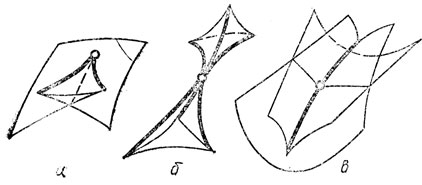
Рис. 39. Типичные особенности каустик в трехмерном пространстве
Все более сложные особенности каустик в трехмерном пространстве при малом шевелении рассыпаются на эти стандартные элементы.
Рассмотрим для одного и того же начального фронта (например, эллипса на плоскости) его каустику и фронты распространяющегося возмущения. Нетрудно понять, что особенности распространяющегося фронта скользят по каустике и заполняют ее.
Например, метаморфоза волнового фронта 5 на рис. 36 соответствует ласточкину хвосту на каустике. Ребро возврата движущегося в трехмерном пространстве волнового фронта заметает поверхность каустики (ласточкин хвост). Однако это разбиение каустики на кривые - не то разбиение поверхности ласточкиного хвоста на плоские кривые, с которым мы встречались выше (на рис. 35). Ребро возврата движущегося фронта не имеет самопересечений. Через точку линии самопересечения каустики ребро возврата движущегося фронта проходит два раза. Интервал времени между этими прохождениями очень мал (порядка ε5/2, где ε - расстояние от вершины хвоста).
Точно так же при перестройках 3 и 4 (см. рис. 36) ребра возврата движущихся фронтов заметают пирамиду и кошелек.
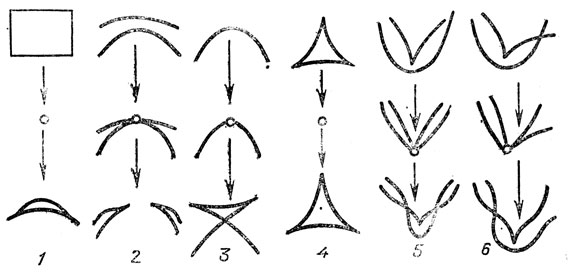
Рис. 40. Типичные перестройки каустик на плоскости
Если исходный фронт движется (зависит от параметра), то его каустика также движется и при своем движении способна испытывать метаморфозы. Метаморфозы движущихся каустик на плоскости можно изучить, рассматривая сечения большой каустики в пространстве-времени, подобно тому, как мы это делали для фронтов. Полученные метаморфозы изображены на рис. 40. (Это метаморфозы плоских сечений ласточкиного хвоста, кошелька и пирамиды.) Все более сложные метаморфозы рассыпаются на последовательности перечисленных при малом шевелении однопараметрического семейства.
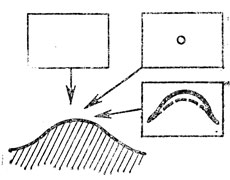
Рис. 41. Перестройка 'губы': рождение видимого контура
Обратим внимание па метаморфозу 1 рождения каустики "из воздуха", Новорожденная каустика имеет вид серпика с полукубическими остриями на концах ("губы", но терминологии Р. Тома). Аналогичным образом рождается "из воздуха" видимый контур поверхности при изменении направления проектирования (рис. 41), Глядя на бугор сверху, мы не видим контура. Когда луч зрения наклоняется, появляется вначале точечная особенность, которая затем быстро растет (пропорционально √t - t0, где t0 - момент появления особенности) и имеет вид "губ". Описанную здесь перестройку можно реализовать как перестройку плоского сечения поверхности с ребром возврата при поступательном движении плоскости (в момент перестройки плоскость касается ребра возврата (рис. 42)).
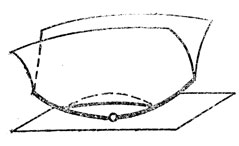
Рис. 42. Перестройка плоского сечения поверхности с ребром возврата
Метаморфозу 3 также можно увидеть на видимом контуре, для этого достаточно посмотреть на двугорбого верблюда, проходя мимо него (рис. 43). В момент метаморфозы профиль имеет такую же особенность, как кривая у3 = х4.

Рис. 43. Перестройка 'верблюд'
Все перестройки видимых контуров поверхностей в общих однопараметрических семействах исчерпываются первыми тремя изображенными на рис. 40, 1 - 3.
Метаморфозы каустик, движущихся в трехмерном пространстве, получаются сечениями больших (трехмерных) каустик в четырехмерном пространстве-времени трехмерными изохронами, Эти метаморфозы изображены на рис. 44 и 45.
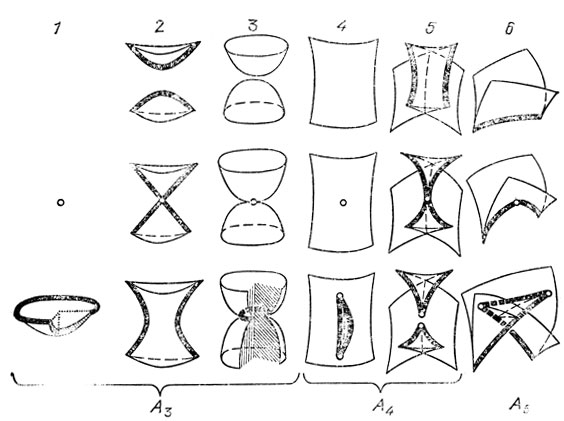
Рис. 44. Типичные переустройки каустик в трехмерном пространстве: серия А
Одна из этих метаморфоз (1) описывает рождение новой каустики "из воздуха". Мы видим, что вновь родившаяся каустика имеет вид блюдца с заостренными краями. Через время t после рождения длина и ширина блюдца порядка √t, глубина порядка t, а толщина порядка t √t.
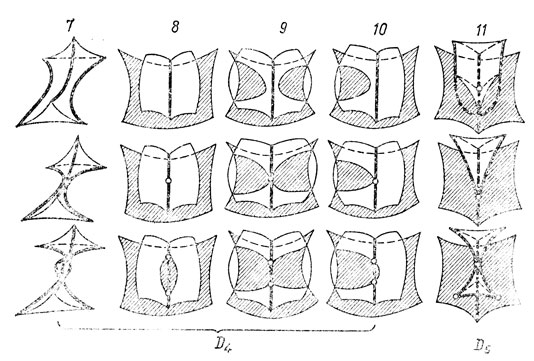
Рис. 45. Типичные перестройки каустик в трехмерном пространстве: серия D
Каустика может сделаться видимой, если на пути светового пучка имеется рассеивающая среда (пыль, туман). В. М, Закалюкин предположил, что каустики этого вида наблюдатели описывают как летающие блюдца.
Ребра возврата движущихся в трехмерном пространстве каустик заметают поверхность бикаустики. Особенности бикаустик общего положения, соответствующих различным метаморфозам рис. 44 и 45, изображены на рис. 46.
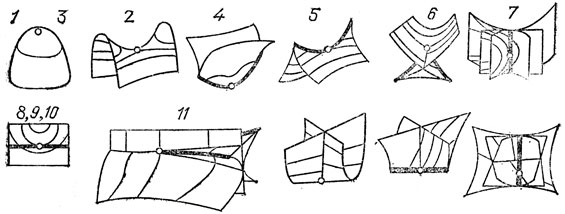
Рис. 46. Типичные особенности бикаустик
Как известно, лучи описывают распространение волн (скажем, световых) лишь в первом приближении; при более точном волновом описании появляется новый существенный параметр - длина волны (лучевое описание пригодно лишь в случае, когда эта длина мала по сравнению с характерным геометрическим размером системы).
Интенсивность света вблизи каустики больше, а вблизи ее особенностей еще больше. Коэффициент усиления оказывается пропорциональным l-α, где l - длина волны, а показатель α - рациональное число, зависящее от характера особенности. Для простейших особенностей значения α таковы:
| Каустика | Ребро возврата | Ласточкин хвост | Пирамида | Кошелек |
| 1/6 | 1/4 | 3/10 | 1/3 | 1/3 |
Таким образом, ярче всего светятся точечные особенности тина пирамиды и кошелька. В случае движущейся каустики в отдельные моменты времени могут возникать более яркие особенности* А5, D5 (см. рис. 44, 45, α = 1/3 для А5, 3/8 для D5).
*(Все перечисленные особенности классифицируются по типам Ak, Dk, о которых подробнее рассказано выше.)
Если свет настолько интенсивен, что способен разрушать среду, то разрушение начнется в точках наибольшей яркости, поэтому показатель α определяет зависимость интенсивности разрушающего среду света от частоты.
Аналогичная описанной выше классификация особенностей каустик и волновых фронтов проведена в многомерных пространствах до размерности 10 (В. М, Закалюкин) существенный параметр - длина волны (лучевое описание пригодно лишь в случае, когда эта длина мала по сравнению с характерным геометрическим размером системы).
Интенсивность света вблизи каустики больше, а вблизи ее особенностей еще больше. Коэффициент усиления оказывается пропорциональным l-α, где l - длина волны, а показатель α - рациональное число, зависящее от характера особенности. Для простейших особенностей значения α таковы:
| Каустика | Ребро возврата | Ласточкин хвост | Пирамида | Кошелек |
| 1/6 | 1/4 | 3/10 | 1/3 | 1/3 |
Таким образом, ярче всего светятся точечные особенности типа пирамиды и кошелька. В случае движущейся каустики в отдельные моменты времени могут возникать более яркие особенности* A5, D5 (см. рис. 44, 45, α = 1/3 для А5, 3/8 для D5).
*(Все перечисленные особенности классифицируются по типам Аk, Dk, о которых, подробнее рассказано ниже.)
Если свет настолько интенсивен, что способен разрушать среду, то разрушение начнется в точках наибольшей яркости, поэтому показатель α определяет зависимость интенсивности разрушающего среду света от частоты.
Аналогичная описанной выше классификация особенностей каустик и волновых фронтов проведена в многомерных пространствах до размерности 10 (В, М. Закалюкин).
Предсказания теорией особенностей геометрии каустик, фронтов и их перестроек получили полное подтверждение в экспериментах, и сейчас даже кажется странным, почему эта теория не была построена лет двести назад. Дело, однако, в том, что соответствующий математический аппарат не тривиален* и связан с такими разделами математики, как классификации простых алгебр Ли и кристаллографических групп Кокстера, с теорией кос, теорией ветвления интегралов, зависящих от параметров, и т. д - он даже связан (довольно таинственным образом) с классификацией правильных многогранников в трехмерном евклидовом пространстве.
*(Первоначальное доказательство теоремы Уитни, о которой мы начали, занимало около 40 страниц; хотя окончательные геометрические результаты теории особенностей легко могут быть понятны и использованы, доказательства продолжают оставаться сложными.)
Катастрофисты пытаются избежать серьезной математики. Например, в составленной К. Знманом в 1980 г. обширной библиографии по теории катастроф опущены ссылки на математические работы, вышедшие после 1976 г. Таким образом, катастрофисты продолжают попытки экспериментально нащупать ответы в задачах, давно решенных математиками. Например, в работе 1980 г. о ветровых полях и движении льда можно найти полуудачные попытки угадать список метаморфоз каустик в трехмерном пространстве (см. рис. 44, 45), опубликованный математиками еще в 1976 г.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'