7. Особенности границы устойчивости и принцип хрупкости хорошего

Рассмотрим положение равновесия системы, зависящей от нескольких параметров, и предположим, что (в некоторой области изменения параметров) это положение равновесия не бифурцирует.

Будем изображать систему, соответствующую какому-либо значению параметров, точкой на оси значений параметра (на плоскости, если параметров два, в пространстве параметров, если их три, и т. д.).

Изучаемая область в пространстве параметров разобьется тогда на две части в соответствии с тем, устойчиво или нет положение равновесия. Мы получаем таким образом на плоскости (в пространстве) параметров область устойчивости (составленную значениями параметров, при которых равновесие устойчиво), область неустойчивости и разделяющую их границу устойчивости.

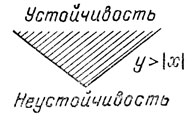
Рис. 30. Типичная особенность границы двумерной области устойчивости

В соответствии с общей стратегией Пуанкаре (см. п. 5) мы ограничимся семействами систем, зависящих от параметров общим образом. Оказывается, граница устойчивости может иметь особенности, которые не исчезают при малом шевелении семейства.

На рис. 30 изображены все особенности границы устойчивости положений равновесия в общих двупараметрических семействах эволюционных систем (с фазовым пространством любой размерности), на рис. 31 - в трехпараметрических. Формулы на рисунках описывают область устойчивости (при подходящем выборе координат на плоскости или в пространстве параметров, вообще говоря, криволинейных).

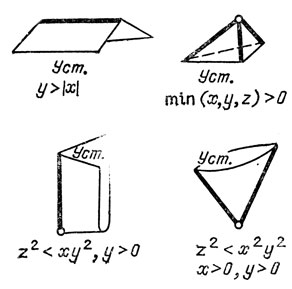
Рис. 31. Типичные особенности границ трехмерных областей устойчивости

Заметим, что область устойчивости во всех случаях располагается "углами наружу", вклиниваясь "зияющими вершинами" в область неустойчивости. Таким образом, для системы, принадлежащей особой части границы устойчивости, при малом изменении параметров более вероятно попадание в область неустойчивости, чем в область устойчивости. Это проявление общего принципа, согласно которому все хорошее (например, устойчивость) более хрупко, чем плохое.

По-видимому, все хорошие объекты удовлетворяют нескольким требованиям одновременно, плохим же считается объект, обладающий хотя бы одним из ряда недостатков.

В случае четырех параметров к перечисленным выше особенностям границы добавляются еще две.

При увеличении числа параметров число типов особенностей границы устойчивости семейства общего положения быстро растет, однако, как доказал Л. В. Левантовский, оно остается конечным (с точностью до гладких замен параметров) при любом конечном числе параметров, сохраняется и принцип хрупкости.