6. Потеря устойчивости равновесных и автоколебательных режимов

Потеря устойчивости состояния равновесия при изменении параметра не обязательно связана с бифуркацией самого состояния равновесия: оно может терять устойчивость не только сталкиваясь с другим, но и самостоятельно.

Соответствующая перестройка фазового портрета на плоскости изображена на рис. 16. Возможны два варианта.

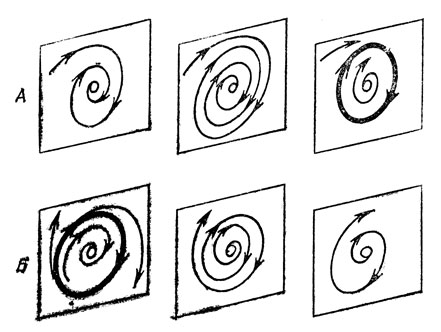
Рис. 16. Бифуркация рождения цикла

А. При изменении параметра из положения равновесия рождается предельный цикл (радиуса порядка √ε, когда значение параметра отличается от бифуркационного на ε). Устойчивость равновесия переходит к циклу, само же равновесие становится неустойчивым.

Б. В положении равновесия умирает неустойчивый предельный цикл; область притяжения положения равновесия уменьшается с ним до нуля, после чего цикл исчезает, а его неустойчивость передается равновесному состоянию.

А. Пуанкаре заметил, а А. А. Андронов и его ученики еще до войны (в 1939 г.) доказали, что, кроме описанной выше (п. 5) потери устойчивости положений равновесия сливающихся с неустойчивыми, и только что описанных способов потери устойчивости типа А или Б в общих однопараметрических семействах систем с двухмерным фазовым пространством никаких иных видов потери устойчивости не встречается. Позже было доказано, что и в системах с фазовым пространством большей размерности потеря устойчивости положений равновесия при изменении одного параметра происходит каким-либо из описанных выше способов (по направлениям всех дополнительных осей координат при изменении параметра равновесие остается притягивающим).

Если наше положение равновесия - установившийся режим в реальной системе, то при изменении параметра в случаях А и Б наблюдаются следующие явления.

А. После потери устойчивости равновесия установившимся режимом оказывается колебательный периодический режим (рис. 17); амплитуда колебаний пропорциональная квадратному корню из закритичности (отличия параметра от критического значения, при котором равновесие теряет устойчивость).

Этот вид потери устойчивости называется мягкой потерей устойчивости, так как устанавливающийся колебательный режим при малой закритичности мало отличается от состояния равновесия.

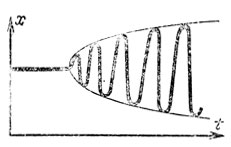
Рис. 17. Мягкая потеря устойчивости равновесия

Б. Перед тем как установившийся режим теряет устойчивость, область притяжения этого режима становится очень малой, и всегда присутствующие случайные возмущения выбрасывают систему из этой области еще до того, как область притяжения полностью исчезает.

Рис. 18. Жесткая потеря устойчивости равновесия

Этот вид потери устойчивости называется жесткой потерей устойчивости. При этом система уходит со стационарного режима скачком (см. рис. 18) и перескакивает на иной режим движения. Этот режим может быть другим устойчивым стационарным режимом, или устойчивыми колебаниями, или более сложным движением.

Установившиеся режимы движения получили в последние годы название аттракторов, так как они "притягивают" соседние режимы (переходные процессы), [Аттрактор, т. е. притягатель, - это притягивающее множество в фазовом пространстве. Аттракторы, отличные от состояний равновесий и строго периодических колебаний, получили название странных аттракторов и связываются с проблемой турбулентности.]

Существование аттракторов с экспоненциально расходящимися фазовыми кривыми на них и устойчивость такого рода явлений были установлены в самом начале шестидесятых годов в работах С. Смейла, Д. В. Аносова и Я. Г. Синая по структурной устойчивости динамических систем.

Независимо от этих теоретических работ метеоролог Лоренц в 1963 г. описал наблюдавшийся им в численных экспериментах по моделированию конвекции аттрактор в трехмерном фазовом пространстве с разбегающимися по нему в разные стороны фазовыми кривыми (рис. 19) и указал на связь этого явления с турбулентностью.

Рис. 19. Хаотический аттрактор

В работах Аносова и Синая экспоненциальное разбегание было установлено, в частности, для движения материальной точки по поверхности отрицательной кривизны

(пример такой поверхности - седло). Первые применения теории экспоненциального разбегания к изучению гидродинамической устойчивости опубликованы в 1966 г.

Движение жидкости можно описать как движение материальной точки по искривленной бесконечномерной поверхности. Кривизна этой поверхности по многим направлениям отрицательна, что приводит к быстрому разбеганию траекторий, т. е. к плохой предсказуемости течения по начальным условиям. В частности, из этого вытекает практическая невозможность долгосрочного динамического прогноза погоды: для предсказания всего на 1 - 2 месяца вперед нужно знать начальные условия с погрешностью 10^-5 от погрешности предсказания.

Вернемся, однако, к режиму, установившемуся после потери устойчивости равновесного состояния, и предположим, что этот режим - странный аттрактор (т. е. не равновесие и не предельный цикл).

Переход системы на такой режим означает, что в ней наблюдаются сложные непериодические колебания, детали которых очень чувствительны к малому изменению начальных условий, в то время как усредненные характеристики режима устойчивы и не зависят от начального условия (при его изменении в некоторой области). Экспериментатор, наблюдающий за движением такой системы, назвал бы его турбулентным. По-видимому, неупорядоченные движения жидкости, наблюдаемые при потере устойчивости ламинарного течения с увеличением числа Рейнольдса (т. е. с уменьшением вязкости), математически описываются именно такими сложными аттракторами в фазовом пространстве жидкости. Размерность этого аттрактора, по-видимому, конечна при любом числе Рейнольдса (для двухмерных течений жидкости Ю. С. Ильяшенко, М. И. Вишик и А. В. Бабин недавно получили оценку этой размерности сверху величиной порядка Rе⁴), но стремится к бесконечности при Re → ∞.

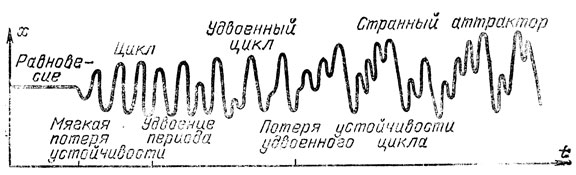
Рис. 20. Сценарий хаотизации

Переход от устойчивого состояния равновесия процесса ("ламинарного течения жидкости") к странному аттрактору ("турбулентности") может совершаться как скачком (при жесткой или катастрофической потере устойчивости), так и после мягкой потери устойчивости (рис. 20). В последнем случае родившийся цикл сам теряет устойчивость. Потеря устойчивости цикла в общем однопараметрическом семействе систем возможна несколькими способами: 1) столкновение с неустойчивым циклом (рис. 21), 2) удвоение (рис. 22), 3) рождение или смерть тора (рис. 23) (в терминологии Андронова: с цикла слезает шкура). Детали последних процессов зависят от резонансов между частотами движения вдоль меридиана тора и вдоль его оси, т. е. от того, будет ли отношение этих частот рациональным или иррациональным числом. Интересно, что рациональные числа со знаменателем 5 и больше ведут себя практически как иррациональные.

Рис. 21. Гибель аттрактора-цикла

Поведение фазовых кривых, близких к циклу, можно приближенно описывать при помощи эволюционнсго процесса, для которого цикл является положением равновесия. Возникающие таким образом приближенные системы на сегодняшний день исследованы для всех случаев, кроме случаев, близких к сильному резонансу с отношением частот 1 : 4 (Р. И. Богданов, Э. И. Хорозов). На рис. 24 изображены перестройки семейства фазовых кривых приближенной системы, соответствующие перестройкам расположения фазовых кривых в окрестности цикла; предполагается, что потеря устойчивости происходит вблизи резонанса 1 : 3. На рис. 25 изображена одна из возможных последовательностей событий вблизи резонанса 1 : 4. Основные результаты об этом резонансе получены не строгими математическими рассуждениями, а комбинированием догадок и вычислительных экспериментов на ЭВМ (Ф. С. Березовская и А. И. Хибник, А. И. Нейштадт).

Рис. 22. Удвоение цикла-аттрактора

Изложенная выше теория Пуанкаре - Андронова потери устойчивости состояний равновесия имеет так много приложений во всех областях теории колебаний (как систем с конечным числом степеней свободы, так и сплошных сред), что нет никакой возможности их здесь перечислить: механические, физические, химические, биологические и экономические системы теряют устойчивость на каждом шагу.

Рис. 23. Бифуркация рождения тора вблизи цикла

В работах по теории катастроф мягкая потеря устойчивости положения равновесия обычно называется бифуркацией Хопфа (отчасти по моей "вине", так как, рассказывая о теории Пуанкаре - Андронова Р. Тому в 1965 г., я особенно подчеркивал работу Э. Хопфа, перенесшего часть этой теории на многомерный случай).

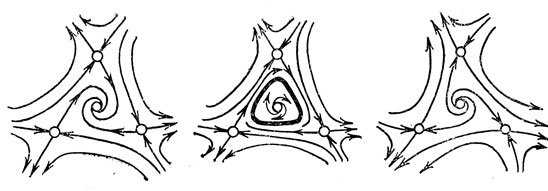
Рис. 24. Бифуркация коразмерности 2 вблизи резонанса 1 : 3

В теории бифуркаций, как и в теории особенностей, основные результаты и приложения получены независимо от теории катастроф. Несомненной заслугой теории катастроф является введение термина аттрактор и широкая пропаганда знаний о бифуркациях аттракторов. Разнообразные аттракторы обнаружены теперь во всех областях теории колебаний; высказывалась, например, гипотеза, что различные фонемы речи - это различные аттракторы звукообразующей динамической системы.

Рис. 25. Вариант бифуркации коразмерности 2 вблизи резонанса 1 : 4

При медленном изменении параметра наблюдается качественно новое явление затягивания потери устойчивости (рис. 26).

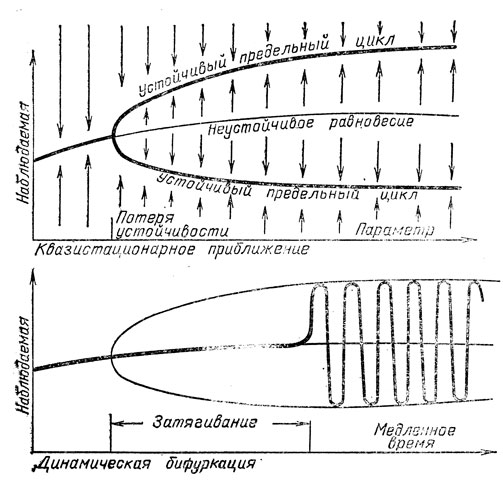
Рис. 26. Затягивание потери устойчивости при динамической бифуркации

После того как параметр прошел через бифуркационное значение, соответствующее рождению цикла, т. е. мягкому возникновению автоколебаний, система остается в окрестности потерявшего устойчивость состояния равновесия еще некоторое время, за которое параметр успевает измениться на конечную величину. И лишь затем система скачком переходит на родившийся в момент бифуркации автоколебательный режим, так что потеря устойчивости кажется жесткой.

Интересно, что этот эффект - особенность динамической бифуркации - имеет место только в аналитических системах, В бесконечно-дифференцируемом случае величина затягивания потери устойчивости, вообще говоря, стремится к нулю при уменьшении скорости изменения параметра.

Затягивание в модельном примере описано Шишковой в 1973 г. Доказательство того, что это явление имеет место во всех типичных аналитических системах с медленно меняющимся параметром, было получено в 1985 г. А. И. Нейштадтом.

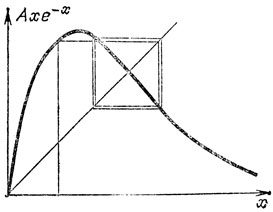
Рис. 27. Колебания численности популяции в простейших мальтузианской модели с учетом конкуренции

Известно, что улов горбуши колеблется с периодом два года. Исследование экологических моделей, призванных объяснить эти колебания, привело А. П. Шапиро (1974) и затем Р. Мея к экспериментальному открытию каскадов удвоений периода: последовательные бифуркации удвоения быстро следуют одна за другой, так что на конечный отрезок изменения параметра приходится бесконечное число удвоений. Это явление наблюдается, например, для простейшей модели мальтузианского размножения с конкуренцией - для отображения х → Ахе^-х (рис. 27). Здесь множитель е^-х, уменьшающий коэффициент мальтузианского размножения А при увеличении размера популяции х, учитывает конкуренцию. При малых значениях параметра А устойчива неподвижная точка х = 0 (популяция вымирает). При больших значениях А аттрактором последовательно становятся ненулевая неподвижная точка (бифуркация А₀), цикл периода 2, рис. 27, как для горбуши (бифуркация удвоения, А₁) периода 4 (А₂) и т. д. (рис. 28).

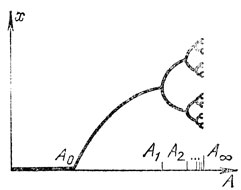
Рис. 28. Каскад удвоений периода

Анализируя этот экспериментальный материал, М. Фейгенбаум (1978) обнаружил замечательное явление универсальности каскадов удвоений. Последовательность значений параметра, соответствующих последовательным удвоениям, асимптотически ведет себя как геометрическая прогрессия. Знаменатель прогрессии

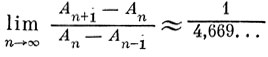
является универсальной (не зависящей от конкретной системы) постоянной, вроде чисел π или ε. Такие же каскады удвоений предельных циклов наблюдаются и в типичных эволюционных системах, описываемых зависящими от параметра дифференциальными уравнениями.

В отличие от удвоения периода, утроение является явлением коразмерности два. Каскады утроений (и других увеличений периода) становятся типичными не в однопараметрических, а в двупараметрических семействах систем. В этих случаях универсальные показатели оказываются комплексными.

В теории двупараметрических бифуркаций за последние годы достигнуты значительные успехи, в частности, Г. Жолондеком к 1987 г. решены давно стоявшие задачи о числе предельных циклов, рождающихся из нулевого положения равновесия в системах типа Лотка - Вольтерра (рис. 10), описываемых касающимися сторон угла векторными полями на плоскости.

Однако задача о бифуркациях в системе

к которой сводится исследование потери устойчивости автоколебаний в единственном оставшемся не исследованным случае коразмерности 2, все еще не поддается усилиям математиков. На плоскости комплексного параметра А выделено 48 областей (рис. 29), в которых бифуркации при обходе малого комплексного параметра ε вокруг нуля происходят по-разному. (Не доказано даже, что полное число таких областей конечно, хотя предполагается, что их всего 48.)

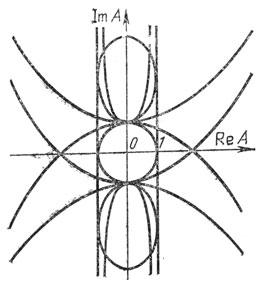
Рис. 29. Сорок восемь типов бифуркаций коразмерности 2 при резонансе 1 : 4

Еще недавно всякий экспериментатор, обнаружив, скажем, в химической реакции сложные апериодические колебания, отказывался от их исследования, ссылаясь на нечистоту эксперимента, случайные внешние воздействия и т. п. Сейчас уже многим ясно, что эти сложные колебания могут быть связаны с самим существом дела, могут определяться основными уравнениями задачи, а не случайными внешними воздействиями; они могут и должны изучаться наравне с классическими стационарными и периодическими режимами протекания процессов.