5. Бифуркации положений равновесия

Эволюционный процесс математически описывается векторным полем в фазовом пространстве. Точка фазового пространства задает состояние системы. Приложенный в этой точке вектор указывает скорость изменения состояния.

В некоторых точках вектор может обращаться в нуль. Такие точки называются положениями равновесия (состояние не меняется с течением времени). На рис. 10 изображено фазовое пространство системы, описывающей взаимоотношение хищника и жертвы (скажем, щук и карасей). Фазовое пространство - положительный квадрант плоскости. По оси абсцисс отложено число карасей, по оси ординат - щук. Точка Р - положение равновесия. Точка А соответствует равновесному количеству карасей при количестве щук, меньшем равновесного. Видно, что с течением времени в системе устанавливаются колебания; равновесное состояние рис. 10 неустойчиво. Установившиеся колебания изображаются замкнутой кривой на фазовой плоскости. Эта кривая называется предельным циклом.

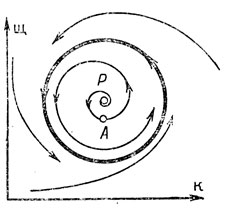
Рис. 10. Фазовая плоскость модели хищник - жертва

Кривые в фазовом пространстве, образованные последовательными состояниями процесса, называются фазовыми кривыми. В окрестности точки, не являющейся положением равновесия, разбиение фазового пространства на фазовые кривые устроено так же, как разбиение на параллельные прямые: семейство фазовых кривых можно превратить в семейство параллельных прямых гладкой заменой координат. В окрестности положения равновесия картина сложнее. Как показал еще А. Пуанкаре, поведение фазовых кривых в окрестности положения равновесия на фазовой плоскости в системе общего положения такое, как изображено на рис. 11. Все более сложные случаи превращаются в указанные при общем малом изменении системы.

Рис. 11. Типичные фазовые портреты в окрестности точки равновесия

Системы, описывающие реальные эволюционные процессы, как правило, общего положения. Действительно, такая система всегда зависит от параметров, которые никогда не бывают известны точно. Малое общее изменение параметров превращает систему необщего положения в систему общего положения.

Таким образом, все более сложные, чем указанные выше, случаи, вообще говоря, не должны встречаться в природе, и их на первый взгляд можно не рассматривать. Эта точка зрения обесценивает большую часть теории дифференциальных уравнений и вообще математического анализа, где традиционно основное внимание уделяется малоценным, но трудным для исследования случаям не общего положения.

Дело, однако, обстоит совсем иначе, если нас интересует не индивидуальная система, а система, зависящая от одного или нескольких параметров. Действительно, рассмотрим пространство всех систем (рис. 12), разделенное на области, образованные системами общего положения. Поверхности раздела отвечают вырожденным системам; при малом изменении параметров вырожденная система становится невырожденной. Однопараметрическое семейство систем изображается на рис. 12 кривой. Эта кривая может трансверсально (под ненулевым углом) пересекать границу раздела разных областей невырожденных систем.

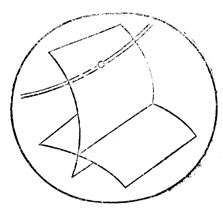
Рис. 12. Однопараметрическое семейство как кривая в пространстве систем

Таким образом, хотя при каждом индивидуальном значении параметра систему малым шевелением можно превратить в невырожденную, этого нельзя сделать одновременно при всех значениях параметра: всякая кривая, близкая к рассматриваемой, пересекает границу раздела при близком значении параметра (вырождение, устраненное малым шевелением при данном значении параметра, вновь возникает при некотором близком значении).

Итак, вырожденные случаи неустранимы, если рассматривается не индивидуальная система, а целое семейство. Если семейство однопараметрическое, то неустранимы лишь простейшие вырождения, изображаемые границами коразмерности один (т. е. задающимися одним уравнением) в пространстве всех систем. От более сложных вырожденных систем, образующих множество коразмерности два в пространстве всех систем, можно избавиться малым шевелением однопараметрического семейства.

Если мы интересуемся двупараметрическим семейством, то можно не рассматривать вырожденных систем, образующих множество коразмерности три и т. д.

Тем самым возникает иерархия вырождений по коразмерностям и стратегия их исследования: вначале следует изучать случаи общего положения, затем вырождения коразмерности один, затем - два и т. д. При этом исследование вырожденных систем не должно ограничиваться изучением картины в момент вырождения, но должно включать описание перестроек, происходящих, когда параметр, меняясь, проходит через вырожденное значение.

Изложенные выше общие соображения принадлежат А. Пуанкаре и применимы не только к исследованию положений равновесия эволюционных систем, но к большей части всего математического анализа. Хотя они были высказаны уже сто лет назад, успехи в реализации намеченной А. Пуанкаре программы теории бифуркаций остаются в большинстве областей анализа довольно скромными, отчасти в силу больших математических трудностей, отчасти же вследствие психологической инерции и засилья аксиоматико-алгебраического стиля.

Вернемся, однако, к положениям равновесия эволюционных систем. К настоящему времени решенным можно считать лишь вопрос о перестройках фазовых кривых при бифуркациях положений равновесия в однопараметрических семействах общего положения; уже случай двух параметров выходит за рамки возможностей сегодняшней науки.

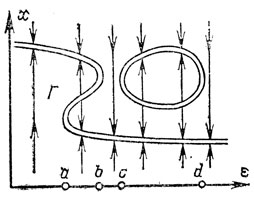
Рис. 13. Кривая равновесий однопараметрического семейства систем

Результаты исследования общего однопараметрического семейства суммированы на рис. 13 - 18. На рис. 13 изображено однопараметрическое семейство эволюционных процессов с одномерным фазовым пространством (по оси абсцисс отложено значение параметра ε, по оси ординат - состояние процесса х).

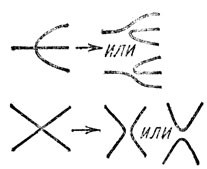
Рис. 14. Превращение нетипичных бифуркаций в типичные при малом шевелении семейства

Для однопараметрического семейства общего положения равновесия при всевозможных значениях параметра образуют гладкую кривую (Г на рис. 13, в более общем случае размерность многообразия состояний равновесия равна числу параметров). В частности, это означает, что изображенные на рис. 14 слева бифуркации в семействе общего положения не встречаются: при малом изменении семейства Г превращается в гладкую кривую одного из изображенных на рис. 14 справа типов^*.

^*(Под "типом" здесь понимается класс эквивалентности с точностью до диффеоморфизма плоскости, а не с точностью расслоенного диффеоморфизма (расслоенный диффеоморфизм - это семейство диффеоморфизмов фазового пространства, зависящих от параметра, сопровождаемых диффеоморфной заменой параметра).)

Проектирование кривой Г на ось значений параметра в случае однопараметрического семейства имеет лишь особенности типа складки (при большем числе параметров появляются и более сложные особенности теории Уитни: например, в общих двупараметрических семействах проектирование поверхности равновесий Г на плоскость значений параметров может иметь точки сборки, где сливаются три положения равновесия).

Таким образом, при изменении параметра выделяются особые или бифуркационные значения параметра (критические значения проекции, a, b, с, d на рис. 13). Вне этих значений положения равновесия гладко зависят от параметров. При подходе параметра к бифуркационному значению положение равновесия "умирает", слившись с другим (или же "из воздуха" рождается пара положений равновесия).

Из двух рождающихся (или умирающих) вместе положений равновесия одно устойчиво, другое неустойчиво.

В момент рождения (или смерти) оба положения равновесия движутся с бесконечной скоростью: когда значение параметра отличается от бифуркационного на ε, оба близких положения равновесия удалены друг от друга на расстояние порядка √ε.

На рис. 15 изображена перестройка семейства фазовых кривых на плоскости в общем однопараметрическом семействе. Устойчивое положение равновесия ("узел") сталкивается при изменении параметра с неустойчивым ("седлом"), после чего оба исчезают. В момент слияния на фазовой плоскости наблюдается картина необщего положения ("седло-узел").

На рис. 15 видно, что перестройка, в сущности, одномерная: вдоль оси абсцисс происходят те же явления, что на оси х на рис. 13, а вдоль оси ординат перестройки нет вовсе. Таким образом, перестройка через седло - узел получается из одномерной перестройки "надстраиванием" оси ординат. Оказывается, вообще все перестройки положений равновесия в общих однопараметрических системах получаются из одномерных перестроек аналогичным надстраиванием.

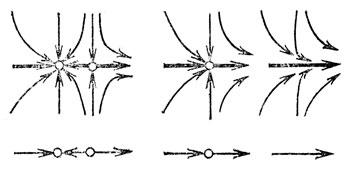
Рис. 15. Седло-узел: типичная локальная бифуркация в одно- параметрическом семействе

Если устойчивое положение равновесия описывает установившийся режим в какой-либо реальной системе (скажем, экономической, экологической или химической), то при его слиянии с неустойчивым положением равновесия система должна совершить скачок, перескочив на совершенно другой режим: при изменении параметра равновесное состояние в рассматриваемой окрестности исчезает. Скачки этого рода и привели к термину "теория катастроф".