Дифференциальное и интегральное исчисления

105. Составьте производные от функций 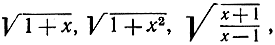исходя непосредственно из определения, а затем преобразовывая разностное отношение таким образом, чтобы не представило труда вычислить предел при х→x₁ (см. стр. 453-455).

106. Докажите, что функция 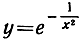с дополнительным условием y = 0 при х = 0 имеет производные всех порядков, равные нулю, в точке х = 0.

107. Установите, что функция упражнения 106 не разлагается в ряд Тейлора в точке х = 0 (см. стр. 514).

108. Найти точки перегиба (f"(x) = 0) кривых

109. Покажите, что если f" (x) - полином с n различными корнями x₁, x₂, ..., x_n, то

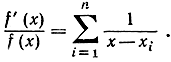
^* 110. Исходя из определения интеграла как предела суммы, доказать, что при n→∞

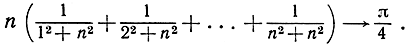
^* 111. Таким же образом доказать, что

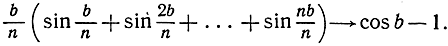
112. Нарисуйте рис. 276 на клетчатой бумаге в крупном масштабе и затем, подсчитывая маленькие квадратики, попадающие в заштрихованную область, найдите приближенное значение n.

113. Воспользуйтесь формулой (7) на стр. 476, чтобы вычислить к с погрешностью, не превышающей 0,01.

114. Докажите, что е^πi = -1 (см. стр. 516).

115. Данная замкнутая кривая увеличивается, расширяясь в отношении 1:х. Пусть L(x) и А(х) обозначают длину расширенной кривой и L (х) ограниченную ею площадь. Покажите, что 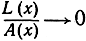при х→∞ и что даже 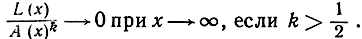. Проверьте это для окружности, квадрата и ^*эллипса. (Площадь - более высокого порядка возрастания, чем длина кривой. См. стр. 506 и далее.)

116. Показательная функция часто встречается в следующих комбинациях:

называемых соответственно гиперболическим синусом, гиперболическим косинусом и гиперболическим тангенсом. Эти функции обладают многими свойствами, напоминающими свойства тригонометрических функций. Они связаны с гиперболой u² - v² = 1 также, как тригонометрические функции с окружностью u² + v² = 1. Читателю предлагается проверить следующие формулы и сопоставить их с тригонометрическими формулами:

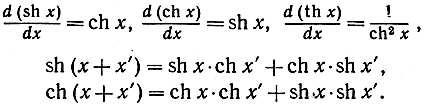
Обратные функции таковы:

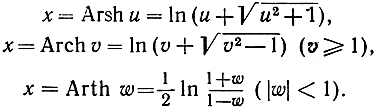
Их производные имеют вид:

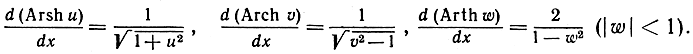
117. Уясните себе аналогию между гиперболическими и тригонометрическими функциями на основе формулы Эйлера.

* 118. Выведите простые формулы для сумм

и

аналогично формулам, выведенным в упражнении 14 для тригонометрических функций.